第2章 线性代数
深度学习中允许矩阵和向量相加 广播:隐式地复制n列向量$b$ $C=A+b, 其中C_{i,j} = A_{i,j} + b_{j}$ 即:向量$b$和矩阵$A$的每一行相加
Hadamard乘积:元素对应乘积 $A\bigodot B$
范数
范数是将向量映射到非负值的函数(可用于距离衡量) $L^{p}范数:||x||{p} = (\sum\limits{i}|x_{i}|^{p})^{\frac{1}{p}}$
二范数欧氏距离 平方$L^2$范数=$x^Tx$ 衡量向量大小,即点积 在原点增长十分缓慢
$L^1$范数注重0与非0元素差异
最大范数$L^\infty$:$||x||{\infty} = max{i}|x_{i}|$ 向量中具有最大增幅的元素的绝对值
矩阵大小(类$L^{2}$):Frobenius范数 $||x||{F} = \sqrt{\sum\limits{i,j}A^{2}_{i,j}}$
对角矩阵计算效率很高
奇异值分解SVD
分解矩阵以更好地分析矩阵的性质
复杂矩阵所代表的线性变换可由若干个简单矩阵所代表的线性变换组合起来,SVD是找到简单矩阵的方法
(类似于质数分解)
每一个实数矩阵都有一个奇异值分解;未必有特征分解
$A=UDV^{T}$
$左奇异向量:U_{m\times m}$
$对角矩阵D_{m\times n}:未必为方阵;对角线元素为A的奇异值$
$右奇异向量:V_{n\times n}$
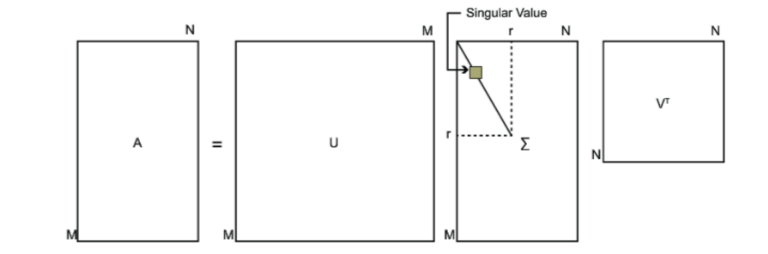
较大的奇异值便可以描述矩阵的多数特征
求解: 左奇异向量:$AA^{T}$的特征向量 右奇异向量:$A^{T}A$的特征向量 A的非零奇异值:$AA^{T}$特征值的平方根=$A^{T}A$特征值的平方根
M-P伪逆(Moore-Penrose广义逆)
伪逆是一种特殊的广义逆 对于非方阵而言,逆矩阵没有定义
为求解$Ax=y \Longrightarrow x=By$设计唯一映射A到B 称B为A的广义逆
若A的行数大于列数,方程可能无解 若A的行数小于列数,方程可能多个解
M-P伪逆计算:$A^{+} = VD^{+}U^{T}$ $U、D、V为A奇异值分解矩阵$ $D^{+}为对角阵D非零元素取倒数$ 即: \(A=U\begin{pmatrix}\Delta & 0 \\ 0 & 0\end{pmatrix} V^{T}\) \(A^{+}=V\begin{pmatrix}\Delta^{-1} & 0 \\ 0 & 0 \end{pmatrix}D^{T}\) 当A的行数大于列数,方程可能无解;此时通过伪逆得到的$x$使得$||Ax-y||{2}$二范数最小 当A的行数小于列数,通过伪逆得到的$x$为$x=A^{+}y$所有可行解中$||x||{2}$二范数最小的解
迹运算
$Tr(A)$矩阵对角元素和
| 另一种$Frobenius范数$计算方式:$ | A | _{F}=\sqrt{Tr(AA^{T)}}$ |
若多个矩阵相乘可得到方阵,则循环改变矩阵顺序不影响方阵的迹
标量的迹运算仍为自身:$a=Tr(a)$
行列式 等于矩阵特征值的乘积 行列式绝对值:衡量矩阵参与矩阵乘法后空间收缩情况 若为0则矩阵在至少某一维度完全收缩,体积为0 若为1则转换保持空间体积不变
PCA
对数据进行有损压缩
思想
假设$\mathbb{R}^{n}$空间中有$m$个点${x^{(1)}, …,x^{(m)}}$ 对于每个点$x^{(i)} \in \mathbb{R}^n$有一一映射$c^{(i)}\in \mathbb{R}^l$且$n>l$ 编码函数:$f(x)=c$ 解码函数:$x \approx g(f(x))=g(c)=Dc$ 为简化解码器令$g(·)$为矩阵$D \in \mathbb{R}^{n\times l}$ 设定D所有列向量都有单位范数且彼此正交(除非$l=n$,D不为正交矩阵)
*求解最优编码$c^{}$** 最小化原始输入向量$x$和重构向量$g(c^{*})$之间的距离 采用平方$L^2$范数衡量距离
\(\begin{aligned} C^{*} & =\mathop{\arg\min}\limits_{c}||x-g(c)||_2 \\ & = (x-g(c))^{T}(x-g(c))\\ &= x^{T}x-x^{T}g(c)-g(c)^{T}x+g(c)^{T}g(c) \\ &\because x^{T}g(c)、g(c)^{T}x为标量 \\ &= x^{T}x-2x^{T}g(c)+g(c)\end{aligned}\) 由于$x^{T}x$不依赖于$c$ \(\begin{aligned}c^{*} &= \mathop{\arg\min}\limits_{c} -2x^{T}g(c)+g(c)^{T}g(c) \\ &=\mathop{\arg\min}\limits_{c} -2x^{T}Dc+c^{T}D^{T}Dc \\ &\because D正交性和单位范数约束\\ &= \mathop{\arg\min}\limits_{c} -2x^{T}Dc+c^{T}I_{l}c \\ &= \mathop{\arg\min}\limits_{c} -2x^{T}Dc+C^{T}c \end{aligned}\) 最优化问题求解: \(\begin{aligned}\nabla_{c}(-2x^{T}Dc+c^{T}c)&=0 \\ -2D^{T}x+2c&=0 \\ c&=D^Tx\end{aligned}\) PCA算法非常高效:最优编码只需一个矩阵-向量乘法 $编码函数:f(x)=D^{T}x$ $解码函数:r(x)=g(f(x))=DD^{T}x$ $解码误差:x-r(x)$
编码矩阵D 最小化所有维数和所有点上的误差矩阵的Frobenius范数 \(\begin{aligned}D^{*}&=\mathop{\arg\min}\limits_{D} \sqrt{\sum\limits_{i,j}(x^{(i)}_{j}-r(x^{(i)})_{j})^{2}} \\ &s.t. D^{T}D=I_l\end{aligned}\) 首先考虑$l=1$,此时$D$为向量$d$ 重排问题,并记$X \in \mathbb{R}^{m\times n}, X_{i,:}=x^{(i)^T}$ \(\begin{aligned}d^{*}&=\mathop{\arg\min}\limits_{d} ||X-Xdd^{T}||^{2}_{F} \\ &s.t. d^Td=1\end{aligned}\) 首先忽略约束 \(\begin{aligned}原式&= \mathop{\arg\min}\limits_{d} Tr((X-Xdd^{T})^{T}(X-Xdd^{T}))\\&= \mathop{\arg\min}\limits_{d} Tr(X^{T}X)-Tr(X^{T}Xdd^{T})-Tr(dd^{T}X^{T}X)+Tr(dd^{T}X^{T}Xdd^{T}) \end{aligned}\) 排除与$d$无关项$Tr(X^{T}X)$ 由于循环改变迹运算中相乘矩阵的顺序不影响结果 \(\begin{aligned}原式&=\mathop{\arg\min}\limits_{d} -2Tr(X^{T}Xdd^T)+Tr(X^{T}Xdd^{T}dd^{T})\end{aligned}\) 考虑约束:$s.t.d^{T}d=1$ \(\begin{aligned}原式&=\mathop{\arg\min}\limits_{d} -2Tr(X^{T}Xdd^{T})+Tr(X^{T}Xdd^{T}) \\ &=\mathop{\arg\max}\limits_{d} Tr(X^{T}Xdd^{T})\\&=\mathop{\arg\max}\limits_{d} Tr(d^{T}X^{T}Xd)\\s.t.& d^Td=1\end{aligned}\) 通过特征分解求解优化问题:最优$d$是$X^{T}X$最大特征值对应的特征向量
更一般地,矩阵$D$由前$l$个最大特征值对应的特征向量组成