第3章 概率与信息论

频率派概率：概率直接与事件发生的频率相联系 贝叶斯概率：概率涉及确定性水平

离散型变量概率质量函数PMF 连续型变量概率密度函数PDF 累计分布函数CDF

符号“;”表示以x为参数 $u(x;a,b)$以$x$为自变量，$a$和$b$作为定义函数的参数

随机变量独立性$x\perp y$ 随机变量条件独立$x\perp y | z$

随机向量$x\in \mathbb{R}^{n}$的协方差矩阵$_{n\times n}$

$Cov(x){i,j} = Cov(x{i}, x_{j})$ 对角元素为方差

常用分布函数

正态分布：

1. 中心极限定理说明很多独立随机变量之和近似服从正态分布
2. 在具有相同方差的所有可能的概率分布中，正态分布在实数上具有最大的不确定性；即正态分布是对模型加入最少先验知识的分布

拉普拉斯分布Laplace Distribution 双指数分布：由两个指数分布组成 $Laplace(x;u,\gamma)= \frac{1}{2\gamma}e^{- \frac{|x-\mu|}{\gamma}}$ 允许在任一$\mu$处设置概率质量的峰值

狄拉克Dirac delta分布$\delta(x)$ 希望概率分布中所有质量集中在一个点上 $p(x)=\delta(x-\mu)$ 除0外所有点的值为0，积分为1

混合分布mixture distribution 混合分布由一些组件分布构成 ex.经验分布 混合分布使潜变量可测量

高斯混合模型Gaussian Mixture Model 组件$p(x|c=i)$是高斯分布的混合分布 GMM假设所有数据点都由具有位置参数的高斯分布混合而成 GMM用于将混合的分布还原为多个高斯分布【聚类】 查找集群、估计数据点属于集群的概率；对异常值稳健 可理解为概率模型 $P(y|\theta)=\sum\limits_{k=1}^{k}\alpha_{k}\phi(y|\theta_{k})$ $\alpha_{k}$为第$k$个高斯模型的权重 $\phi(y|\theta_{k})$是第$k$个高斯模型的概率密度函数含有均值方差两参数 GMM是概率密度万能近似器，任何平滑的概率密度都可借助足够多组间的GMM以任意精度逼近

logistic sigmoid函数 通常产生伯努利分布中的参数 $\sigma(x)=\frac{1}{1+e^{-x}}=\frac{e^{x}}{e^{x}+1}$ 性质： $\frac{d}{dx}\sigma(x)=\sigma(x)(1-\sigma(x))$ $1-\sigma(x)=\sigma(-x)$

softplus函数 用于产生正态分布的$\beta$和$\alpha$参数；取值范围$(0,\infty)$ $\zeta(x)=log(1+e^{x})$ 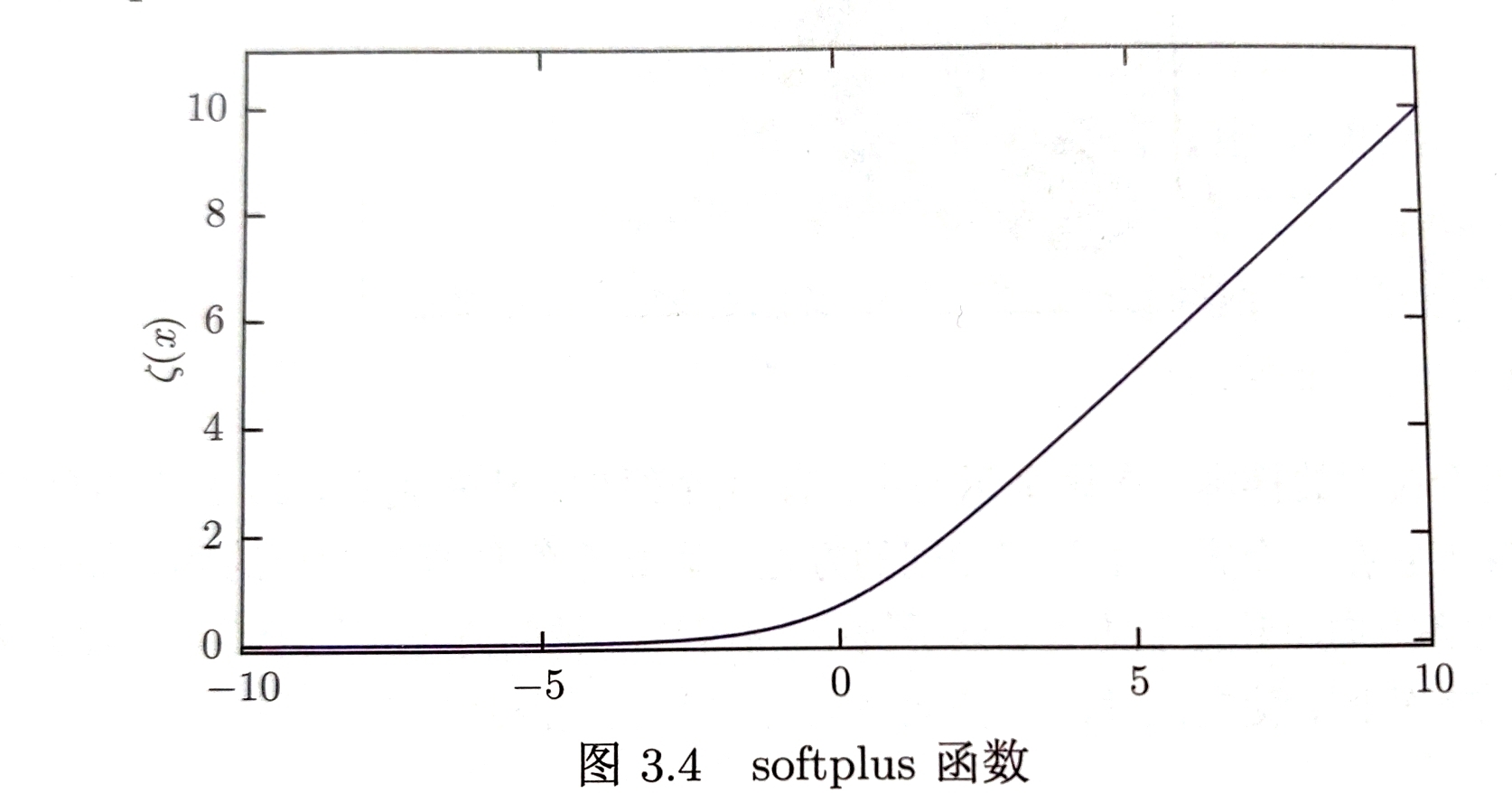softplus函数是正部函数$x^{+}=max{0,x}$的软化形式；$logistic$函数的积分 性质： $log\sigma(x)=-\zeta(-x)$ $\frac{d}{dx}\zeta(x)=\sigma(x)$ $\zeta(x)-\zeta(-x)=x$

测度论（少量细节）

零测度 零测度集在度量空间中不占有任何体积 用于描述非常微小的点集 几乎处处 在整个空间中除了测度为0的集合以外都成立

假设随机变量$x,y$满足$y=g(x)$，其中$g$是可逆、连续可微函数 $p_{y}(y)\neq p_{x}(g^{-1}(y))$ $\because$ 函数$g$会引起空间变形，使计算违背概率密度的定义 应为： $p_{y}(y)=p_{x}(g^{-1}(y))| \frac{\partial x}{\partial y}| \Longrightarrow p_{x}(x)=P_{y}(g(x)) |\frac{\partial g(x)}{\partial x}|$ 其中$|\frac{\partial g(x)}{\partial x}|$为Jacobian行列式$J_{i,j} = \frac{\partial x_{i}}{\partial y_{i}}$

信息论

对信号包含的信息多少进行量化

基本思想 常见事件提供较少信息，必然事件不提供信息 罕见事件提供更多信息 独立事件具有增量信息

事件$\mathbf{x}=x$的自信息：$I(x)=-logP(x)$ $log以e为底，I(x)单位为nat奈特；以2为底，单位为bit比特/香农$ 1奈特：以$\frac{1}{e}$概率观测到一个事件时获取的信息量

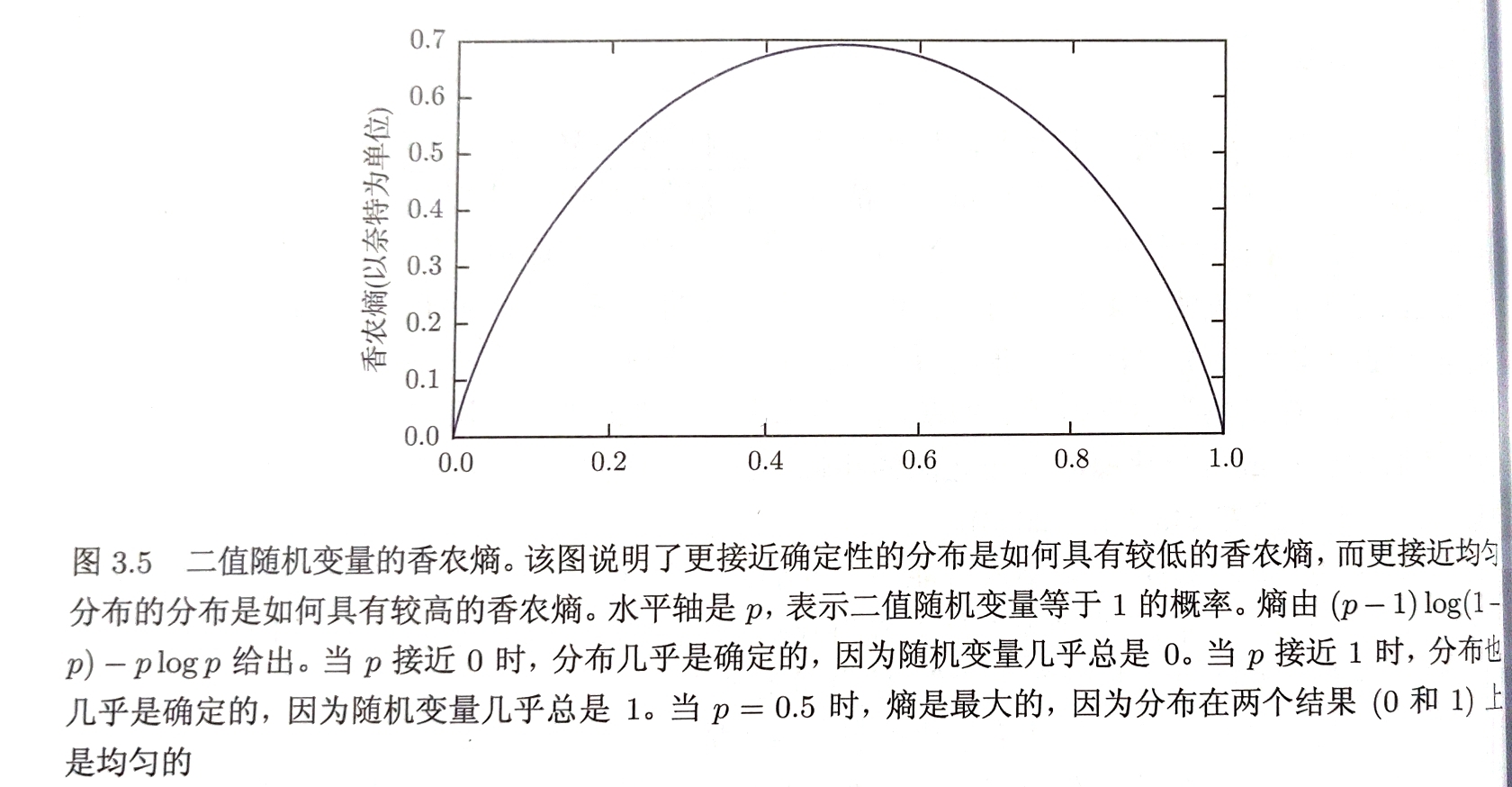
香农熵：对整个概率分布中不确定性总量进行量化 $H(x)=\mathbb{E}{x\backsim P}[I(x)]=-\mathbb{E}{x\backsim P}[logP(x)]$

一个分布的香农熵指遵循该分布的事件所产生的期望信息总量 当$x$为连续变量时，称香农熵为微分熵

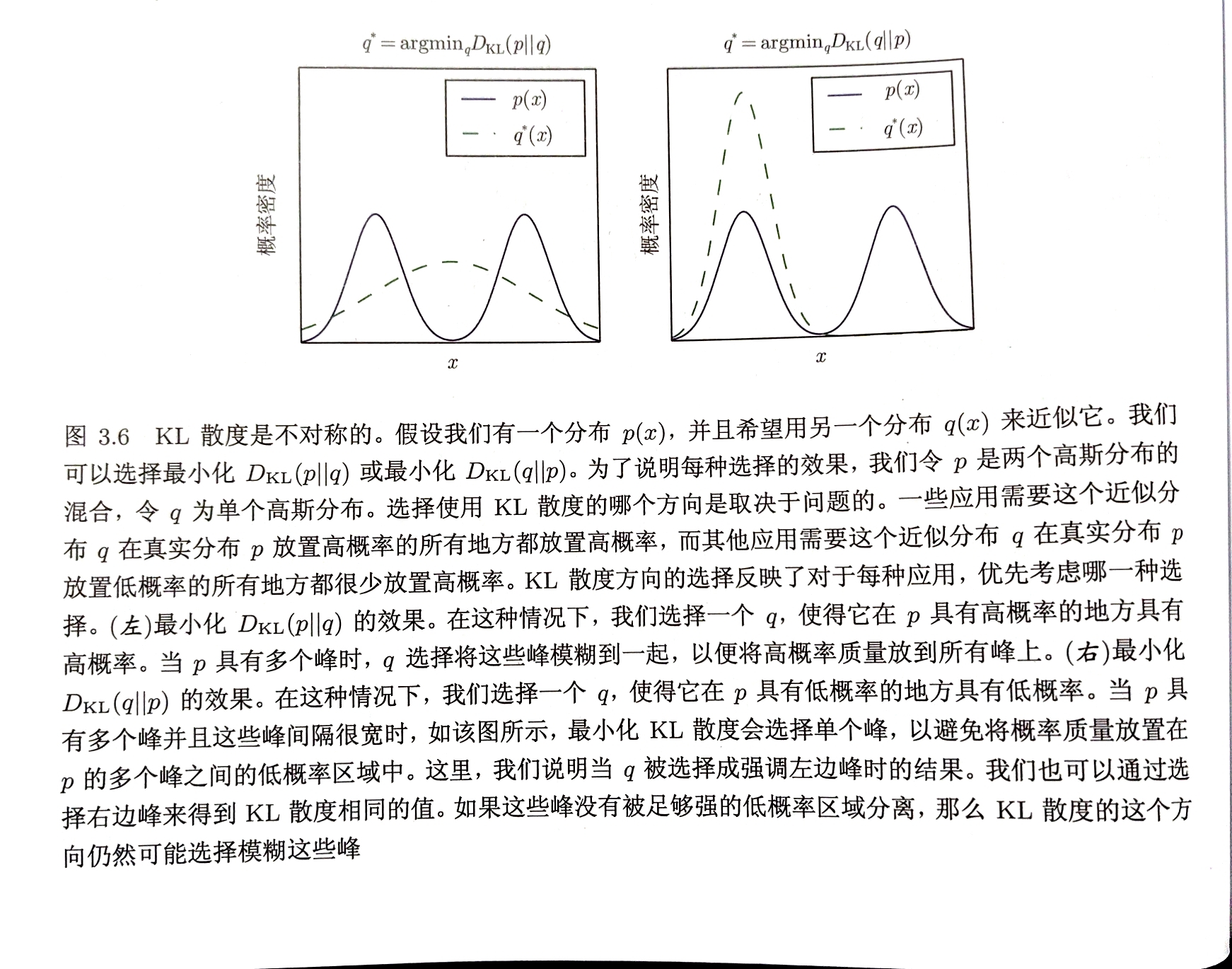
KL散度（相对熵、互熵）：对同一个随机变量$x$有两个单独的概率分布$P(x)$和$Q(x)$，KL单独用于衡量两个分布的差异 KL散度越小，分布的差异越小

KL散度非对称性、非负性 可用于衡量分布之间的“距离” 含义：当使用一种被设计成能使概率分布$Q$产生的消息的长度最小的编码，发送包含由概率分布$P$产生的符号的信息时，所需的额外信息量

交叉熵 $H(P,Q)=H(P)+D_{KL}(P||Q)=-\mathbb{E}_{x\backsim P}logQ(x)$ 针对Q最小化交叉熵等价于最小化KL散度

$lim_{x\to 0}xlogx=0$

结构化概率模型&图论

概率分布可以分解为多个概率乘积的形式 结构化概率模型/图模型：使用图来表示概率分布的分解

有向图模型：使用条件概率分布来表示概率分布的分解 父节点$Pa\mathcal{G}(x_{i})$：组成每个随机变量$x_{i}$条件概率的影响因子 $P(x)=\prod\limits_{i}p(x_{i}|Pa\mathcal{G}(x_{i}))$

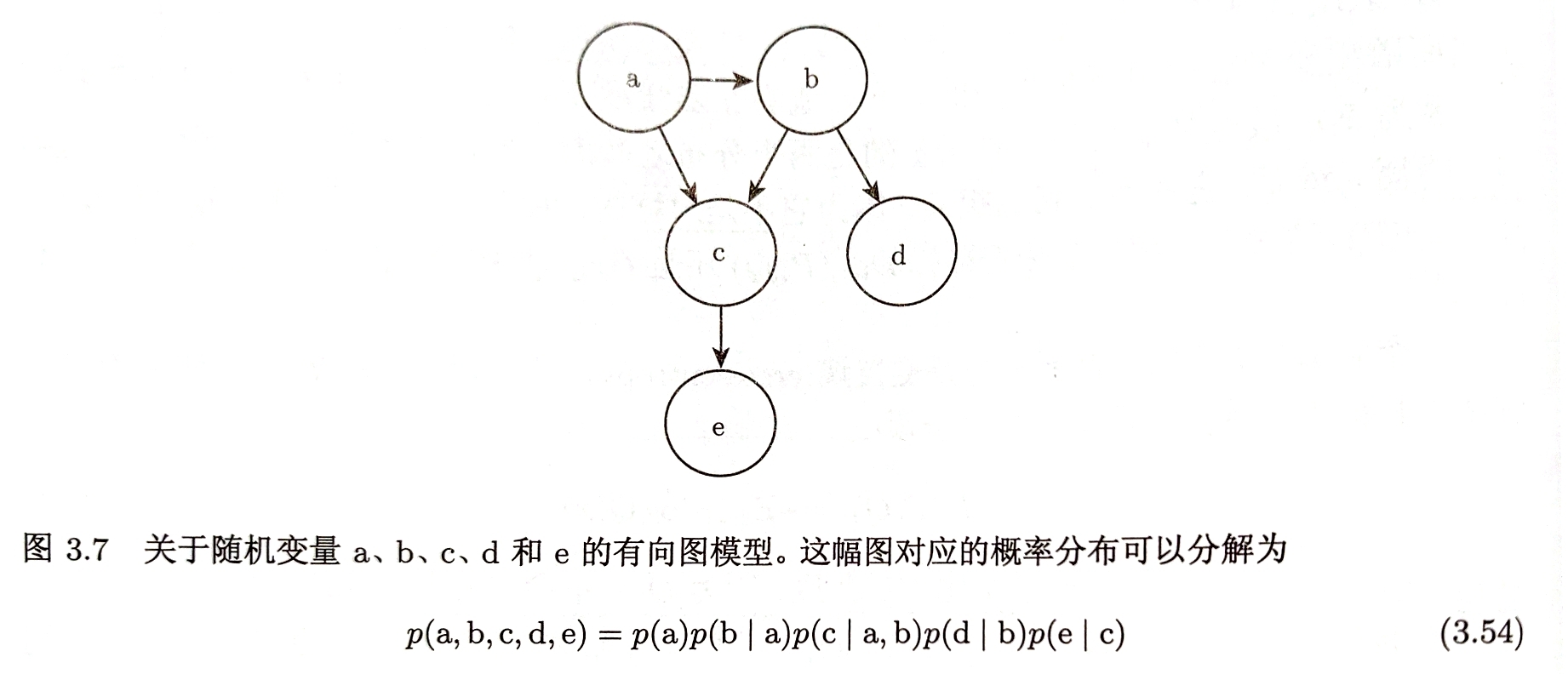
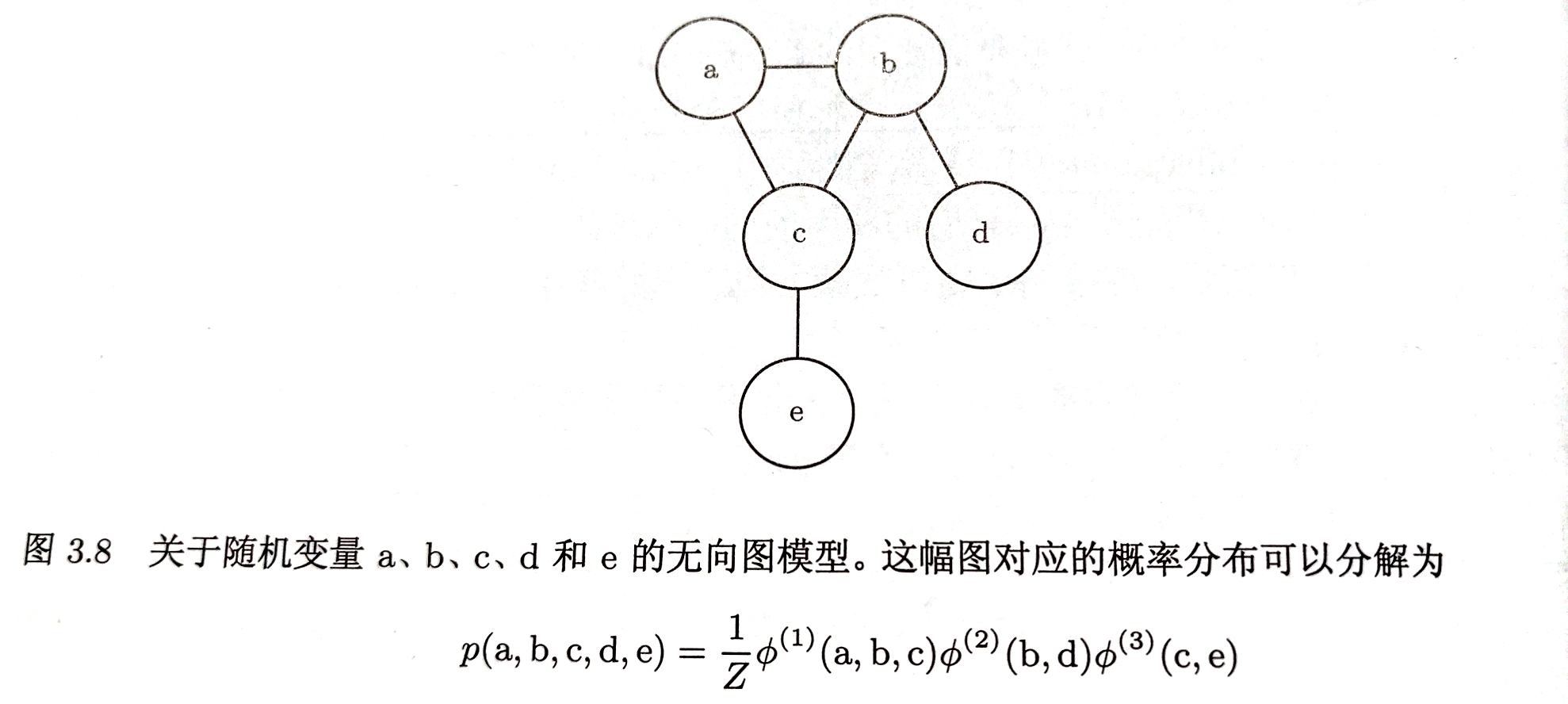
无向图模型：将概率分布分解为一组函数 函数不是任何类型的概率分布 团：$\mathcal{G}$中任何两两有边连接的顶点的集合 每个团$\mathcal{C}^{i}$都伴随一个因子$\phi^{i}(\mathcal{C}^i)$ 每个因子都是非负的，但不要求积分为1 随机变量的联合概率与所有因子的乘积成比例 归一化常数Z $p(x)= \frac{1}{Z}\prod\limits_{i}\phi^{i}(\mathcal{C}^{i})$

• Previous
  【Deep Learning】第2章 线性代数
• Next
  【Deep Learning】第4章 数值问题