第6章 前馈神经网络
深度前馈网络（deep feedforward network） 前馈神经网络（feedforward neural network） 多层感知机（multilayer perception，MLP）
前馈：信息流过$x$的函数，流经$f$的中间计算过程，最终达输出$y$ 前馈模型输出与模型本身之间没有就反馈连接 循环神经网络：前馈神经网络扩展成包含反馈连接
网络：通常用许多不同函数复合在一起表示 深度：函数的链式结构$f(x)=f^{3}(f^{2}(f^{1}(x)))$；$f^{1}$第一层$f^{2}$第二层；链的全长为模型的深度；前馈网络的最后一层为输出层 训练数据没有给出每一层所需的输出，所以这些层成为隐含层
将线性模型扩展到非线性：线性模型不作用于$x$，作用于变换后的输入$\phi(x))$上，$\phi$是非线性变换【激活函数】
深度学习的策略是学习$\phi$
线性扩展至非线性
线性模型不能解决异或（XOR）问题
将非线性特征映射在变换空间中，进而使线性模型可用
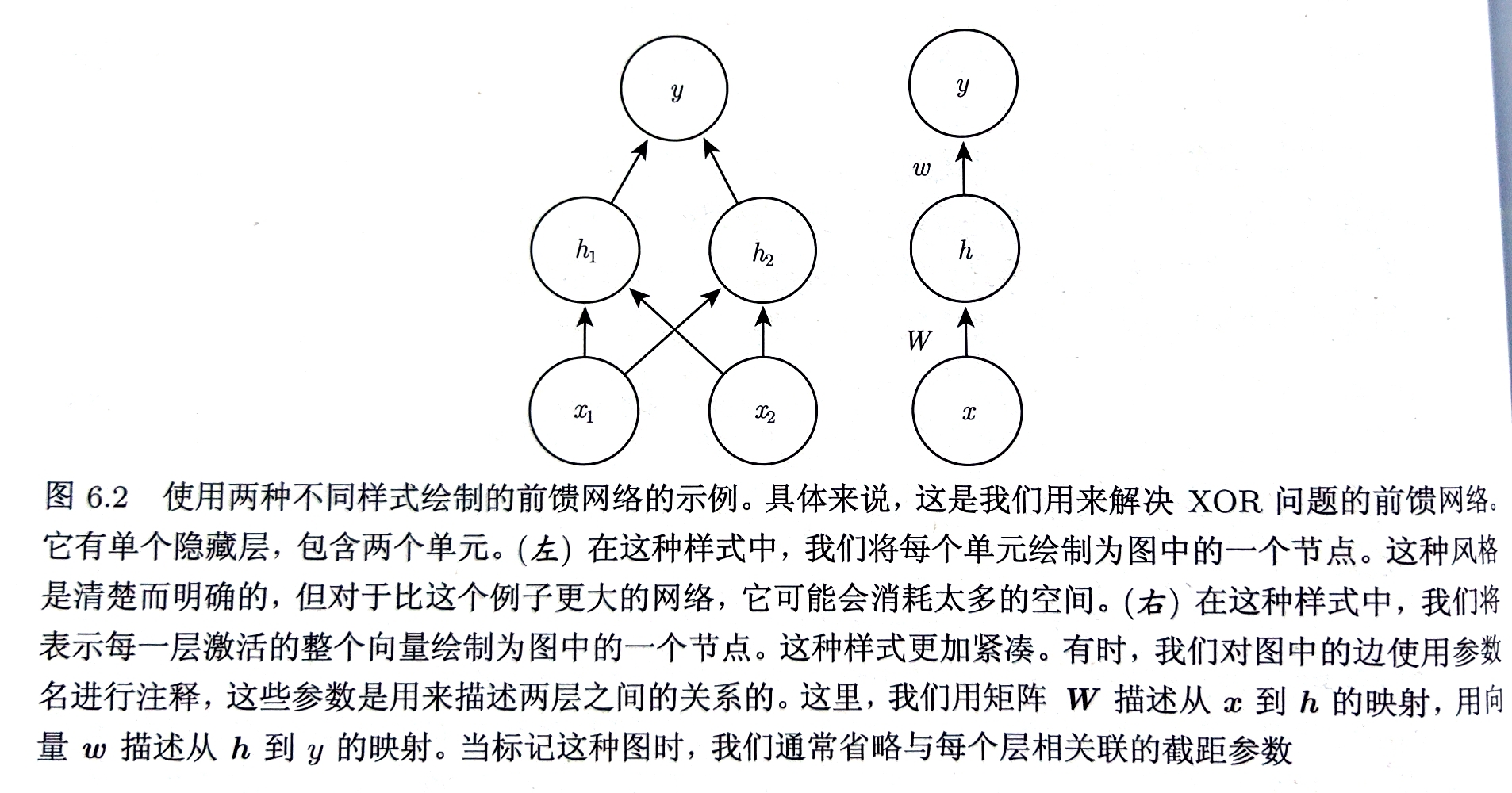模型$f(x;W,c,w,b)=f^{2}(f^{1}(x))$
若$f^{1}$是线性的，则整个模型仍是线性的
大多数神经网络通过仿射变换（线性变化+平移）后紧跟激活函数（固定非线性函数）实现非线性描述$h=g(W^{T}x+c)$
参数：$W$线性变换的权重矩阵；$c$偏置（极大提高了线性分割的灵活性)
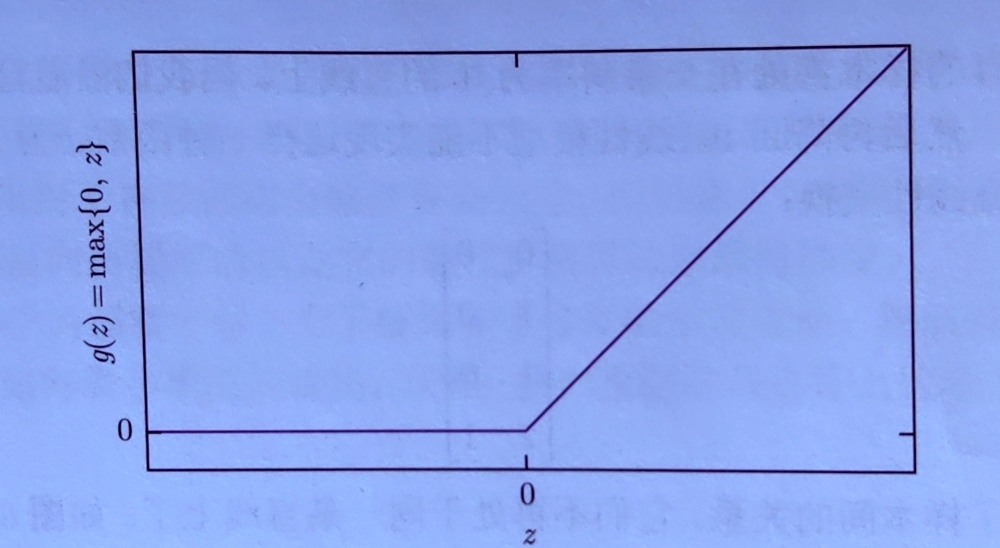
现代神经网络中，默认推荐的激活函数为ReLU（斜坡函数）$g(z)=max{0,z}$ ReLU优势：
- 简化计算过程，计算简洁迅速
- 更有效的梯度下降和反向传播，避免了梯度爆炸和梯度消失
- 函数负部为0造成网络稀疏性，减少了参数间依存关系，缓解过拟合
异或问题整个网络：$f(x;W,c,w,b)=w^{T}max{0,W^{T}x+c}+b$
基于梯度的学习
神经网络的非线性导致多数常用代价函数非凹——没有收敛性保证，对参数的初始值敏感 神经网络通常采用迭代的、基于梯度的优化，使代价函数达到一个小值 通常将所有的权重初始化为小随机数，偏置初始化为0或小正值
目标函数
多数现代的神经网络使用最大似然训练，则代价函数为负的对数似然，等价于训练数据和模型分布间的交叉熵 $J(\theta)=-\mathbb{E}{x,y\thicksim\hat{p}{data}}log\ p_{model}(y|x)$ 优势：
-
减轻了为每个模型设计代价函数的负担，明确模型则确定了代价函数$log\ p(y x)$ - 消除了某些输出单元的指数效果，防止绝对值极大的负值导致饱和（非常平缓）函数使梯度极小
- 交叉熵代价函数通常没有最小值
学习条件统计量 若使用一个足够强大的神经网络，可以认为这个神经网络能够代表一大类函数中的任意函数$f$，而不是具有特殊的参数形式 把代价函数看做泛函（functional，是函数到实数的映射） 变分法
输出单元
任何可用作输出的神经网络单元，也可以被用作隐藏单元
高斯输出分布：线性单元 基于仿射的输出单元 仿射变换仍为线性，这些单元为线性单元 给定特征$h$，线性输出单元层产生一个向量$\hat{y}=W^{T}h+b$
线性输出层经常被用于产生条件高斯分布的均值：$P(y|x)=\mathcal{N}(y;\hat{y},I)$最大化对数似然此时等价于最小化均方误差 最大似然框架使得更容易使高斯分布的协方差矩阵作为输入的函数；但协方差矩阵必须为正定矩阵 线性输出层很难满足正定协方差矩阵，需要其他输出单元对协方差参数化
线性输出单元不会饱和，易于采用基于梯度的优化算法
伯努利输出分布：Sigmoid单元 对于二值型变量，当模型给定的输出$w^{T}h+b$位于$[0,1]$之外时，线性单元$P(y=1|x)=max{0,min{1,w^{T}h+b}}$梯度为0
需要选择无论任何输出都有较大的梯度的输出单元 即：sigmoid输出单元结合最大似然$\hat{y}=\sigma(w^{T}h+b)$ 首先使用线性层计算$z=w^{T}h+b$，再使用sigmoid激活函数将$z$转化为概率
logit分对数变量$z$：基于指数和归一化的概率分布 $log \frac{P(y=1|x)}{1-P(y=1|x)}=w^{T}h+d$ 与最大似然学习契合：对数最大似然与$logit$指数抵消，去除了sigmoid函数饱和性阻止梯度改进的问题——变成了softplus函数的形式，当且仅当模型得到正确答案时函数饱和 其他损失函数（如均方误差）会在sigmoid函数饱和时饱和 最大似然几乎总是训练sigmoid输出单元的优选方法
多重伯努利输出分布：softmax单元 任何时候表示一个具有$n$个可能取值的离散型随机变量的分布时都可以使用softmax函数 Softmax函数常用于分类器的输出，表示多分类的概率分布；少用于模型内部 可视作sigmoid的扩展
- 线性层预测未归一化的对数概率$z=W^{T}h+b$ 其中$z_{i}=log\ \hat{P}(y=i|x)$
- 使用最大化对数似然训练$softmax(z){i}= \frac{e^{z{i}}}{\sum\limits_{j}e^{z_{j}}}$输出目标值$y$，即$log\ P(y=i;z)=log\ softmax(z){i}=z{i}-log\sum\limits_{j}e^{z_{j}}$ 第一项输入$z_{i}$不会饱和，最大化对数似然鼓励第一项被推高，第二项鼓励所有的$z$被压低，强烈地惩罚最活跃的不正确预测
不使用对数抵消Softmax中指数的目标函数，在指数函数变量取非常小负值时会造成梯度消失问题；平方误差目标函数对Softmax单元效果极差
当输入值之间的差异变得极端时，Softmax可能饱和 Softmax函数对所有输入同时增加一常数时输出不变 数值方法稳定的Softmax函数变体：$softmax(z)=softmax(z-\mathop{\max}\limits_{i}z_{i} )$
由于Softmax中$n$个输出总和必须为1，故固定$z$的一个元素，如$z_{n}=0$
高斯混合输出分布：混合密度网络 基于梯度的优化方法对混合条件高斯输出可能是不可靠的 解决方法：梯度截断；启发式缩放梯度 高斯混合输出在语音生成模型、物理运动中特别有效
隐藏单元
隐藏单元的选择是前馈神经网络独有的问题 ReLU单元是隐藏单元的默认选择
部分隐藏单元在部分输入点上不可微，梯度下降理论上无效，但表现仍然足够好。因为神经网络训练算法通常不会达到代价函数局部最小值
ReLU $h=g(w^{T}x+b)$ 通常作用于仿射变化 优点：易于优化 缺点：不能通过基于梯度的方法使为0的样本激活 初始值：$b$的所有元素设置为小的正值，如0.1
3个扩展：当$z_{i}<0$时使用非零的斜率 $a_{i}:h_{i}=g(z,\alpha){i}=max(0,z{i})+\alpha_{i}min(0,z_{i})$ 绝对值整流$\alpha_{i}=-1,g(z)=|z|$ 用于图像的对象识别，寻找在输入照明极性反转下不变的特征 渗漏整流线性单元$\alpha_{i}$固定为极小值，如0.01 PReLU$\alpha_{i}$为学习的参数
maxout单元
ReLU的进一步扩展
将$z$划分为每组具有$k$个值的组，输出每组中最大的元素
$g(z){i}=\mathop{\max}\limits{j\in\mathbb{G}^{i}}z_{j},\mathbb{G}^{i}为组i的输入索引集{(i-1)k+1,…,ik}$
maxout可以学习k段分段线性的凸函数
maxout单元可以视作激活函数本身，调整$k$，maxout单元可以以任意精度近似任何凸函数
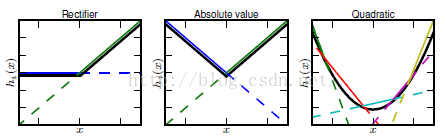优点：可以拟合任意凸函数；具有冗余对抗灾难以往
缺点：每个maxout单元需要$k$个权重向量来参数化，需要更多的正则化
logistics sigmoid激活函数与双曲正切函数 $g(z)=\sigma(z)$&$g(z)=tanh(z)$ 其中$tanh(z)=2\sigma(2z)-1$ sigmoid函数在大部分定义域中饱和，仅在接近0附近敏感 不鼓励作为前馈神经网络中的隐藏单元 需要合适的代价函数抵消sigmoid的饱和性
双曲正切激活函数通常比logistic sigmoid表现更好 $tanh(0)=0而\sigma(0)=0.5$
其他隐藏单元 很多可微函数表现都很好，在一些问题上能达到与传统隐藏单元差不多的水平，但没有重大突破不会被发布
特殊：
- 线性隐藏单元减少网络中参数数量 $n$个输入和$p$个输出的神经网络层$h=g(W^{T}x+b)$视作两层 对权重矩阵$W$因式分解为$U,V$ 第一层没有激活函数，权重矩阵为U；第二层权重矩阵$V$ $h=g(V^{T}U^{T}x+b)$，参数为$(n+p)q$个，原始参数$np$个 当$q$很小时，可以很大的节省参数（将线性变换约束为低秩）
- softmax作为隐藏单元用于明确学习操作内存的高级结构
- 径向基函数RBF
- softplus函数
- 硬双曲正切函数
架构设计
架构指神经网络的结构，包括单元数量及单元连接方式 大多数神经网络通过链式结构布置层，每一层为前一层的函数 架构设计主要考虑网络的深度和每一层的宽度 更深层的网络通常能对每一层减少使用的单元数和参数，且更易泛化，但难以优化
万能近似定理：一个前馈神经网络如果具有线性输出层和至少一层具有任何一种“挤压”性质的激活函数的隐藏层，只要给予网络足够数量的隐藏单元，它可以以任意精度近似任何从一个有限维空间到另一个有限维空间的Borel可测函数。前馈网络的导数也可以任意精度近似函数的导数。 定义在$\mathbb{R}^{n}$的有界闭集上的任意连续函数是Borel可测的。 即任意函数，有一个大的多层感知机MLP一定能够表示这个函数。但训练的优化算法未必找到期望函数的参数值；也可能因为过拟合选择了错误的函数。
更深的模型似乎在广泛的任务中泛化的更好 信念：学习的函数应该有多个简单函数复合而成
一般而言，层不需要连接在链中，尽管这是常见做法；许多架构构建了主链后又添加了额外的架构特性，如跳板
减少连接数量的策略减少了参数的数量以及计算量，但通常高度依赖于问题
反向传播算法backprop
反向传播算法仅指用于计算梯度的方法，原则上可以计算任何函数的导数 核心是链式法则
计算图
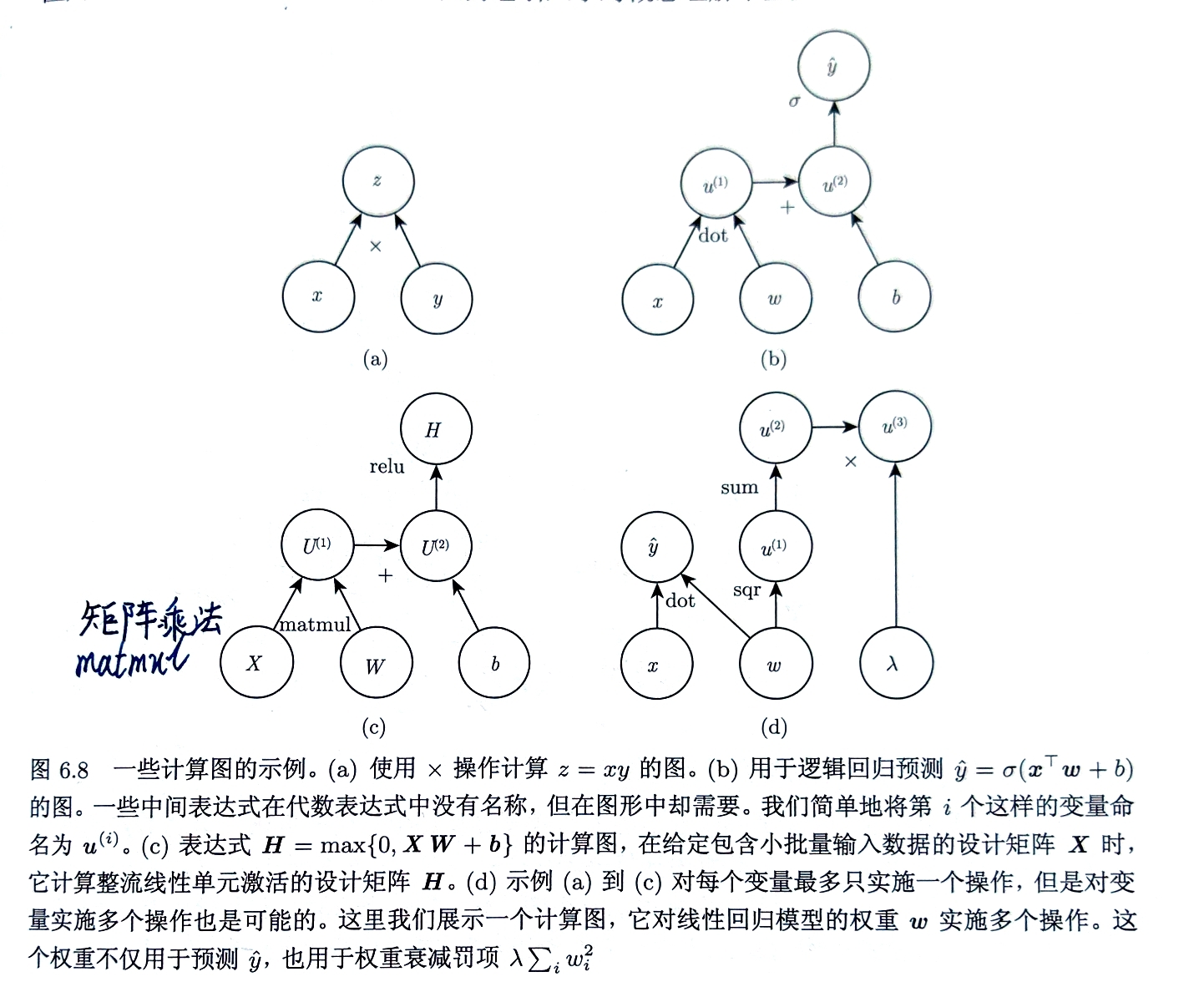链式法则$z=f(g(x))=f(y)$
$\frac{dz}{dx}=\frac{dz}{dy} \frac{dy}{dx}$
$\frac{\partial z}{\partial x_{i}}=\sum\limits_{j} \frac{\partial z}{\partial y_{i}} \frac{\partial y_{i}}{\partial x_{i}}$
向量$\bigtriangledown_{x}z=(\frac{\partial y}{\partial x})^{T}\bigtriangledown_{y}z$
张量$\bigtriangledown_{\mathbf{X}}z=\sum\limits_{j}(\bigtriangledown_{\mathbf{X}}\mathbf{Y}{j})\frac{\partial z}{\partial \mathbf{Y{j}}}$
单个标量反向传播
前向传播算法
$for\ i=1,…,n_i , do$ $\quad u_i ← x_i$ $end\ for$ $for\ i=n_i+1,…,n do$ $\quad\mathbb{A}^{i} ←{u^{j}|j\in Pa(u^{i}}$ $\quad u^{i}←f^{i}(\mathbb{A}^{i})$ $end\ for$ $return\ u^{n}$
反向传播算法（全标量）
通过链式法则将输出层获取的代价函数偏导向输入层方向传递
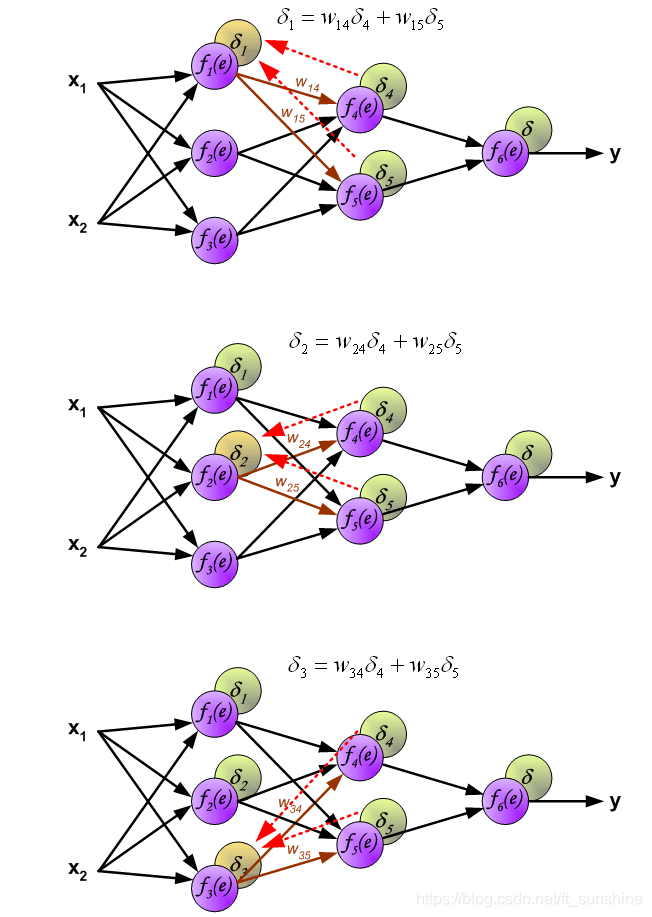
$运行前向传播算法获取网络的激活$ $初始化grad_{table}用于存储计算好的导数数据结构$ $grad_{table}[u^{i}]存储 \frac{\partial u^{n}}{\partial u^{i}}的值$ $grad_{table}[u^{n}]←1$ $for\ j=n-1\ down\ to\ 1\ do$ $\quad下一行使用存储的值计算 \frac{\partial u^{n}}{\partial u^{j}}=\sum\limits_{i:j\in Pa(u^{i})} \frac{\partial u^{n}}{\partial u^{i}} \frac{\partial u^{i}}{\partial u^{j}}$ $\quad grad_{table}[u^{j}]←\sum\limits_{i:j\in Pa(u^{i})} grad_{table}[u^{i}] \frac{\partial u^{i}}{\partial u^{j}}$ $end\ for$ $return\ {grad_{table}[u^{i}]|i=1,…,n_{i}}$
反向传播算法为减少公共子表达式数量而不考虑存储的开销
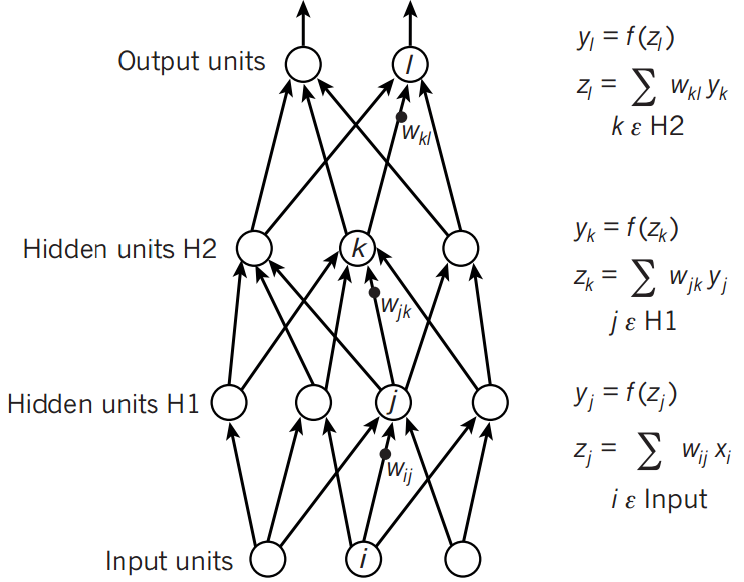
全连接MLP中的反向传播算法
总代价$J$；正则项$\Omega(\theta)$，$\theta$包含所有参数（权重&偏置） 仅考虑单个输入样本$x$ $Require：网络深度$ $Require：W^{i},i\in{1,…,l}，模型的权重矩阵$ $Require：b^{i},i\in{1,…,l}，模型的偏置矩阵$ $Require：x，程序的输入$ $Require：y，目标输出$ $h^{0}=x$ $for\ k=1,…,l do$ $\quad a^{k}=W^{k}h^(k-1)+b^{k}$ $\quad h^{k}=f(a^{k})$ $end\ for$ $\hat{y}=h^{l}$ $J=L(\hat{y},y)+\lambda\Omega(\theta)$ $前向传播完成，计算顶层梯度，开始反向传播$ $g ← \bigtriangledown_{\hat{y}}J=\bigtriangledown_{\hat{y}}L(\hat{y},y)$ $for\ k=l,l-1,…,1\ do$ $\quad 将关于层输出的梯度转化为非线性激活输入前的梯度$ $\quad g ← \bigtriangledown_{a^{k}}J=g\odot f’(a^{k})$ $\quad 计算权重、偏置的梯度（若需还有正则项）$ $\quad \bigtriangledown_{b^k}J=g+\lambda\bigtriangledown_{b^{k}}\Omega(\theta)$ $\quad \bigtriangledown_{W^{K}}J=g{h^{k-1}}^{\top}+\lambda\bigtriangledown_{W^{k}}\Omega(\theta)$ $\quad 更低一层的隐藏层传播梯度$ $\quad g ← \bigtriangledown_{h^{k-1}}J={W^{k}}^{\top}g$ $end\ for$
|  |
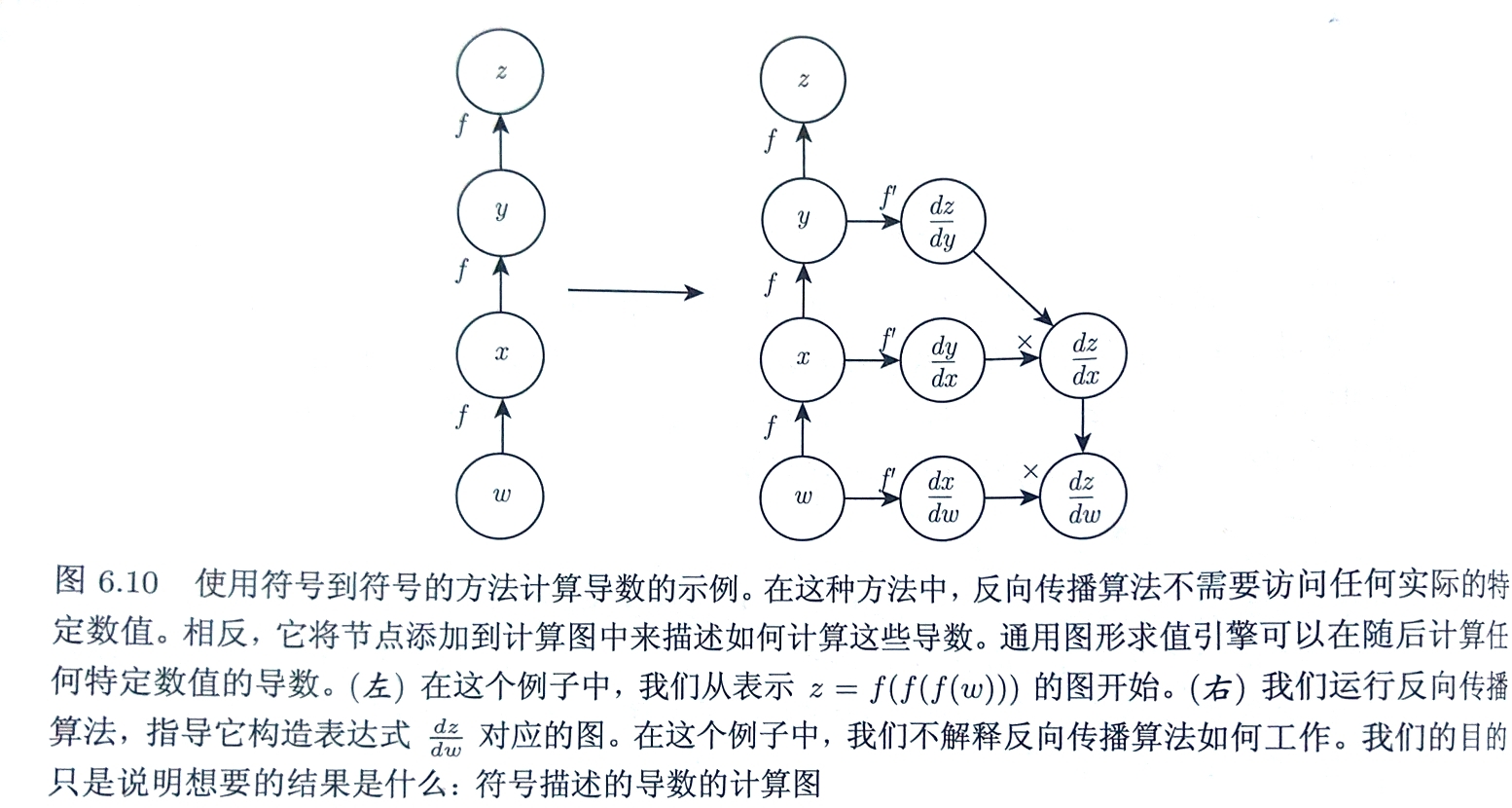一般化的反向传播
图$\mathcal{G}$ 中的每个节点对应着一个变量，为最大地一般化，将该变量描述为张量$\mathbf{V}$
子程序： get_operation($\mathbf{V}$)：返回用于计算$\mathbf{V}$的操作，代表了在计算图中流入$\mathbf{V}$的边【如矩阵乘法】 get_consumer($\mathbf{V},\mathcal{G}$)：返回一组变量，计算图$\mathcal{G}$中$\mathbf{V}$的子节点 get_inputs($\mathbf{V},\mathcal{G}$)：返回一组变量，计算图$\mathcal{G}$中$\mathbf{V}$的父节点
每个操作op与bprop操作相关联 bprop操作计算Jacobian向量机 op.bprop(inputs,$\mathbf{X},\mathbf{G}$)返回$\sum\limits_{i}(\bigtriangledown_{x}op.f(inputs){i})G{i}$ $G$为操作对于输出的梯度
反向传播算法外围骨架 进行简单设置和清理工作 $\begin{aligned} Re&quire:\mathbb{T},需要计算梯度的目标变量集 \ Re&quire:\mathcal{G},计算图\ Re&quire:z,要微分的变量\ &令\mathcal{G’}为\mathcal{G}剪枝后的计算图，仅包括z的祖先以及\mathbb{T}中节点的后代\ &初始化grad_table作为关联张量和对应导数的数据结构\&grad_table[z]\leftarrow 1\ &for\ \mathbf{V}\in\ \mathbb{T}\ do\& \quad build_grad(\mathbf{V},\mathcal{G},\mathcal{G’},grad_{tabel)}\&end\ for\&Return grad_{table}\ restricted\ to\ \mathbb{T}\end{aligned}$
反向传播算法的内循环子程序$build_grad(\mathbf{V},\mathcal{G},\mathcal{G’},grad_table)$ $\begin{aligned}Re&quire:\mathbf{V},应被加到\mathcal{G}和grad_table的变量\Re&quire:\mathcal{G}\Re&quire:\mathcal{G’},根据参与梯度的节点\mathcal{G}的受限图\Re&quire:grad_table,将节点映射到对应梯度的数据结构\&if\ \mathbf{V}\ is\ in\ grad_table\ then\&\quad Return\ grad_table[\mathbf{V}]\&end\ if\&i\leftarrow1\&for\ \mathbf{C}\ in\ get_consumers(\mathbf{V},\mathcal{G’})\ do\ &\quad op\leftarrow get_operation(\mathbf{C})\ &\quad D\leftarrow buld_grad(\mathbf{C},\mathcal{G},\mathcal{G’},grad_table)\&\quad\mathbf{G^{i}}\leftarrow op.bprop(get_inputs(\mathbf{C},\mathcal{G’},\mathbf{V},\mathbf{D}\&\quad i\leftarrow i+1\&end\ for\ &\mathbf{G}\leftarrow \sum\limits_{i}\mathbf{G^{i}}\&grad_table[\mathbf{V}]=\mathbf{G}\&Return\ \mathbf{G}\end{aligned}$
反向传播算法是自动微分的一种方法，是反向模式累加（reverse mode accumulation)的特例
其他自动微分：如前向模式累加（擅长处理图的输出数目大于输入数目），用于循环神经网络梯度的实时计算