第7章 深度学习中的正则化
参数范数惩罚
正则化后的目标函数$\tilde{J}(\theta;X,y)=J(\theta;X,y)+\alpha\Omega(\theta)$ 其中$\alpha\in [0,\infty)$是权衡范数惩罚项$\Omega$和标准目标函数$J$相对贡献的超参数
最小化正则化后的目标函数$\tilde{J}$会降低标准目标$J$关于测试集的误差并减小在某些衡量标准下参数子集$\theta$的规模
神经网络中，参数包括每一层仿射变换的权重和偏置，通常只对权重做正则惩罚，不对偏置做正则惩罚 每个偏置仅控制一个单变量，不会导致太大的方差，且正则化偏置可能导致明显的欠拟合
寻找多个合适的超参数代价很大，为减少搜索空间，通常在所有层使用相同的权重衰减
$L^2$ 参数正则化 权重衰减 $\Omega(\theta)= \frac{1}{2}||w||_{2}^{2}$
目标函数$\tilde{y}(w;X,y)= \frac{\alpha}{2}w^{T}w+J(w;X,y)$ 梯度$\bigtriangledown_{w}\tilde{y}(w;X,y)=\alpha w+\bigtriangledown_{w}J(w;X,y)$ 权重更新$w\leftarrow w-\eta(\alpha w+\bigtriangledown_{w}J(w;X,y))$ $\Rightarrow\ w\leftarrow(1-\eta \alpha)w-\eta\bigtriangledown_{w}J(w;X,y)$ 加入权重衰减正则化后，每步执行梯度更新之前先收缩权重向量
权重衰减的效果是沿着由标准目标函数$J$在其最小化时的权重向量$w^{}$处计算的Hessian矩阵的特征向量所定义的轴缩放$w^{}$
根据$\frac{\lambda_{i}}{\lambda_{i}+\alpha}$因子缩放与$H$第$i$个特征向量对其的$w^{*}$的分量
沿着$H$特征值较大的方向正则化影响较小；特征值较小的方向会急剧收缩
即只有显著减小目标函数方向上的参数会保留相对完好；无助于目标函数减小的方向上的分量会因正则化而衰减掉
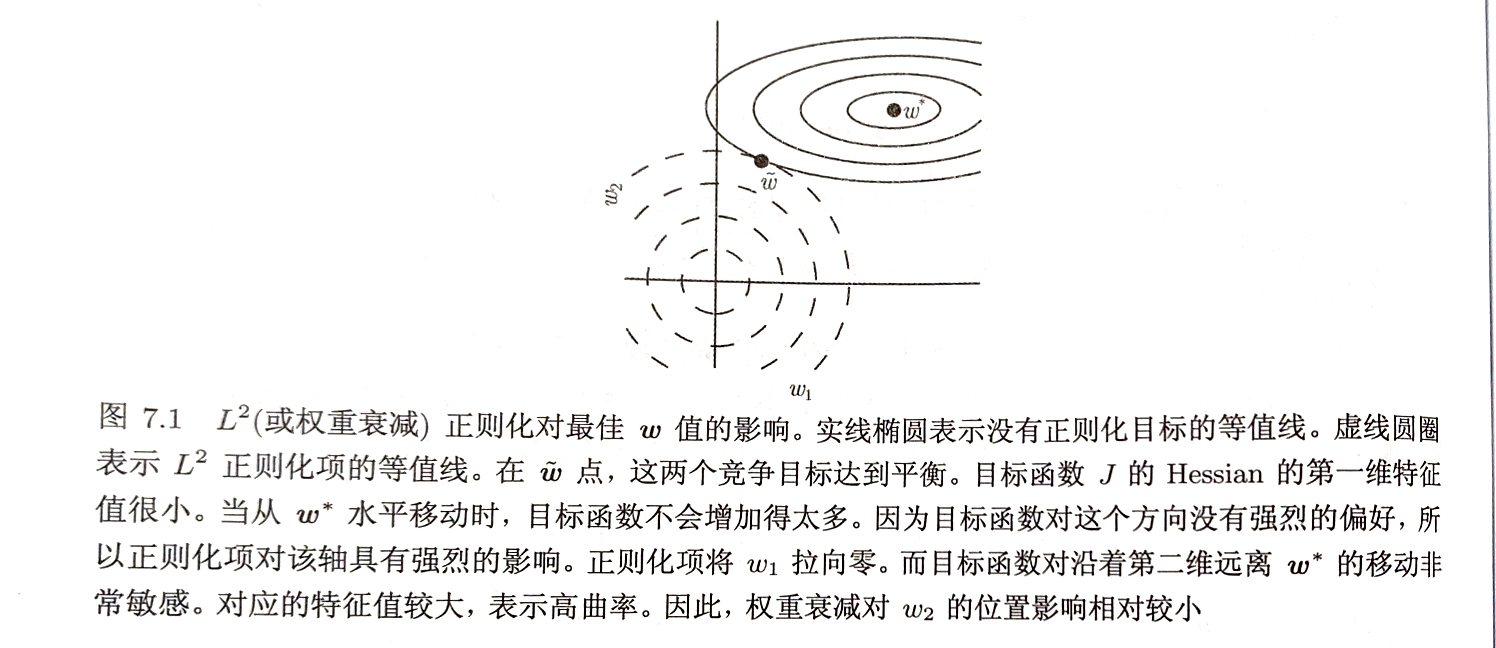
把参数范数惩罚看做对权重强加的约束，则权重被约束在一个$L^{2}$范数球中，$\alpha$越大约束区域越小
$L^{1}$正则化 $\Omega(\theta)=||w||{1}=\sum\limits{i}|w_{i}|$
正则化目标函数$\tilde{J}(w;X,y)=\alpha||w||{1}+J(w;X,y)$ 梯度$\bigtriangledown{w}\tilde{J}(w;X,y)=\alpha\ sign(w)+\bigtriangledown_{w}J(w;X,y)$
$L^{1}$正则化会产生稀疏解，令对最小化目标函数贡献较小的分量归零 $L^{1}$正则化被广泛用于特工选择
把参数范数惩罚看做对权重强加的约束，则权重被约束在一个$L^{1}$范数限制的区域内；$\alpha$越大约束区域越小
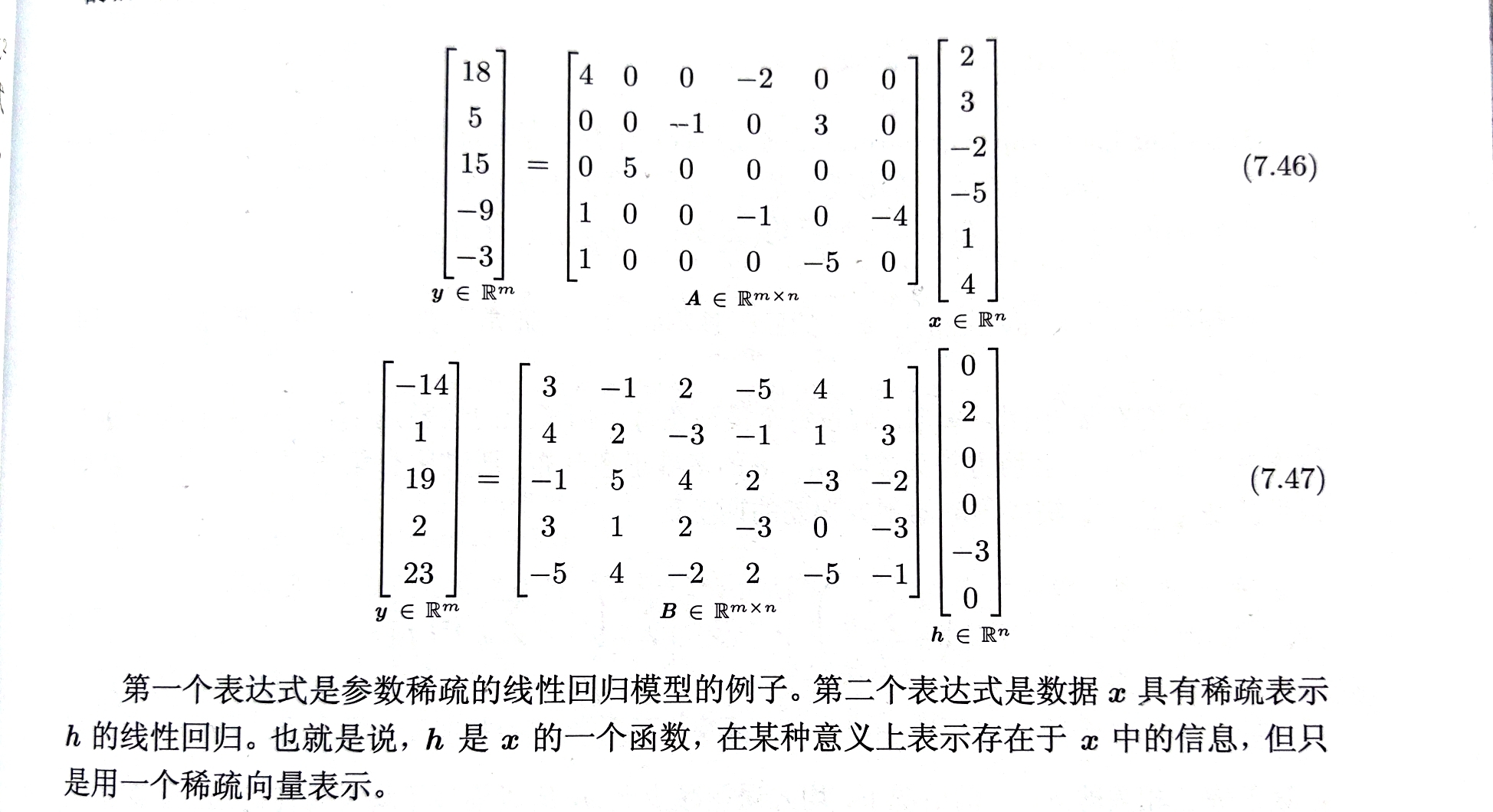
正则化有助于解决矩阵欠定的问题，保证了正则化矩阵是可逆的
数据集增强
当拥有的数据是有限的，可以通过创建假数据添加至训练集
数据集增强对图像识别特别有效 即使模型已经使用卷积和池化对部分平移保持不变，沿训练集图像每个方向平移几个像素的操作通常可以大大改善泛化；旋转或缩放也被证明非常有效【改变类别的旋转除外】
语音识别任务在神经网络输入层注入噪声也有效
向输入添加方差极小的噪声等价于对权重施加范数惩罚——Dropout算法 将噪声加到权重——循环神经网络
随机扰动的噪声推动模型进入到权重小的变化相对不敏感区域
大多数数据集的标签$y$都有一定错误，可以显式地对标签上的噪声建模。假设小常数$\epsilon$，训练集标记$y$正确的概率是$1-\epsilon$ 标签平滑：把确切分类目标从0,1替换为$\frac{\epsilon}{k-1}$和$1-\epsilon$，正则化具有$k$个输出的softmax函数的模型
半监督学习
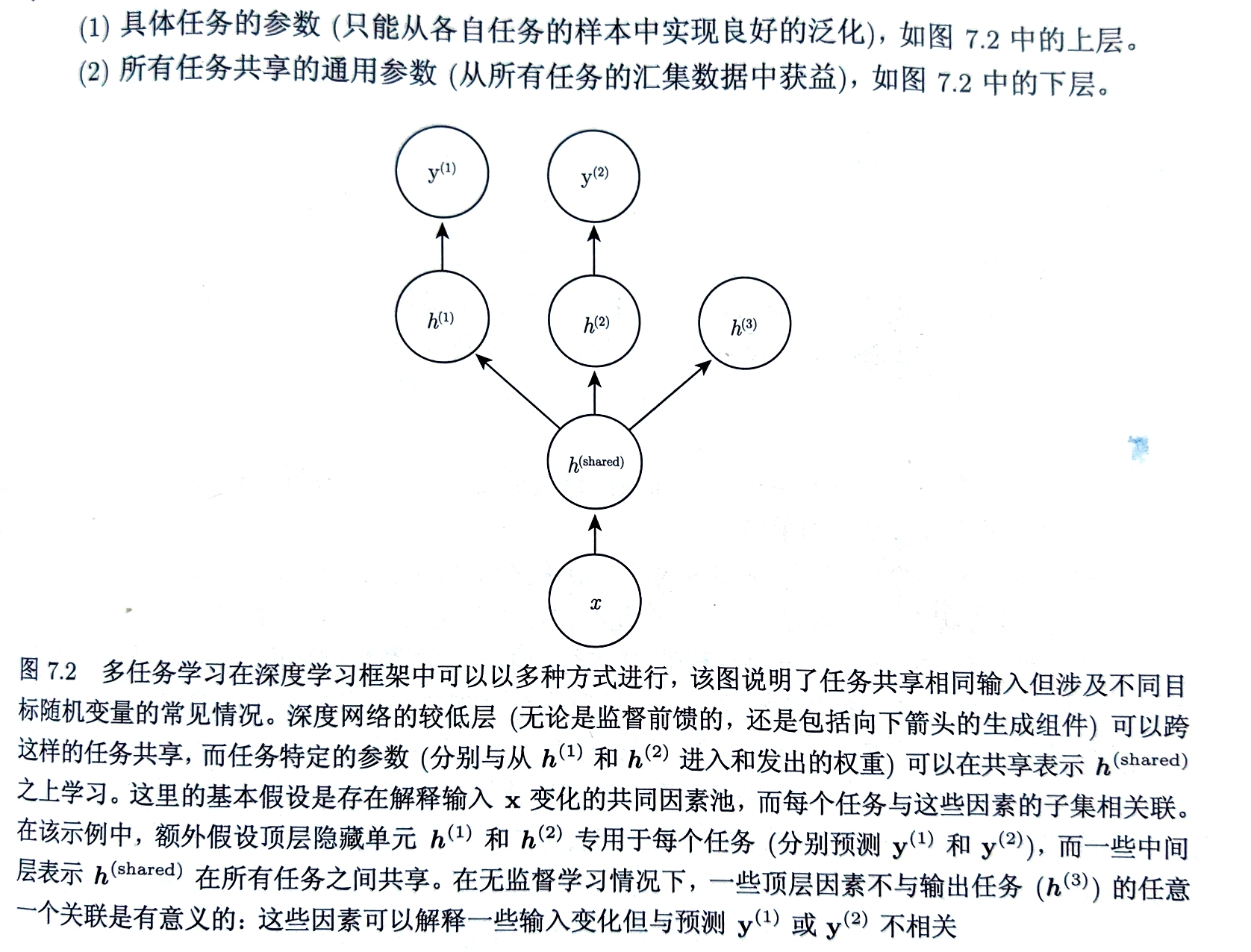
多任务学习 通过合并多个任务中的样例来提高泛化的一种方式 当模型的一部分被多个额外的任务共享时，这部分将被约束为良好的值，通常会带来更好的泛化能力 【共享要求任务之间存在某些统计关系的假设合理】
|  |
提前终止
深度学习中最常用的正则化 提前终止是非常高效的超参数选择算法 优点：
- 无需破坏学习动态的正则化
- 可以单独使用或与其他正则化结合 缺点：
- 训练期间需要定期评估验证集
- 需要保持最佳参数的副本
- 需要验证集，部分训练数据不能被馈送到模型
确定最佳训练步数的提前终止元算法 $\begin{aligned}&令n为评估间隔步数\&令p为耐心，即观察到较坏的验证集表现p次后终止\&令\theta_{o}为初始参数\&\theta\leftarrow \theta_{o}\&i\leftarrow 0\&j\leftarrow 0\&v\leftarrow\infty\&\theta^{}\leftarrow\theta\&i^{}\leftarrow i\&while\ j<p\ do\&\quad运行训练算法n步，更新\theta\&\quad i\leftarrow i+n\&\quad v^{‘}\leftarrow ValidationSetError(\theta)\&\quad if\ v^{‘}<v\ then\&\qquad j\leftarrow 0 \& \qquad \theta^{}\leftarrow \theta\&\qquad i^{}\leftarrow i\&\qquad v\leftarrow v^{‘}\&\quad else\&\qquad j\leftarrow j+1\&\quad end\ if\&end\ while\&最佳参数为\theta^{}，最佳训练步数为i^{}\end{aligned}$
降低验证集致使部分数据不能被馈送至模型的问题的两种方法 再次初始化模型，使用全部数据训练 $\begin{aligned}&令X^{train}和y^{train}为训练集\&将X^{train}和y^{train}分割为(X^{subtrain},X^{valid})和（y^{subtrain},y^{valid})\&从随机\theta开始使用X^{subtrain}作为训练集,X^{valid}和y^{valid}作为验证集\&运行提前终止元算法，返回最佳训练步数i^{}\&将\theta再次初始化为随机值\&在X^{train}和y^{train}上训练i^{}步\end{aligned}$
保持训练参数，使用全部数据继续训练 $\begin{aligned}&令X^{train}和y^{train}为训练集\&将X^{train}和y^{train}分割为(X^{subtrain},X^{valid})和（y^{subtrain},y^{valid})\&从随机\theta开始使用X^{subtrain}作为训练集,X^{valid}和y^{valid}作为验证集\&运行提前终止元算法，返回更新的\theta\&\epsilon\leftarrow J(\theta,X^{subtrain},y^{subtrain})\&while\ J(\theta,X^{valid},y^{valid})>\epsilon do\&\quad 在X^{train}和y^{train}上训练n步\&end\ while\end{aligned}$
提前终止将优化过程的参数空间约束在初始参数值$\theta_{0}$的小邻域内 与$L^{2}$正则化近似，至少在目标函数二次近似下等价 比$L^{2}$权重衰减更具优势，能自动确定正则化的正确量，无需进行多个超参数的训练实验
参数共享
根据先验知识获悉模型参数之间应该存在某些相关性 常见依赖：某些参数应当彼此接近
- 参数范数惩罚 有两个模型执行相同的分类任务（具相同类别），但输入分布稍微不同 形式地，有参数为$w^{A}$的模型A和$w^{B}$的模型B 两个模型将输入映射到两个不同但相关的输出$\hat{y}^{A}=f(w^{A},x)$和$\hat{y}^{B}=f(w^{B},x)$ 两个模型的参数应该彼此接近，即$\forall i,w_{i}^{A}$与$w_{i}^{B}$接近
| 可以通过正则化实现，如$L^{2}$参数范数惩罚$\Omega(w^{A},w^{B})= | w^{A}-w^{B} | _{2}^{2}$ |
Lasserre,2006提出正则化一个监督模型的参数，其实接近另一个无监督模式下训练的模型的参数
- 参数共享 使用约束的参数共享方法更为流行 强迫某些参数相等 优势：只有参数的子集需要被存储在内存中，可显著减少所占内存 典型算法：卷积神经网络CNN
稀疏表示
惩罚神经网络中的激活单元，稀疏化激活单元
参数稀疏&稀疏表示
表示的范数惩罚正则化：$\tilde{J}(\theta;X,y)=J(\theta;X,y)+\alpha\Omega(h)$
$L^{1}$惩罚诱导稀疏的表示：$\Omega(h)=||h||{1}=\sum\limits{i}|h_{i}|$
其他惩罚正则化：Student-t先验导出的惩罚；KL散度惩罚
- 通过激活值的硬约束获取稀疏表示 正交匹配追踪OMP-k方法 通过解决约束问题将输入值$x$编码成表示$h$ $\mathop{\arg\min}\limits_{h,||h||{0}<k}||x-Wh||^{2}$ 其中$||h||{0}$是$h$中非零项的个数 当$W$被约束为正交时，可以高效解决
OMP-1可以成为深度架构中非常有效的特征提取器
Bagging&Dropout
神经网络中随机初始化的差异、小批量的随机选择、超参数的差异或不同输出的非确定性实现往往足以使集成中的不同模型具有部分独立的误差 神经网络能够从模型平均中受益
Dropout可以被认为是集成大量深层神经网络的实用Bagging方法
Dropout训练的继承包括所有从基础网络除去非输出单元后形成的子网络
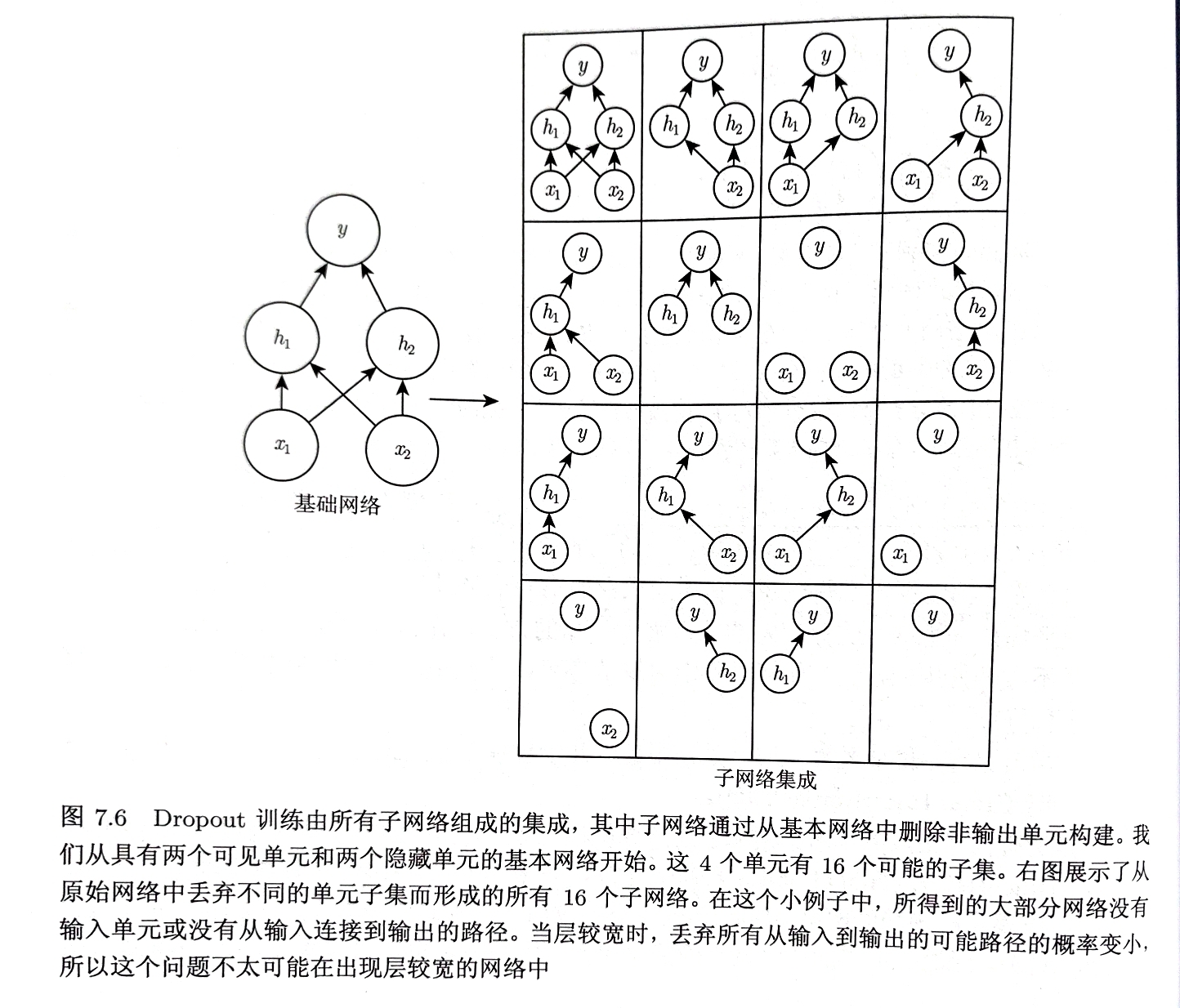神经网络仅需将一些单元的输出乘0就能有效删除一个单元
使用Dropout通常采用基于小批量产生较小步长的学习算法，如随机梯度下降
- 每次在小批量中加载一个样本，随机抽取应用于网络中所有输入和隐藏单元的不同二值掩码
- 每个单元掩码独立采样，掩码为1（包含单元）的采样概率为超参数
- 通常输入单元被包括的采样功率为0.8，隐藏单元被包含的概率为0.5
- 运行前向传播、反向传播及学习更新
Dropout中所有模型共享参数，每个模型继承父神经网络参数的不同子集 参数共享使在有限内存下表示指数级数量的模型可行
Dropout通常大部分模型没有显示地被训练，因为父神经网络通常很大，在每个步骤中我们只训练一小部分子网络，参数共享使剩余的子网络有好的参数设定
集成的预测 算术平均值$\sum\limits_{\mu}p(\mu)p(y|x,\mu)$ $p(\mu)是训练时采样\mu的概率分布$ 求和包含指数级的项，无法计算；通过平均许多掩码的输出推断
采用几何平均近似效果更佳 $\tilde{P}{ensemble}(y|x)=\sqrt[2^{d}]{\mathop{\prod}\limits{\mu}P(y|x,\mu)}$ $d为可被丢去的单元数$
Dropout几乎在所有使用分布式表示且可用随机梯度下降训练的模型上都表现良好
Dropout是正则化技术，减少了模型的有效容量，为抵消这种影响，必须增大模型规模 对于非常大的数据集，正则化带来的泛化误差减小的很少，此时使用Dropout和更大模型的计算代价可能超过正则化带来的好处 只有极少的训练样本，Dropout不会很有效
Dropout启发的其他随机方法训练指数级的共享权重的集成：DropConnect、随机池化
对抗样本
对输入样本故意添加一些人无法察觉的细微的干扰，导致模型以高置信度给出一个错误的输出
|  |
可以通过对抗训练减少原有独立同分布的测试集的错误
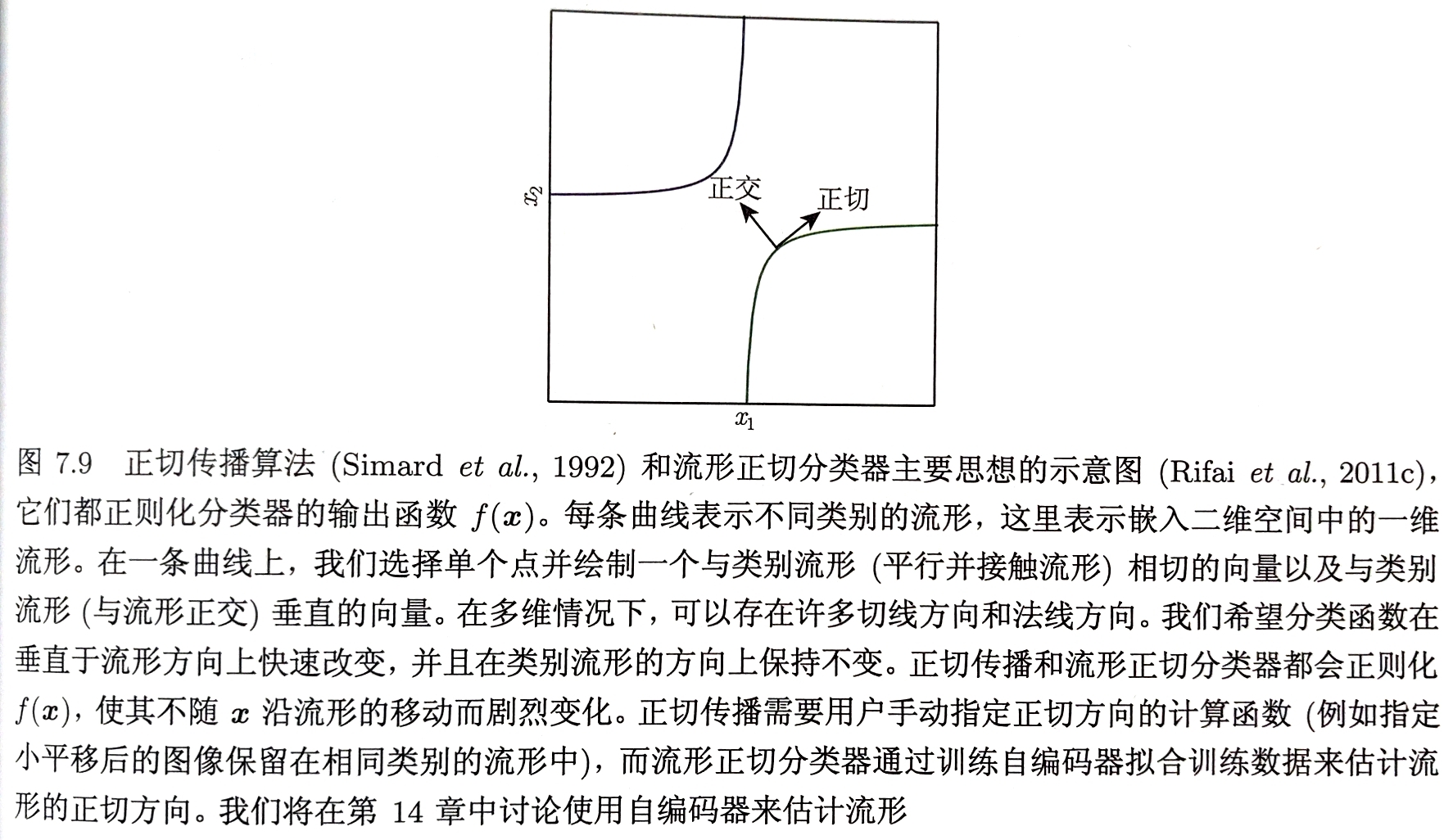
流形正切分类器
切面距离算法 假设尝试分类的样本和同一流形上的样本具有相同的类别 距离的度量不应使用欧氏距离，合理的距离是将点$x_{1}$和$x_{2}$各自所在的流形$M_{1}$和$M_{2}$的距离作为两点间的最近邻距离 由于计算困难，合理的替代是使用$x_{i}$处切平面近似$M_{i}$，并测量两条切平面或一个切平面和点之间的距离
正切传播算法
训练带有额外惩罚的神经网络分类器
目的使神经网络的每个输出$f(x)$对已知的变化因素（沿着相同样本聚集的流形的移动）是局部不变的
即：要求$\bigtriangledown_{x}f(x)$与已知流形（手动指定）的切向$v^{i}$正交，或等价地通过正则化惩罚$\Omega$使$f$在$x$的$v^{i}$方向的导数较小
$\Omega(f)=\sum\limits_{i}(\bigtriangledown_{x}f(x)^{\top}v^{i})^{2}$
