第9章 卷积网络
卷积神经网络CNN是一种专门用来处理具有类似网格结构的数据的神经网络 常用于时间序列数据(时间轴上的一维网格)和图像数据
卷积是一种线性运算 卷积网络指至少在网络的一层中使用卷积运算来代替一般的矩阵乘法运算的神经网络
卷积运算
通常用$\ast$表示卷积运算
$(x\ast w)(t)$一种加权平均的平滑估计
$x$为输入;$w$为核函数;输出有时被称作特征映射

连续形式卷积:$s(t)=(x\ast w)(t)=\int x(a)w(t-a)da$ 离散形式卷积:$s(t)=(x\ast w)(t)=\sum\limits_{\alpha=-\infty}^{\infty}x(a)w(t-a)$
二维卷积:$S(i,j)=(I\ast K)(i,j)=\sum\limits_{m}\sum\limits_{n}I(m,n)K(i-m,j-n)$ 卷积可交换:$S(i,j)=(I\ast K)(i,j)=(K\ast I)(i,j)$ 原因是核相对输入进行了翻转
神经网络中的卷积通常是互相关函数
互相关函数没有对核翻转,不可交换
机器学习中,卷积与其他函数一同使用,无论核是否翻转均不可交换
互相关函数:$S(i,j)=(I\ast K)(i,j)=\sum\limits_{m}\sum\limits_{n}I(i+m,i+n)K(m,n)$
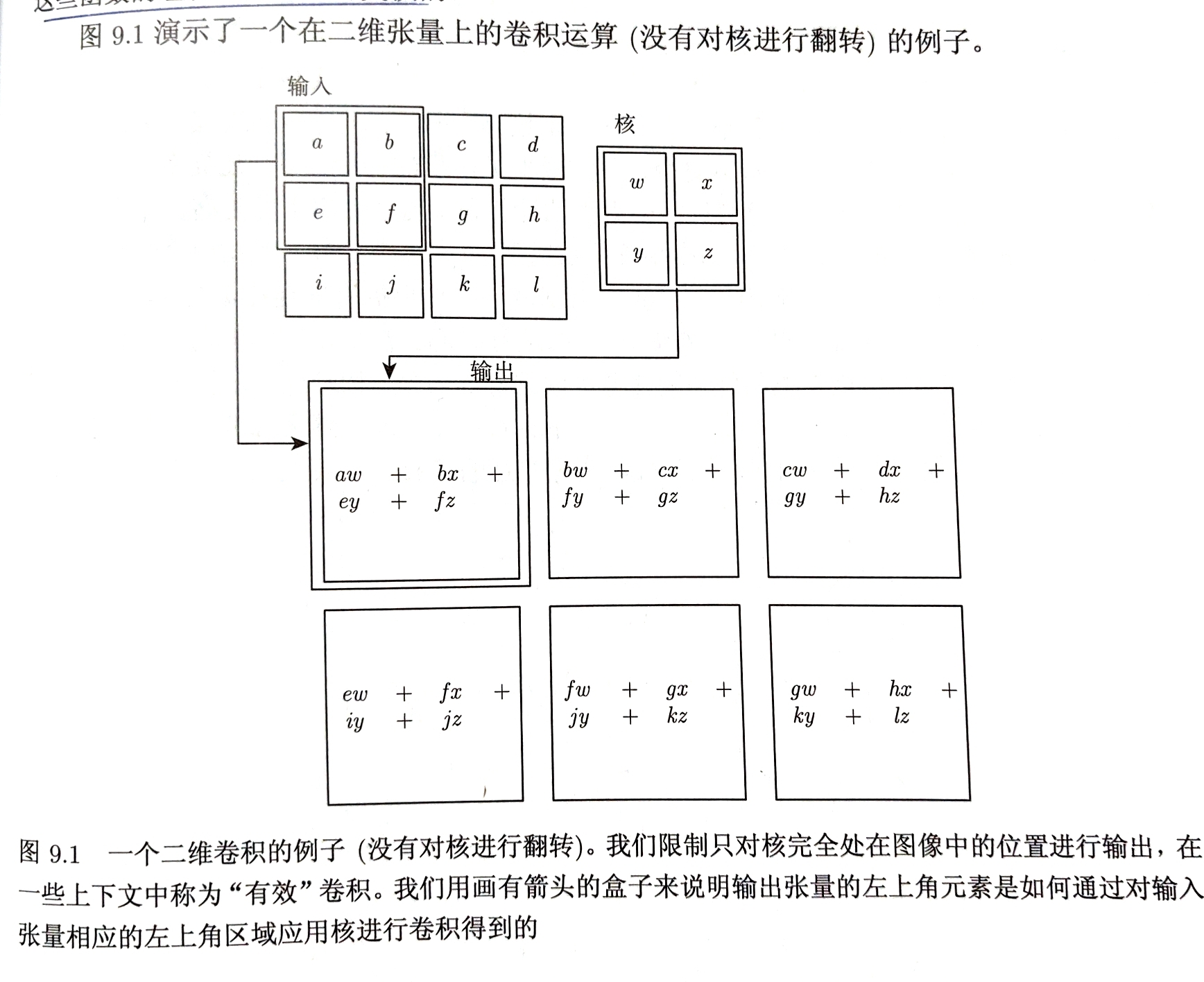
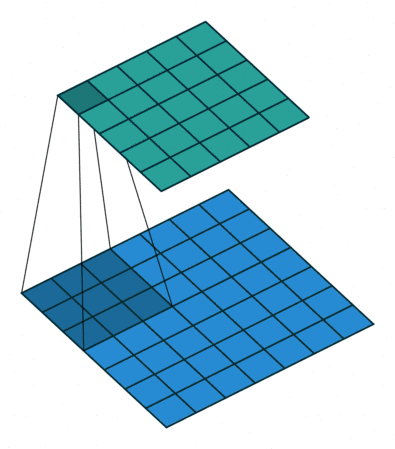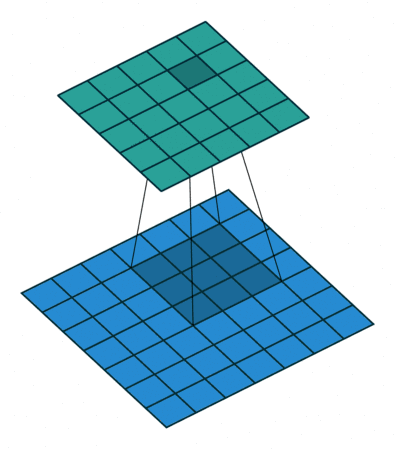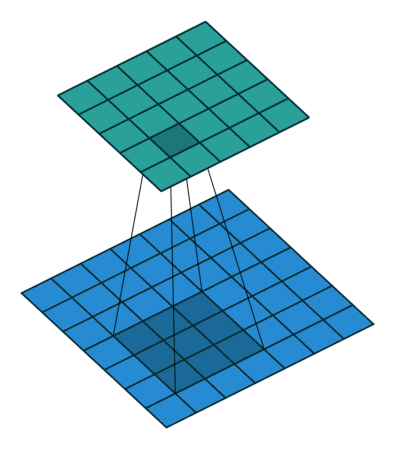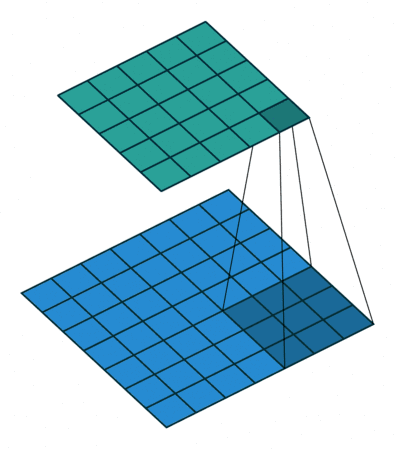
卷积运算通过稀疏交互、参数共享、等变表示改进机器学习 卷积提供了一种处理大小可变的输入的方法
稀疏交互
稀疏连接/系数权重
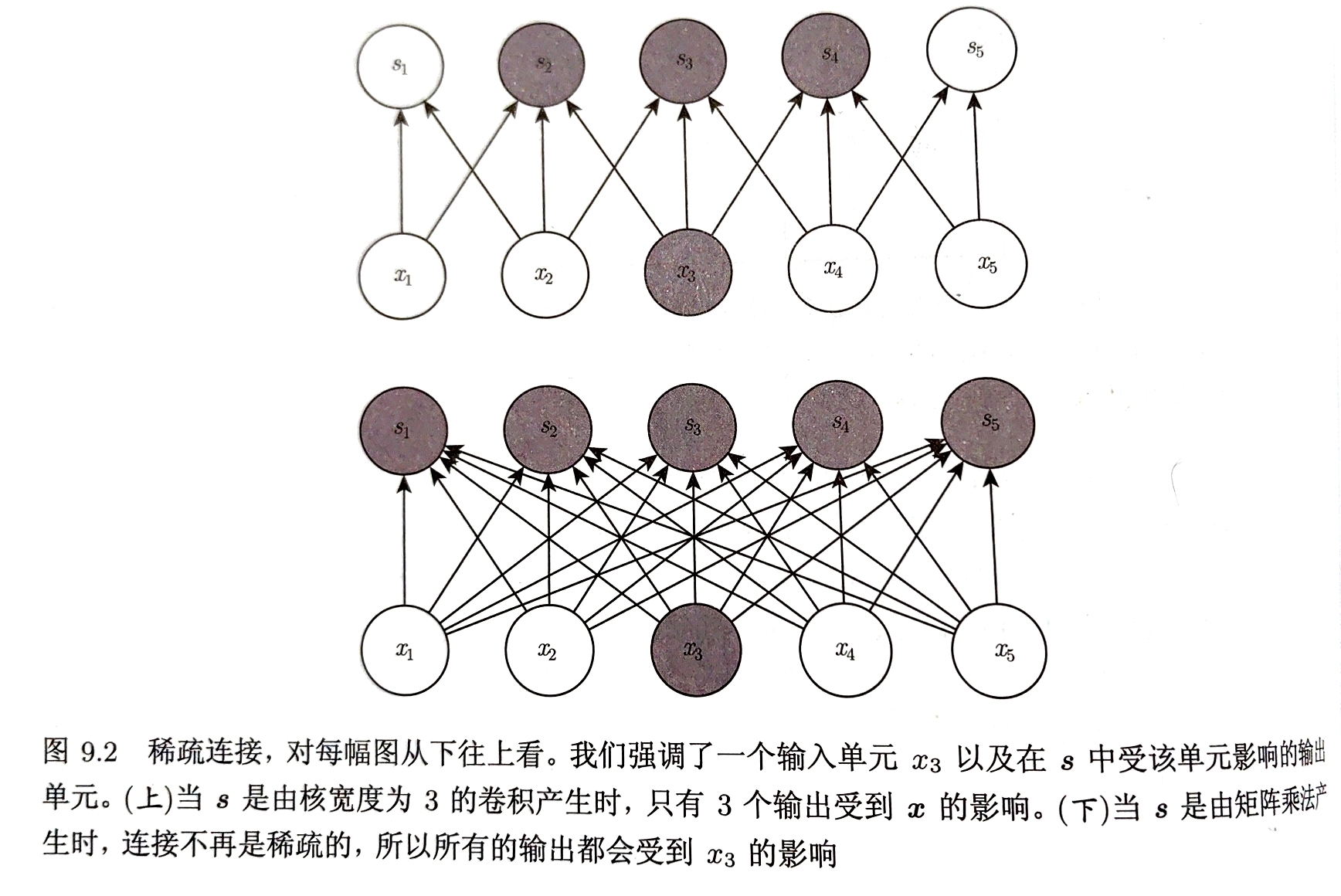
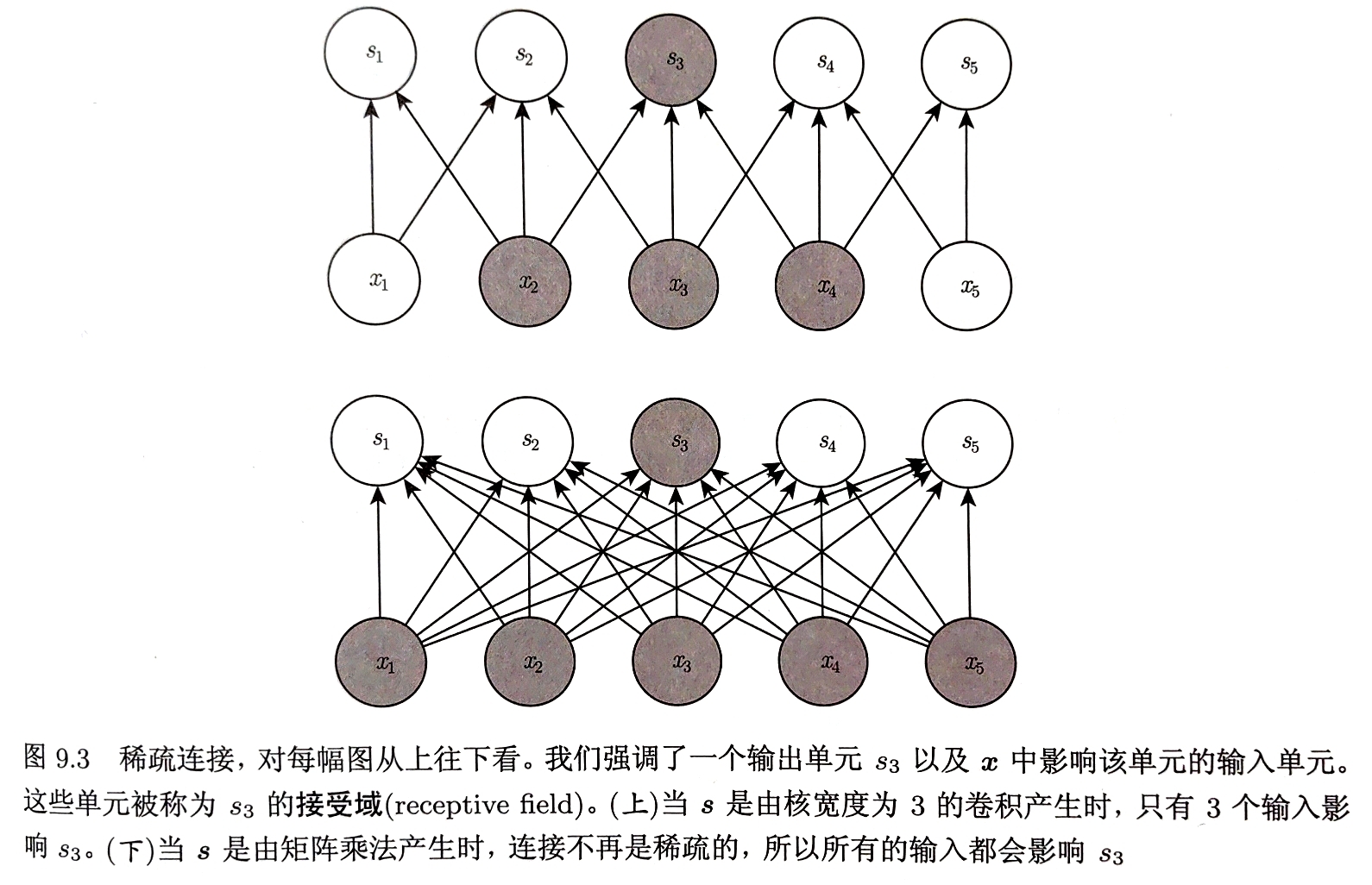
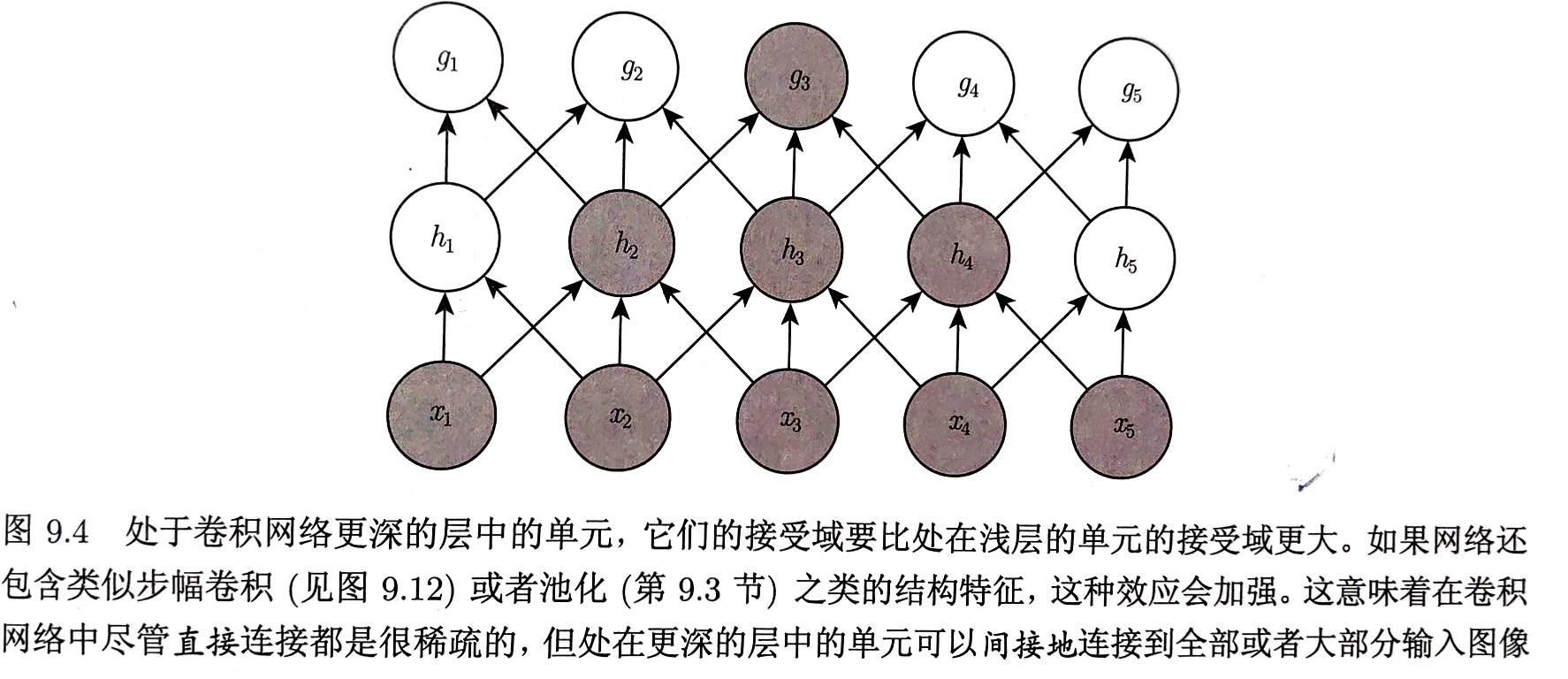
传统的神经网络使用矩阵乘法建立输入输出的连接关系,而卷积网络通过使用远小于输入大小的核使网络具有稀疏交互特征 为了得到输出只需很少的计算量,极大提高效率
|  |
|  |
|  |
参数共享
指在一个模型的多个函数中使用相同的参数 网络中含有绑定的权重
卷积神经网络中,核的每一个元素都作用在输入的每一个位置上 参数共享保证了只需学习一个参数集合 极大的降低了存储需求
等变表示
卷积参数共享的特殊形式使卷积神经网络具有平移等变的性质
等变:若一函数满足输入改变,输出也以同样的方式改变 $f(x)$对于变换$g$具有等变性:函数$f(x)$与$g(x)$满足$f(g(x))=g(f(x))$
对于卷积,若令$g$是输入的任意平移操作,那么卷积函数对于$g$具有可变性 若对函数$I$进行平移变换$g$然后进行卷积操作的结果与先对$I$进行卷积然后对输出使用平移函数$g$得到的结果一致
卷积对其他变换不是天然等变的,对图像的放缩、旋转变换需要特定的机制处理
池化
卷积神经网络中一个典型层包含三级:
- 并行计算多个卷积产生一组线性激活相应【卷积级-仿射变换】
- 每一个激活响应通过非线性的激活函数【探测级-非线性】
- 使用池化函数调整输出【池化级-近似不变性-特征提取】
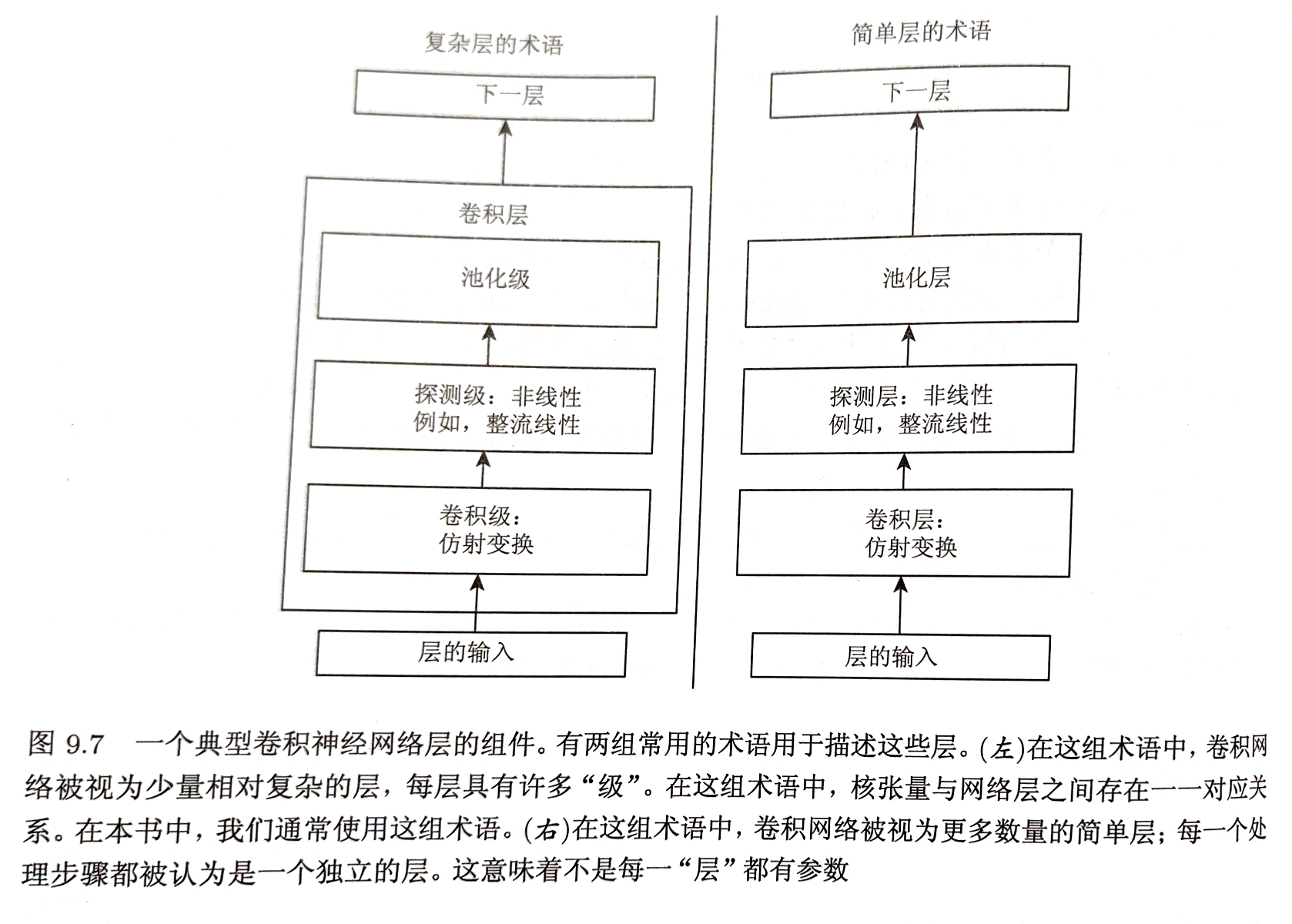
池化函数使用每一位置的相邻输出的总体统计特征来代替网络在该位置的输出
最大池化:给出相邻矩形区域内的最大值 均值池化:给出相邻矩形区域内的平均值 $L^{2}$范数池化 基于距中心像素距离的加权平均函数
当输入做出少量平移时,池化能够帮助输入的表示近似不变,即经过池化函数后的大多数输出并不会发生改变 局部平移不变性非常重要,特别是当我们关心某个特征是否出现而不关心出现的具体位置
池化可看做一个无限强的先验:这一层学得的函数必须具有对少量平移的不变性
当假设成立时,池化可以极大提高网络的统计效率
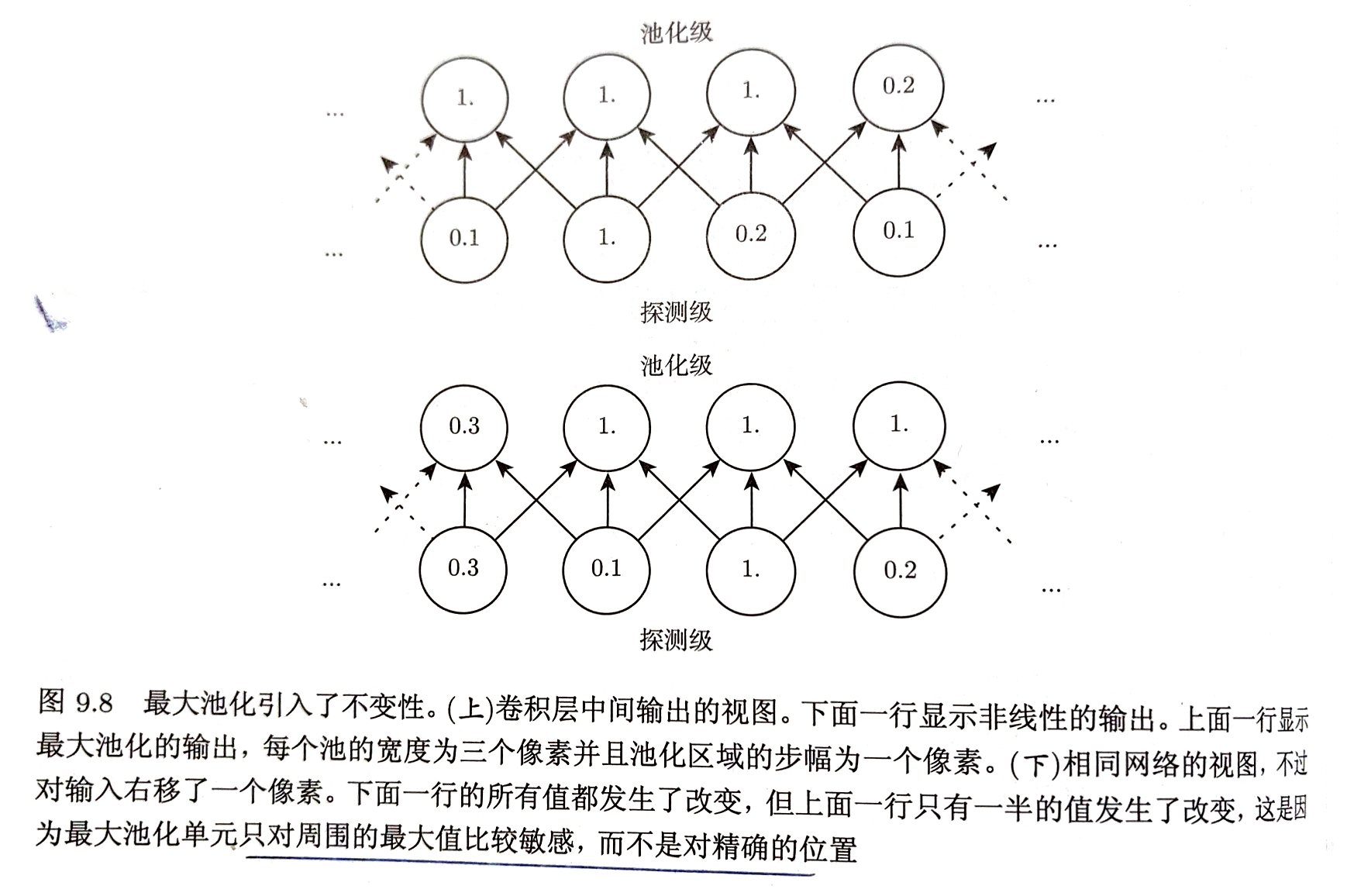
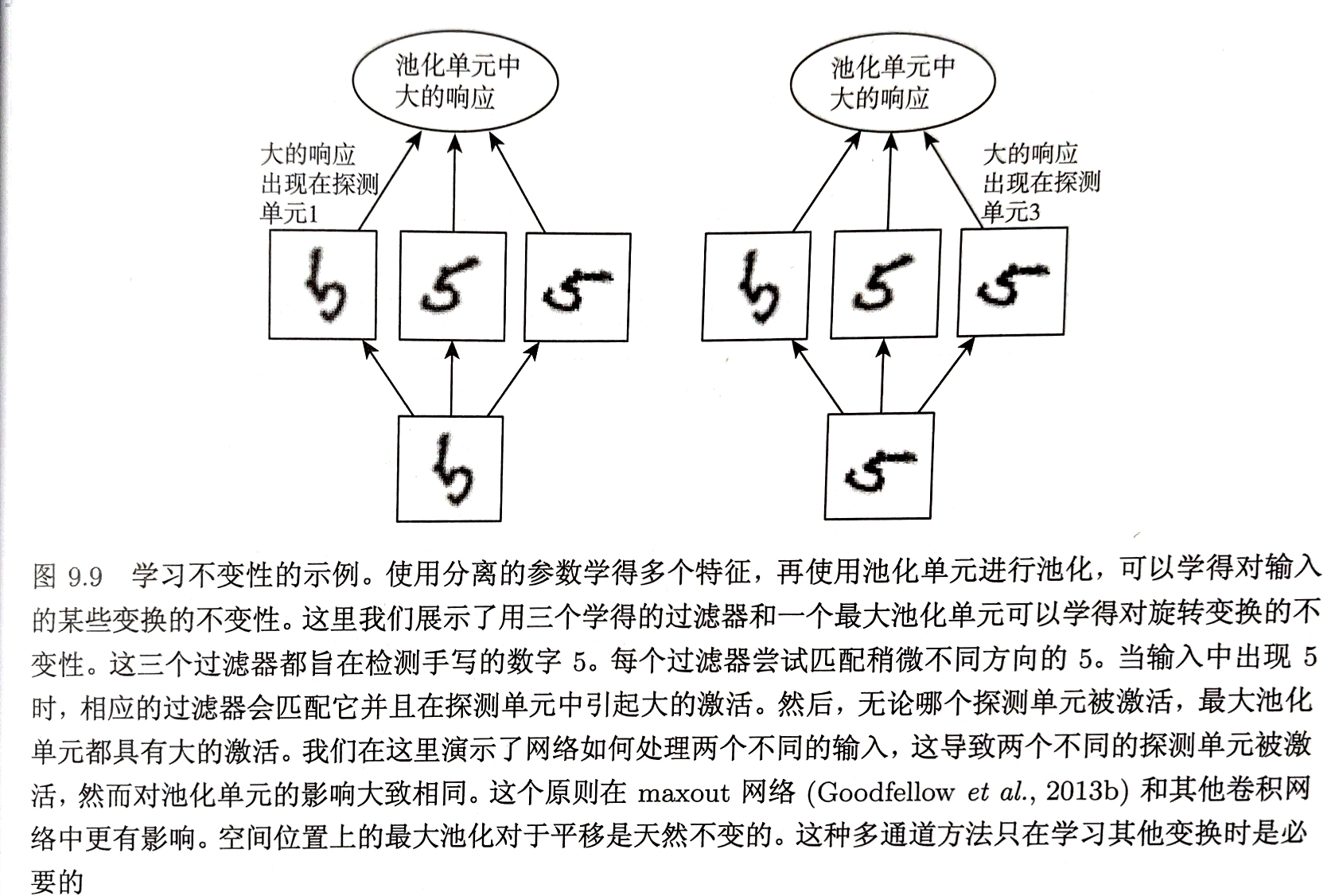
池化综合了全部邻居的反馈,使得池化单元少于探测单元成为可能
将下一层减少$k$倍的输入提高了网络的计算效率
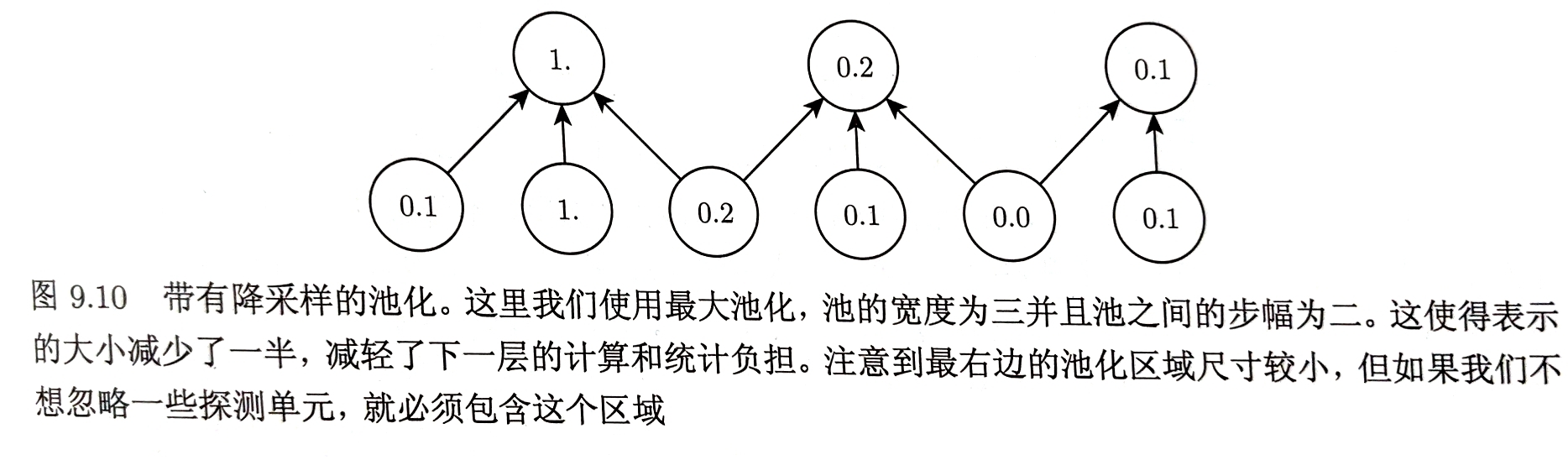
池化能够处理大小不同的输入 如对图像分类时,分类层的输入必须是固定大小的,通常需要通过调整池化区域的偏置大小实现,这样分类层总是能够接收到相同数量的统计特征而不论初始输入大小
卷积神经网络可视作具无限强的只包含局部连接关系并且对平移具有不变性的先验 要求一个隐藏单元的权重必须与邻居权重相同 除在隐藏单元的小的空间连续的接受域内的权重外,其余权重为0 池化是每一个单元都具有对少量平移的不变性的先验
卷积和池化可能导致欠拟合:先验假设不正确 若任务依赖保存精确的空间信息,在所有特征上使用池化会增大训练误差 一些卷积网络结构为既获得具有较高不变性的特征有获得平移不变性不合理时不会导致欠拟合的特征,被设计成在一些通道上使用池化而在另一些通道上不使用
基本卷积函数的变体
神经网络中的卷积通常指由多个并行卷积组成的运算 具有单个核的卷积只能提取一种类型的特征,我们希望网络的每一层能够在多个位置提取多种类型的特征
处理图像时,卷积输入输出通常看做3维张量,软件采用批处理模式故实际上使用4维张量,第4维索引用于标明批处理中不同实例
假设4维核张量$\mathbf{K}$元素$\mathsf{K}{i,j,k,l}$表明输出处于通道$i$的一个单元与输入处于通道$j$的一个单元的连接强度;在输出与输入单元之间有$k$行$l$列的偏置 假设输入有观测数据$\mathbf{V}$组成,元素为$\mathsf{V}{i,j,k}$表明处于通道$i$中第$j$行第$k$列的值 输出$\mathbf{Z}$是对$\mathbf{K}$和$\mathbf{V}$进行卷积的结果: \(\mathsf{Z}_{i,j,k}=\sum\limits_{l,m,n}\mathbf{V}_{i,j+m-1,k+n-1}\mathsf{K}_{i,l,m,n}\) 线性代数中,向量索引从1开始,故-1 **编程语言中简化为:$\mathsf{Z}{i,j,k}=\sum\limits{l,m,n}\mathbf{V}{i,j+m,k+n}\mathsf{K}{i,l,m,n}$
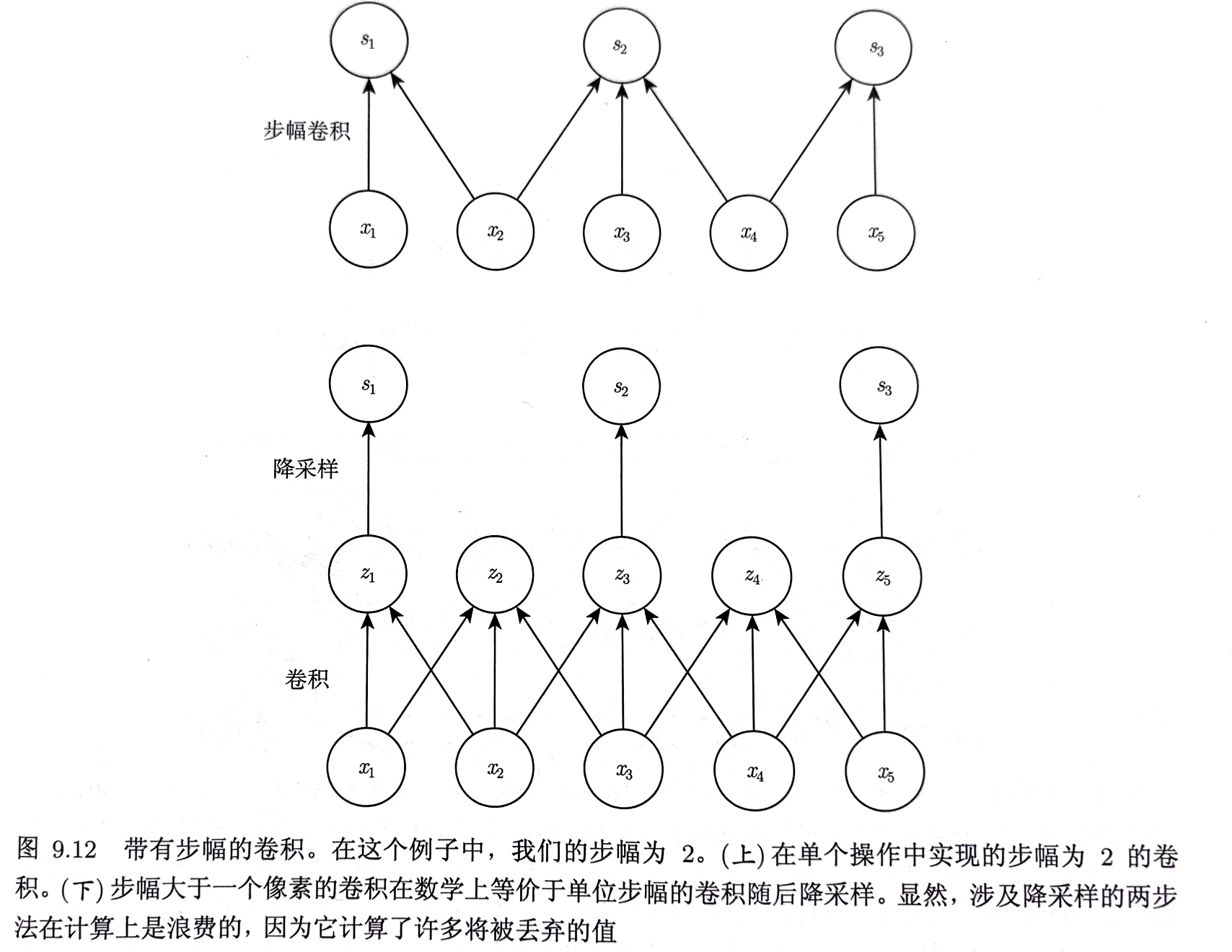
跳过核中的某些位置减少计算开销(代价为提取特征变弱)
在输出方向每间隔$s$个像素进行采样,下采样卷积函数$c$
$\mathsf{Z}{i,j,k}=c(\mathbf{K},\mathbf{V},s){i,j,k}=\sum\limits_{l,m,n}[\mathsf{V}{Pl,(j-1)\times s+m,(k-1)\times s+n},\mathsf{K}{i,l,m,n}]$
$s$为下采样卷积的步幅(stride)
零填充
卷积网能够隐含地对输入$\mathbf{V}$用0进行填充,使其加宽
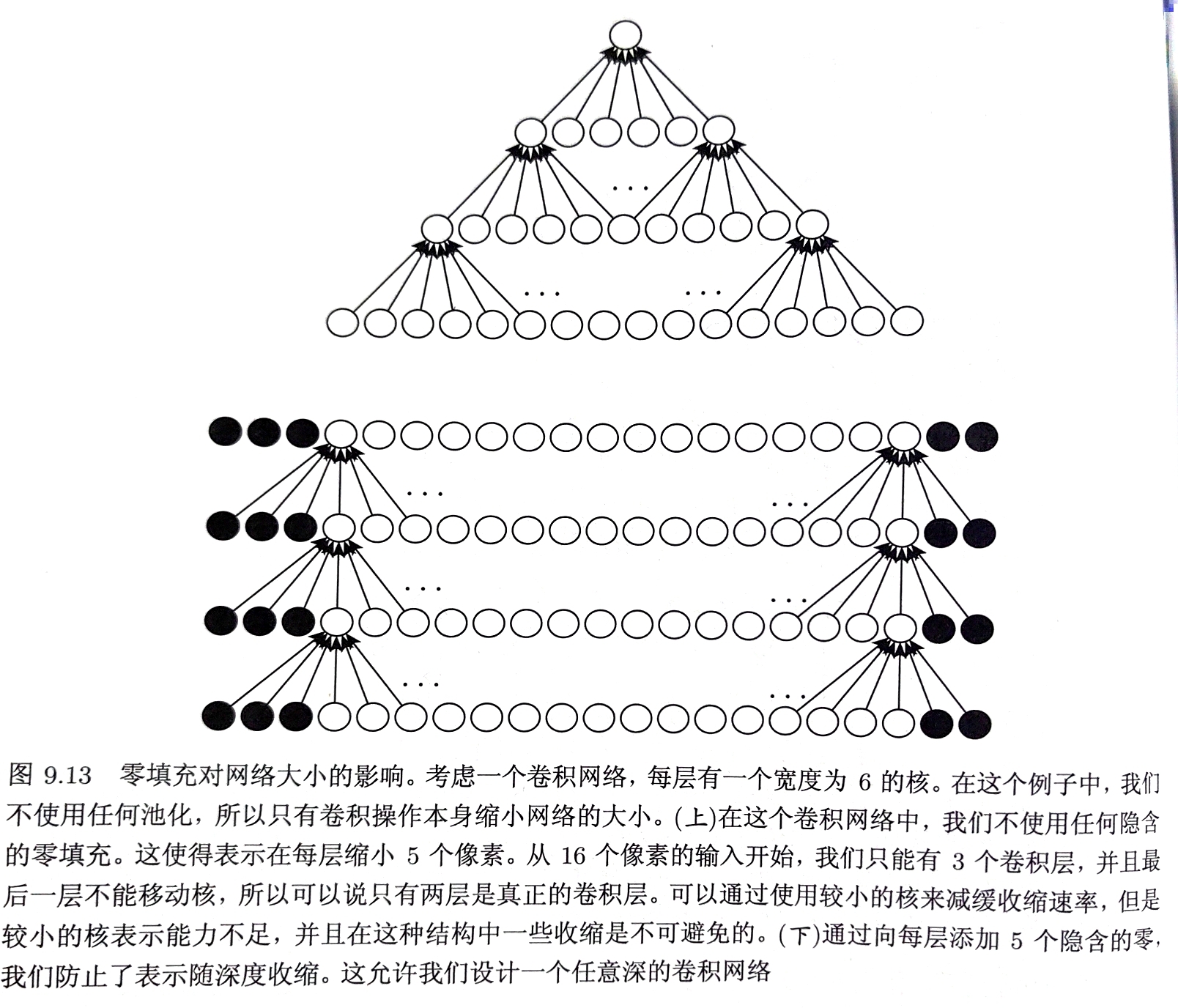
- 有效卷积(Valid)
- 不使用0填充
- 卷积核只允许访问能够完全被整个核包含的位置
- 输出大小每层按核的宽度$k-1$的速度减小
- 相同卷积(Same)
- 利用0填充使输入和输出保持相同大小
- 网络能够支持任意多的卷积层
- 输入像素中靠近边界的部分比中间部分对输出像素的影响更小——边界像素欠表示
- 全卷积(Full)
- 进行充分的0填充
- 每个像素在每个方向上被访问$k$次,输出图像宽度$m+k-1$
- 输出像素中靠近边界的部分相比中间部分是更小像素的函数
- 学得一个在卷积特征映射的所有位置都表现不错的单核更为困难
通常零填充的最优数量介于Valid卷积和Same卷积之间
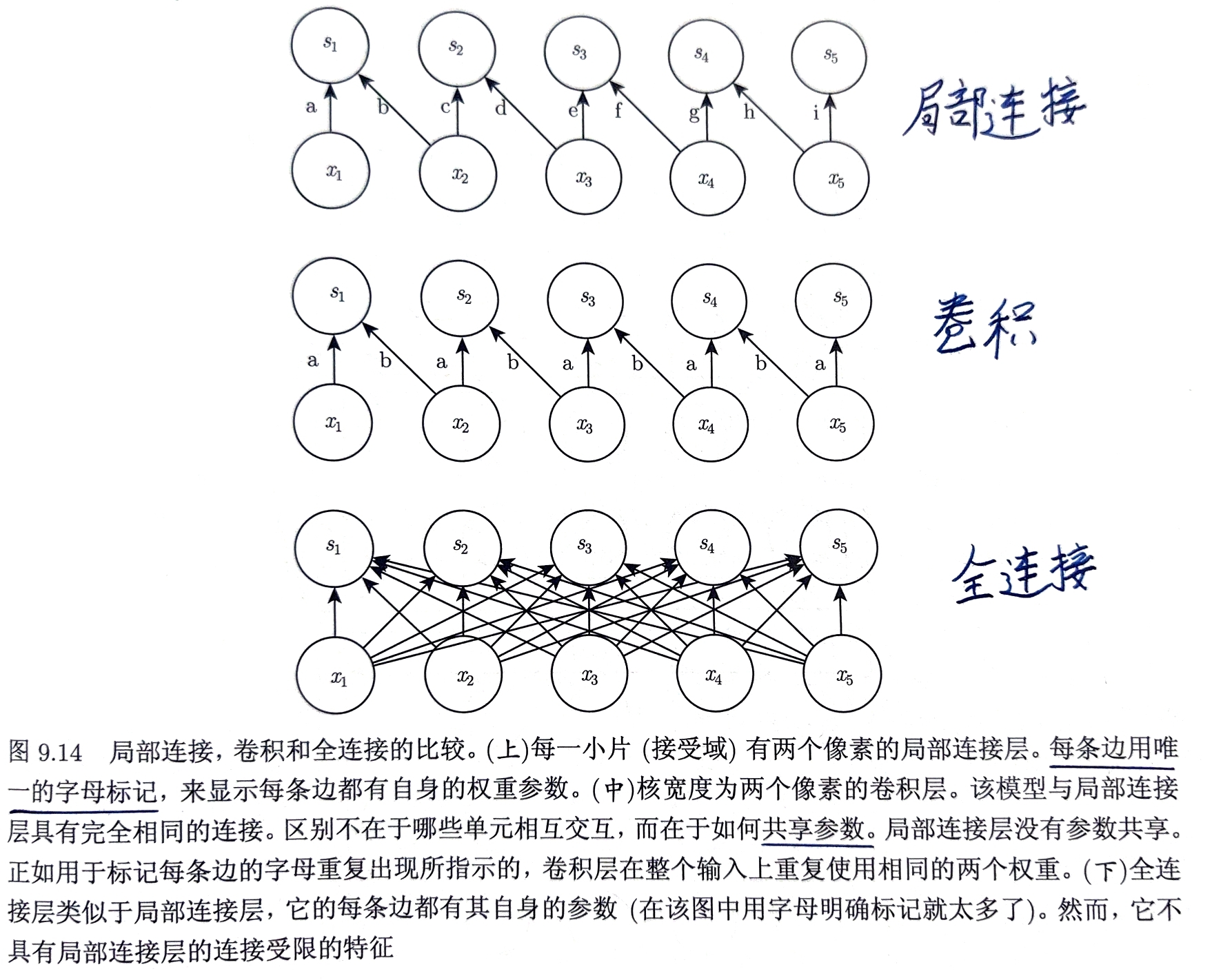
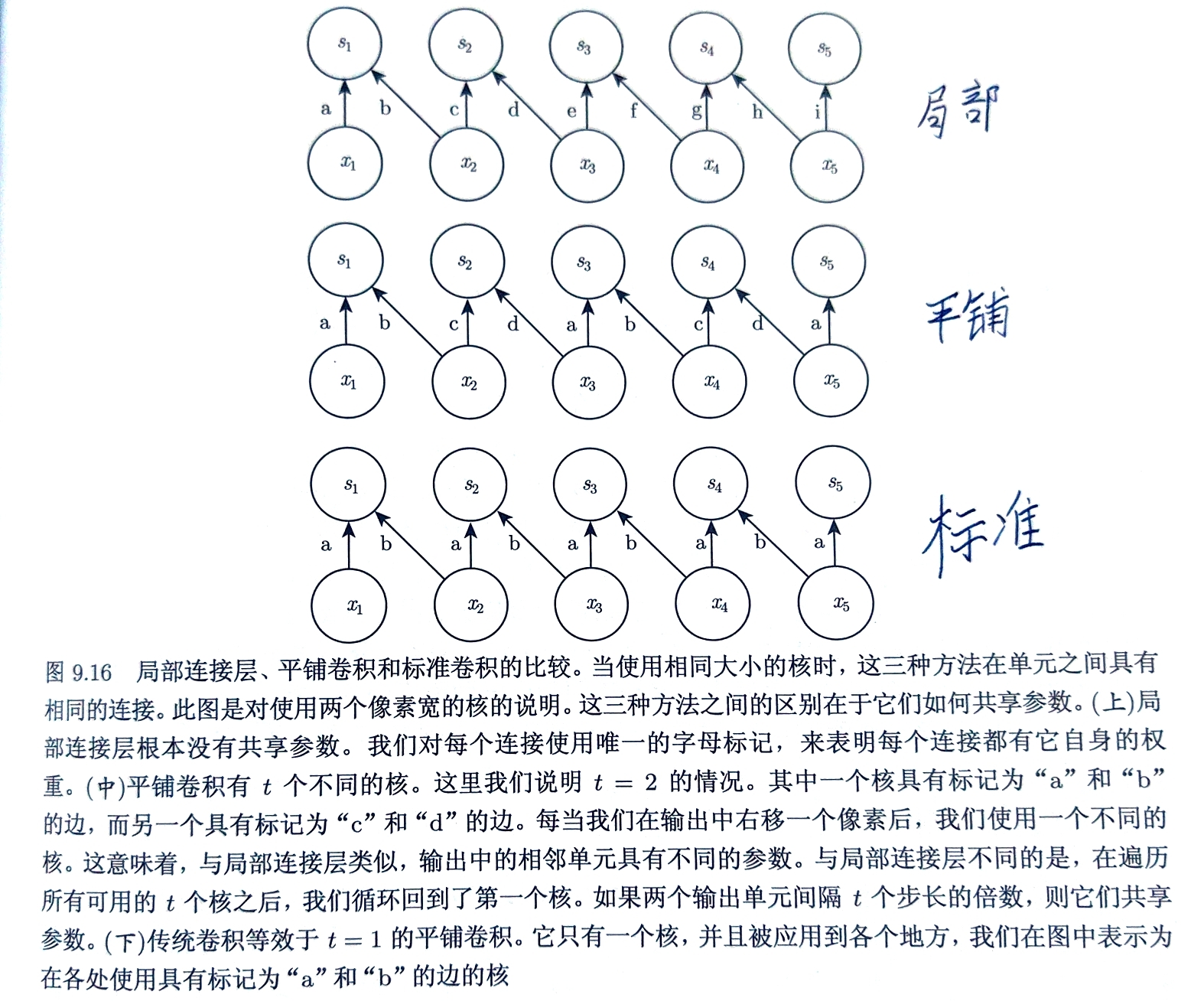
非共享卷积:局部连接
与卷积类似,但每个连接有自己的权重,参数不共享 使用6维张量$\mathbf{W}$表示,索引为输出通道$i$,输出行$j$列$k$,输入通道$l$,输入行偏置$m$、列偏置$n$ 局部连接的线性部分:$\mathsf{Z}{i,j,k} = \sum\limits{l,m,n}[\mathsf{V}{l,j+m-1,k+n-1}w{i,j,k,l,m,n}]$ 当每个特征都是一小块空间的函数并且相同的特征不会出现在所有的空间上时采用局部连接层 例:辨别人脸图像只需寻找嘴是否在图像下半部分
|  |
平铺卷积
对卷积层和局部连接进行折中 学习一组核使在空间移动时可以循环利用 对参数的存储空间仅会增长核的集合大小倍
令$\mathbf{K}$为6维张量,索引不包含输出位置,输出位置在每个方向上在$t$个不同的核组成的集合中进行循环 $\mathsf{Z}{i,j,k}= \sum\limits{l,m,n} \mathsf{V}{l,j+m-1,k+n-1}\mathsf{K}{i,l,m,n,j\%t+1,k\%t+1}$ $\%$为取模运算 当$t=输出宽度$时为局部连接
|  |
运算与输出
使用大步幅的池化层导致输出平面比输入平面小
对图像逐个像素标记的一种策略是先产生图像标签的原始猜测,然后使用相邻像素之间的交互来修正原始猜想——重复修正对应每一步使用相同的卷积 一般的想法是大片相连的像素倾向于对应相同的标签
卷积处理可变尺寸的输入和输出
卷积等效于使用傅里叶变换将输入与核都转换到频域、执行两个信号的逐点相乘,在使用傅里叶变化转化回时域