第10章 序列建模：循环和递归网络
循环神经网络RNN是一类用于处理序列数据的神经网络 RNN可以扩展到很长的序列，大多数RNN能处理可变长度序列
参数共享使模型能够扩展到不同形式的样本（不同长度的样本）并进行泛化 当信息的特定部分在序列内多个位置出现时，参数共享尤为重要
时间序列上的卷积：时延神经网络 卷积允许共享网络跨时间共享参数，但是浅层的 参数共享体现在每个时间步中使用相同的卷积核
循环神经网络参数共享通过输出的每一项是前一项的函数 循环网络通常在序列的小批量上操作，并且小批量的每一项具有不同序列长度$\tau$
展开计算图
本质上任何涉及循环的函数都可视为一个循环神经网络
动态系统的经典形式 $s^{t}=f(s^{t-1};\theta)$ $s^{t}$称为系统的状态
由外部信号$x^{t}$驱动的动态系统 $s^{t}=f(s^{t-1},x^{t};\theta)$ 隐藏单元：$h^{t}=f(h^{t-1},x^{t};\theta)$
当循环网络根据过去预测未来，网络通常要学习使用$h^t$作为过去序列与任务相关方面的有损摘要 有损使其映射任意长度的序列$(x^t, x^{t-1},…,x^1)$到固定长度向量$h^t$ 根据不同的训练准则，摘要选择性地精确保留过去序列的某些方面
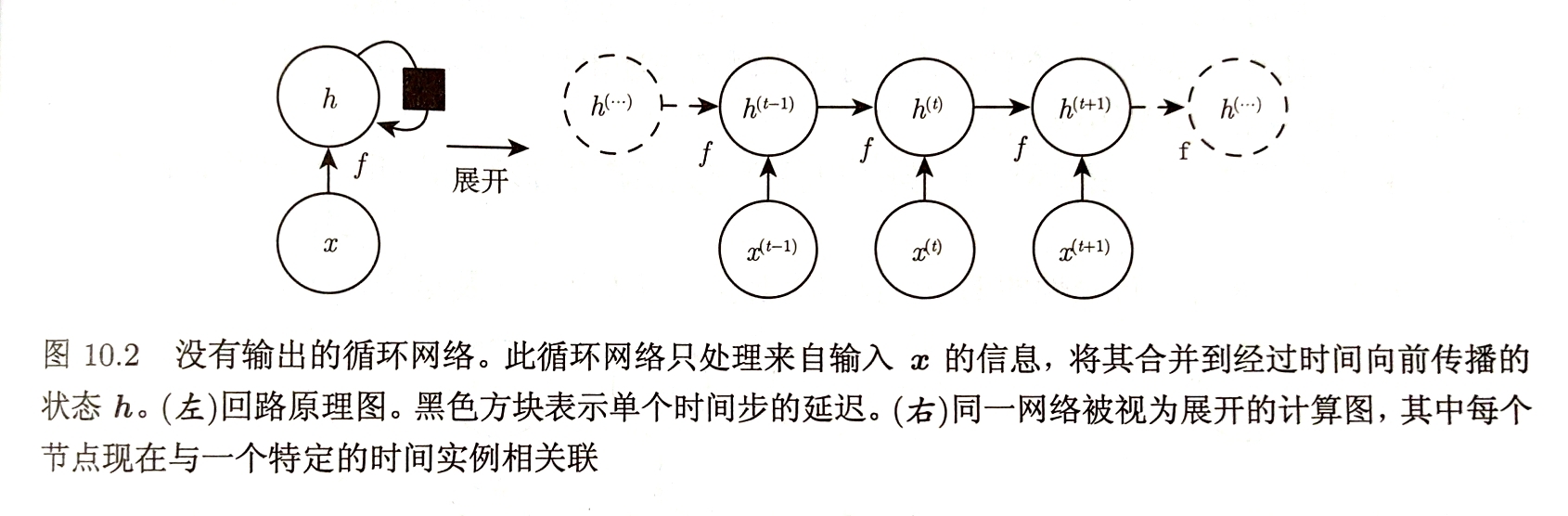展开：将左图回路映射为右图包含重复组件的计算图的操作
函数$g^{t}$代表经$t$步展开后的循环
$h^{t}=g^{t}(x^{t},x^{t-1},…,x^{1})=f(h^{t-1},x^{t};\theta)$
函数$g^{t}$将过去全部序列$(x^{t},x^{t-1},…,x^{1})$作为输入生成当前状态
展开的循环架构允许将$g^{t}$分解为函数$f$重复利用：
- 无论序列长度，学成的模型始终具有相同的输入大小
- 每个时间步使用相同参数的形同转移函数$f$
循环神经网络
RNN三种重要设计模式
- 每个时间步都有输出，并且隐藏单元之间有循环连接的循环网络
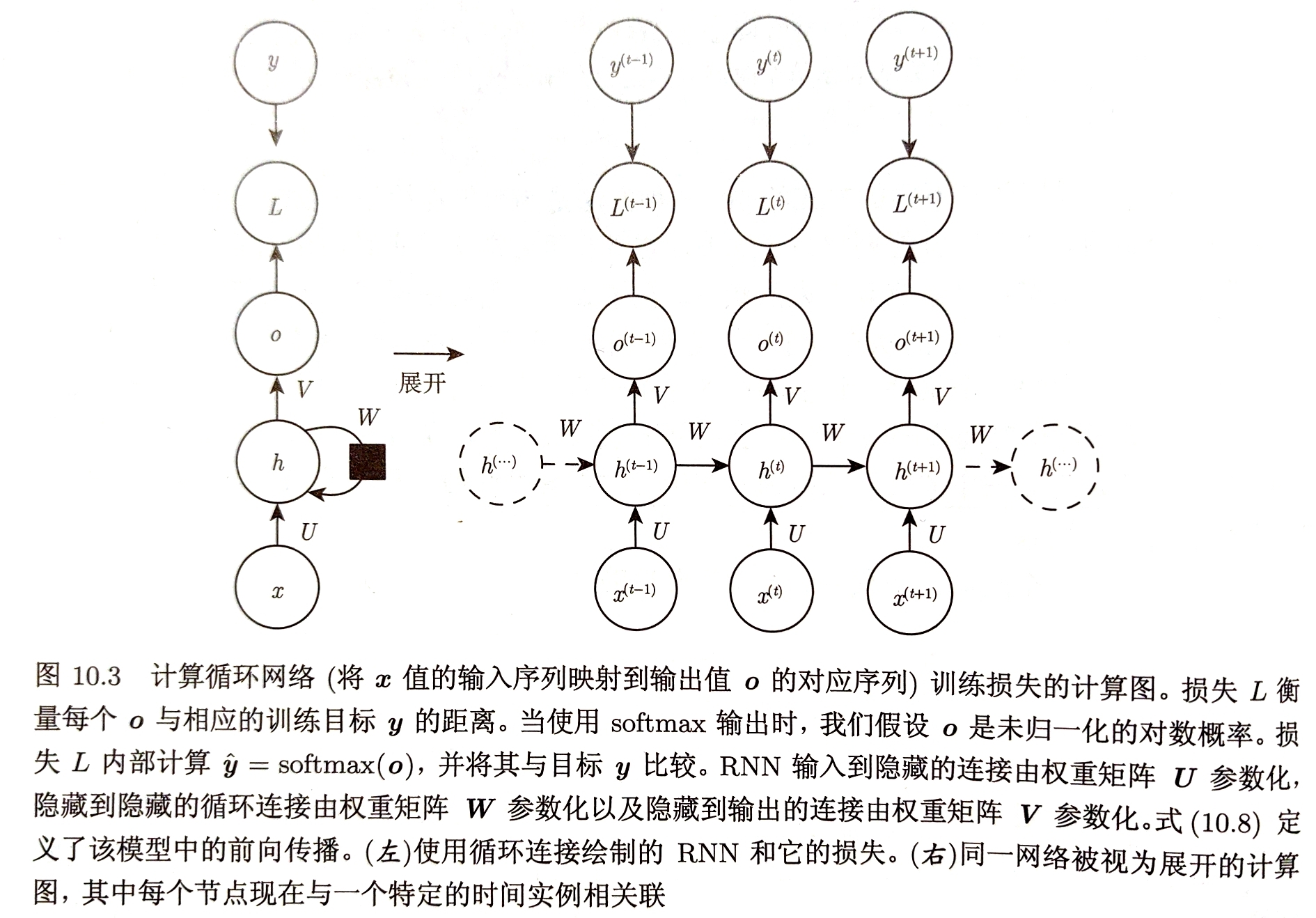假设使用双曲正切激活函数，输出离散（把输出$o$作为每个离散变量可能值的非标准化对数概率)，用softmax函数处理获得标准化后的输出向量$\hat{y}$
RNN从特定的初始状态$h^{0}$开始前向传播 更新方程：
- $a^{t}=b+Wh^{t-1}+Ux^{t}$【仿射】
- $h^{t}=tanh(a^{t})$【激活】
- $o^{t}=c+Vh^{t}$【隐藏-输出】
-
$\hat{y}^{t}=softmax(o^{t})$【转换输出】 总损失：所有时间步的损失之和 $\begin{aligned}L&({x^{1},…,x^{\tau}},{y^{1},…,y^{\tau}})\&=\sum\limits_{t}L^{t}\&=-\sum\limits_{t}log\ P_{model}(y^{t}|{x^{1},…,x^{t}})\end{aligned}$ 不能并行运算 前向传播中的各个状态必须保存 反向传播算法：通过时间反向传播 隐藏单元之间存在循环的网络非常强大但训练代价很大
-
每个时间步都产生一个输出，只有当前时刻的输出到下个时刻的隐藏单元之间有循环连接的循环网络
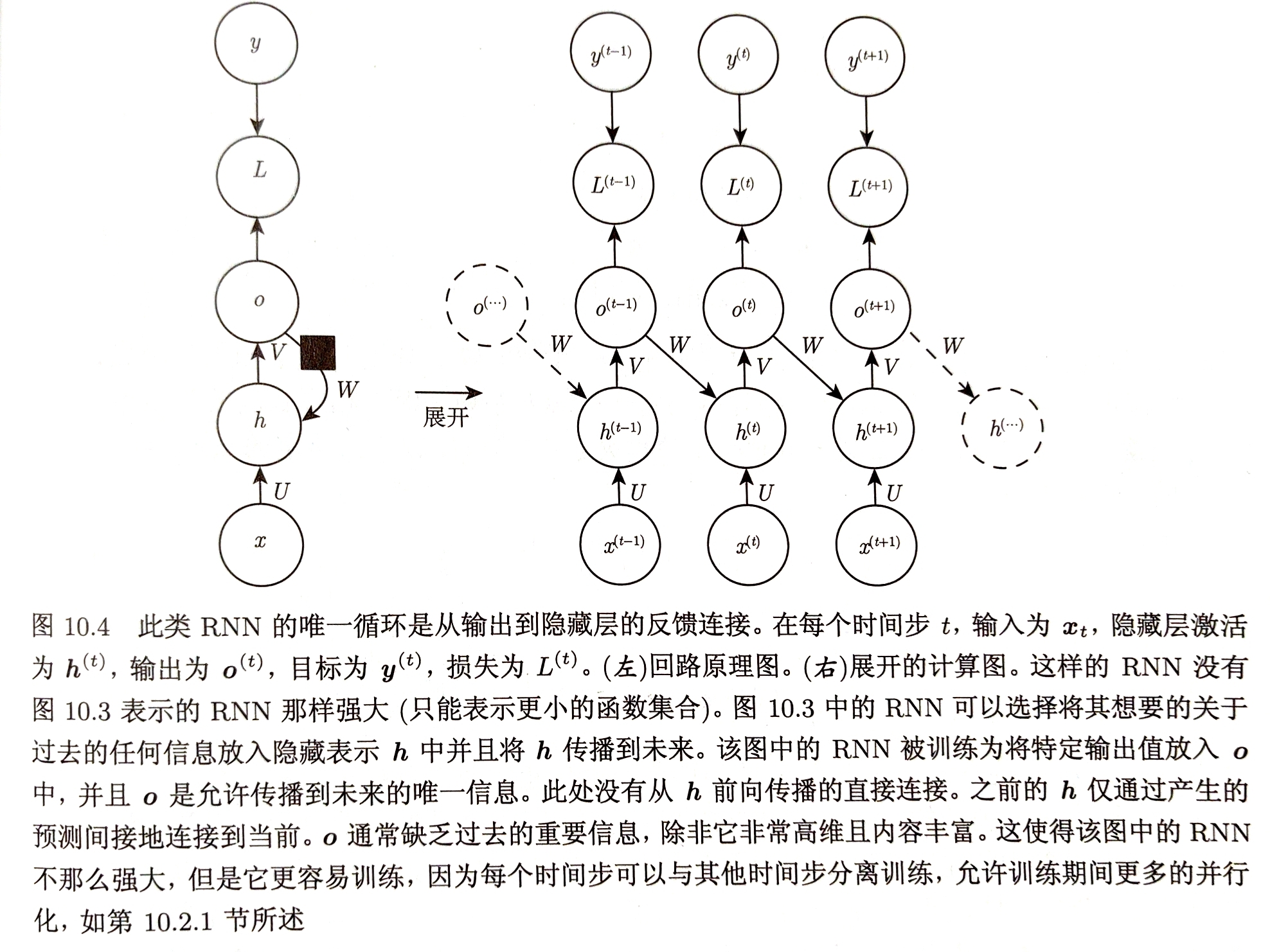消除隐藏到隐藏循环使所有时间步解耦，训练可并行化
使用导师驱动过程训练
在时刻$t+1$接受真实值$y^{t}$作为输入
条件最大似然准则
$\begin{aligned}&log\ P(y^{1},y^{2}|x^{1},x^{2})\=&log\ P(y^{2}|y^{1},x^{1},x^{2})+log\ P(y^{1}|x^{1},x^{2})\end{aligned}$
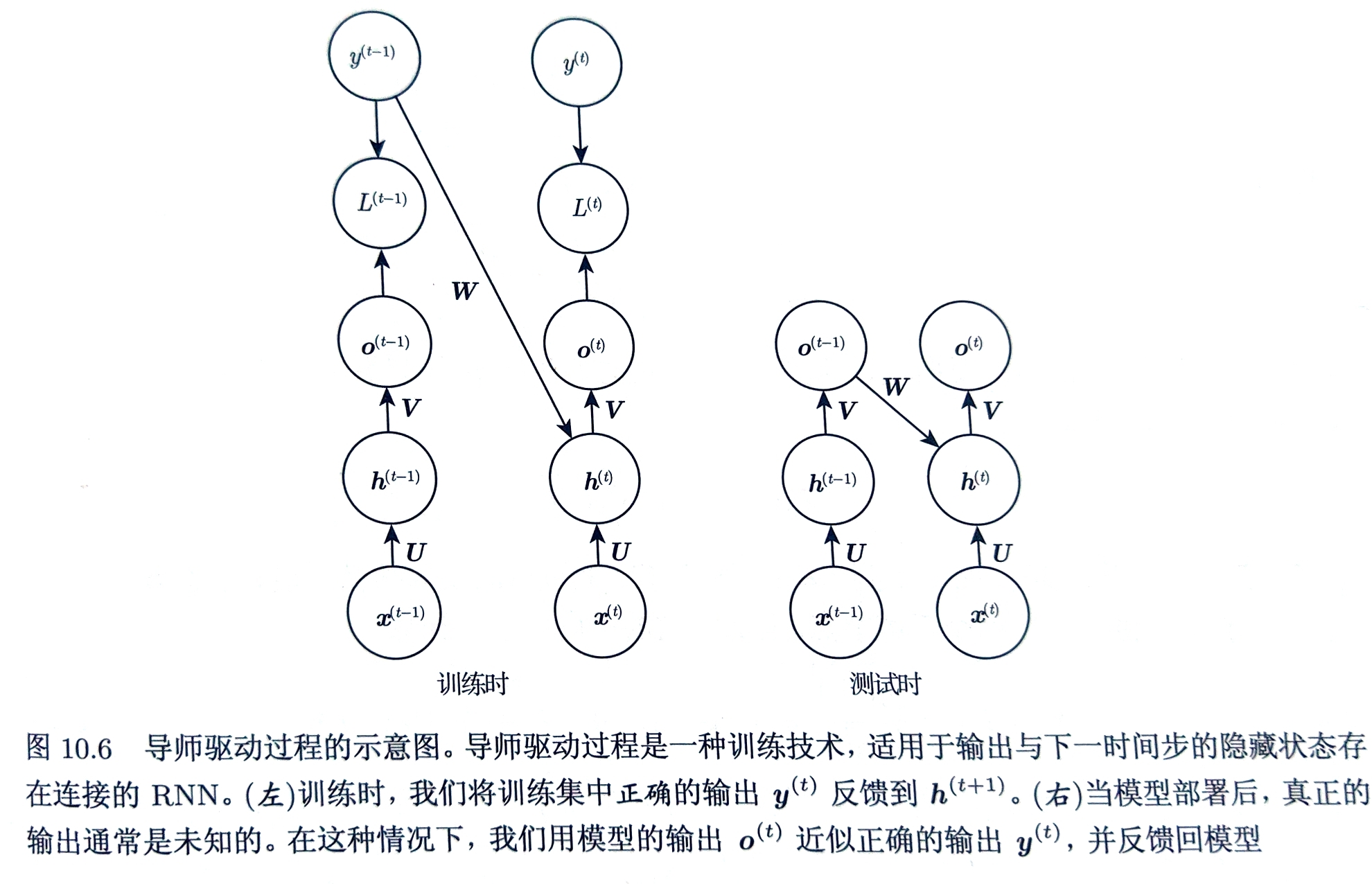导师驱动过程的最初动机为在缺乏隐藏到隐藏连接的模型中避免通过时间反向传播BPTT
但只要隐藏单元成为较早时间步的函数，BPTT应与导师驱动同时使用 - 隐藏单元之间存在循环连接，但读取整个序列后产生单个输出的循环网络!
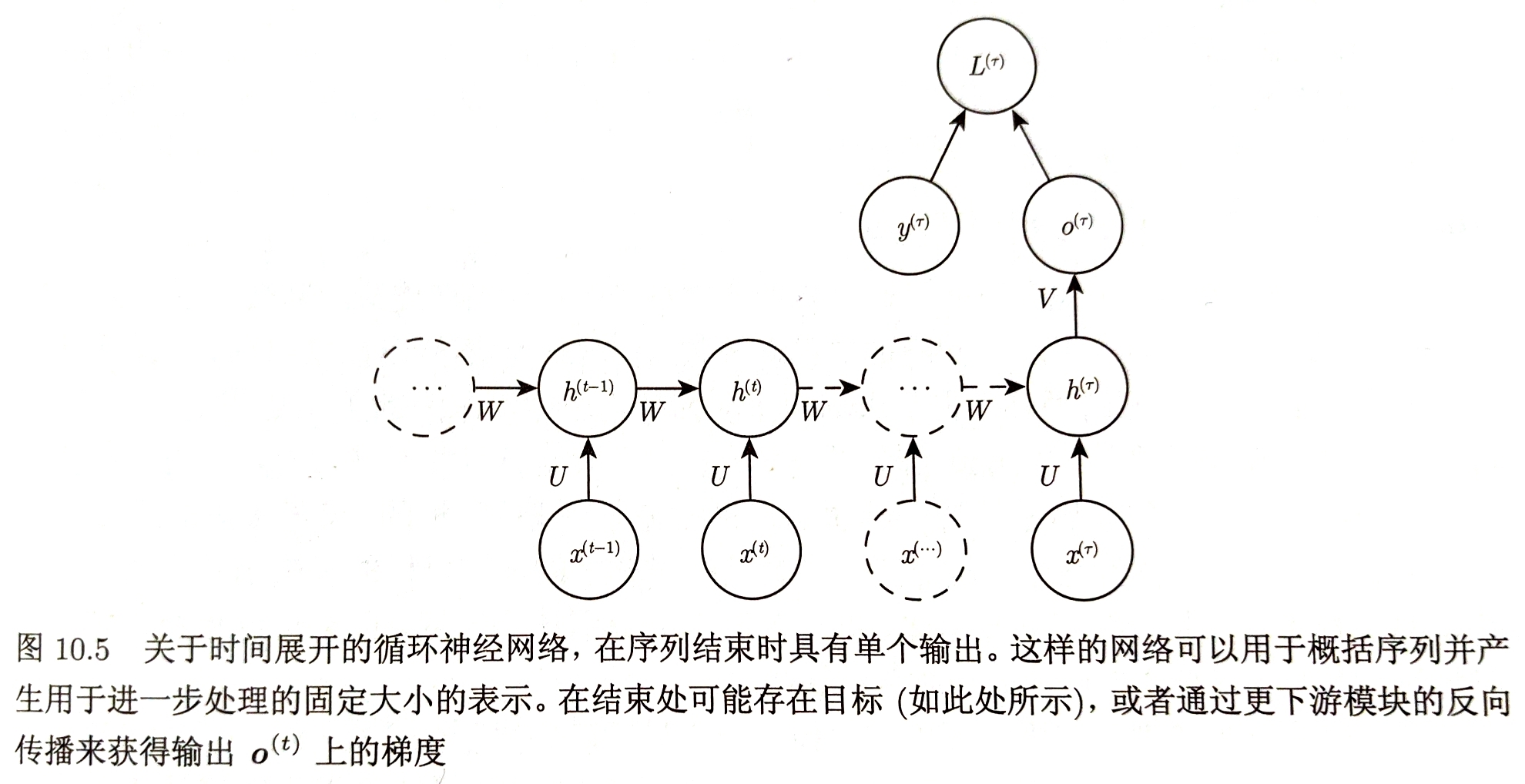
RNN梯度计算
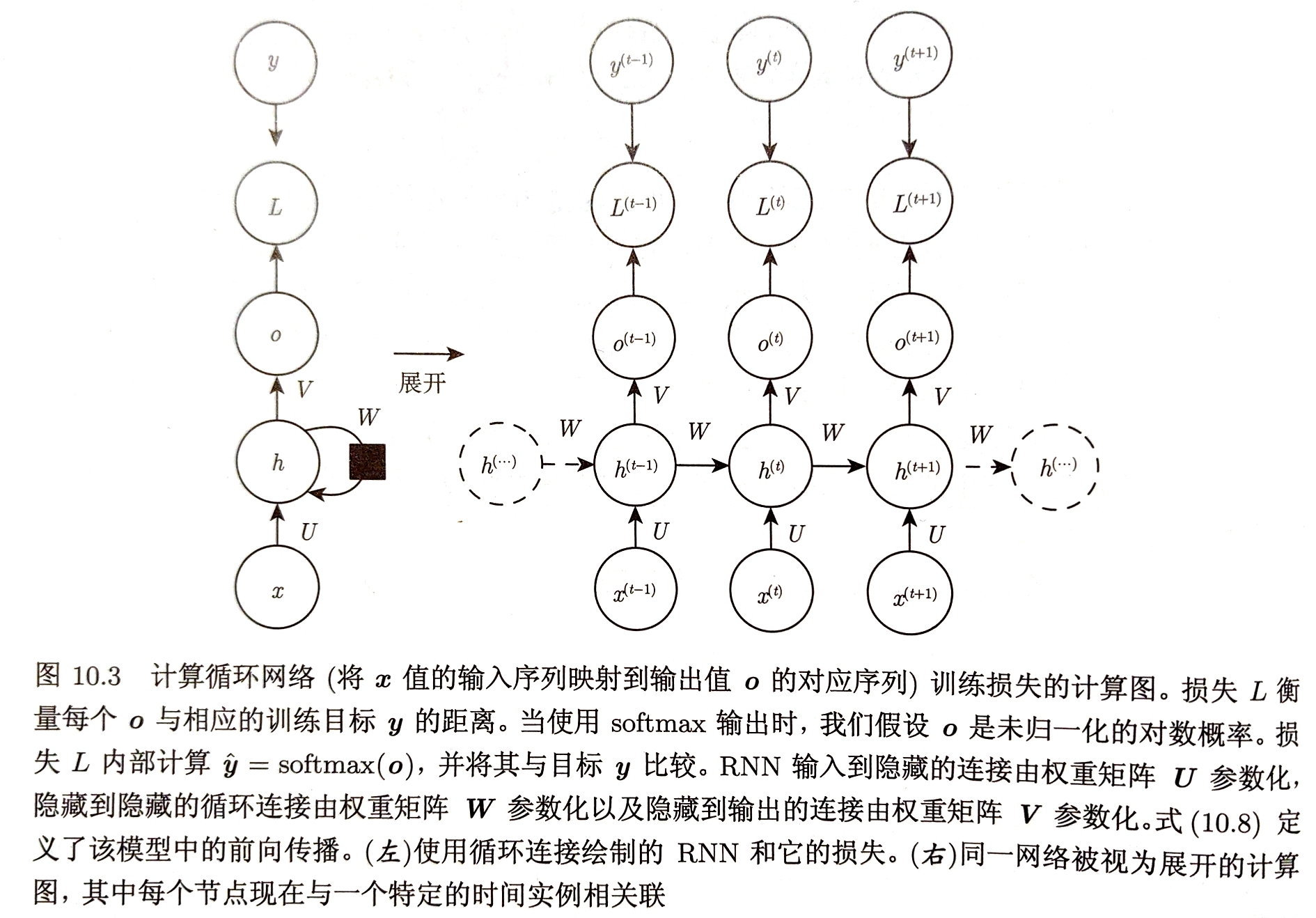
- $a^{t}=b+Wh^{t-1}+Ux^{t}$【仿射】
- $h^{t}=tanh(a^{t})$【激活】
- $o^{t}=c+Vh^{t}$【隐藏-输出】
- $\hat{y}^{t}=softmax(o^{t})$【转换输出】
对每个节点$\mathbf{N}$需要基于$\mathbf{N}$后面节点的梯度 从最终损失的节点开始递归$\frac{\partial L}{\partial L^{t}}=1$ 假设输出$o^{t}$为softmax函数的参数，损失是$y^{t}$的负对数似然 关于时间步$t$输出的梯度$\bigtriangledown_{o^{t}}L= \frac{\partial L}{\partial o_{i}^{t}}= \frac{\partial L}{\partial L^{t}} \frac{\partial L^{t}}{\partial o_{i}^{t}}=\hat{y}{i}^{t}-\mathbf{1}{i,y^{t}}$ 在最后时间步$\tau$，$h^\tau$只有$o^{\tau}$作为后续节点$\bigtriangledown_{h^{\tau}}L=\mathbf{V}^{\top}\bigtriangledown_{o^{\tau}}L$
则对一般的$h^{t}$同时具$o^{t}$和$h^{t+1}$两个后续节点 梯度：$\begin{aligned}\bigtriangledown_{h^{t}}L&=( \frac{\partial h^{t+1}}{\partial h^{t}})^{\top}(\bigtriangledown_{h^{t+1}}L)+(\frac{\partial o^{t}}{\partial h^{t}})^{\top}(\bigtriangledown_{o^{t}}L)\&=\mathbf{W}^{\top}(\bigtriangledown_{h^{t+1}}L)diag(1-(h^{t+1})^{2})+\mathbf{V}^{\top}(\bigtriangledown_{o^{t}L})\end{aligned}$ 其中$diag(1-(h^{t+1})^{2})$表示包含元素$1-(h_{i}^{t+1})^{2}$的对角阵，为时刻$t+1$与隐藏单元$i$关联的双曲正切的Jacobian
由于参数共享： $\bigtriangledown_{c}L=\sum\limits_{t}(\frac{\partial o^{t}}{\partial c})^{\top}\bigtriangledown_{o^{t}}L=\sum\limits_{t}\bigtriangledown_{o^{t}}L$ $\bigtriangledown_{b}L=\sum\limits_{t}(\frac{\partial h^{t}}{\partial a^{t}}\frac{\partial a^{t}}{\partial b^{t}})^{\top}\bigtriangledown_{h^{t}}L=\sum\limits_{t}diag(1-h^{t})^{2}\bigtriangledown_{h^{t}}L$ $\bigtriangledown_{V}L=\sum\limits_{t}\sum\limits_{i}(\frac{\partial L}{\partial o_{i}^{t}})\bigtriangledown_{V}o_{i}^{t}=\sum\limits_{t}(\bigtriangledown_{o^{t}}L)(h^{t})^{\top}$ $\bigtriangledown_{W}L=\sum\limits_{t}\sum\limits_{i}(\frac{\partial L}{\partial h_{i}^{t}})\bigtriangledown_{w^{t}}h_{i}^{t}=\sum\limits_{t}diag(1-(h^{t})^{2})(\bigtriangledown_{h^{t}}L)(h^{t-1})^{\top}$ $\bigtriangledown_{U}L=\sum\limits_{t}\sum\limits_{i}(\frac{\partial L}{\partial h_{i}^{t}})\bigtriangledown_{U^{t}}h_{i}^{t}=\sum\limits_{t}diag(1-(h^{t})^{2})(\bigtriangledown_{h^{t}}L)(x^{t})^{\top}$
有向图模型
RNN作为有向图模型，图模型中的边表示向量直接依赖于其他变量
许多图模型的目标是省略不存在强相互作用的边以实现统计和计算的效率
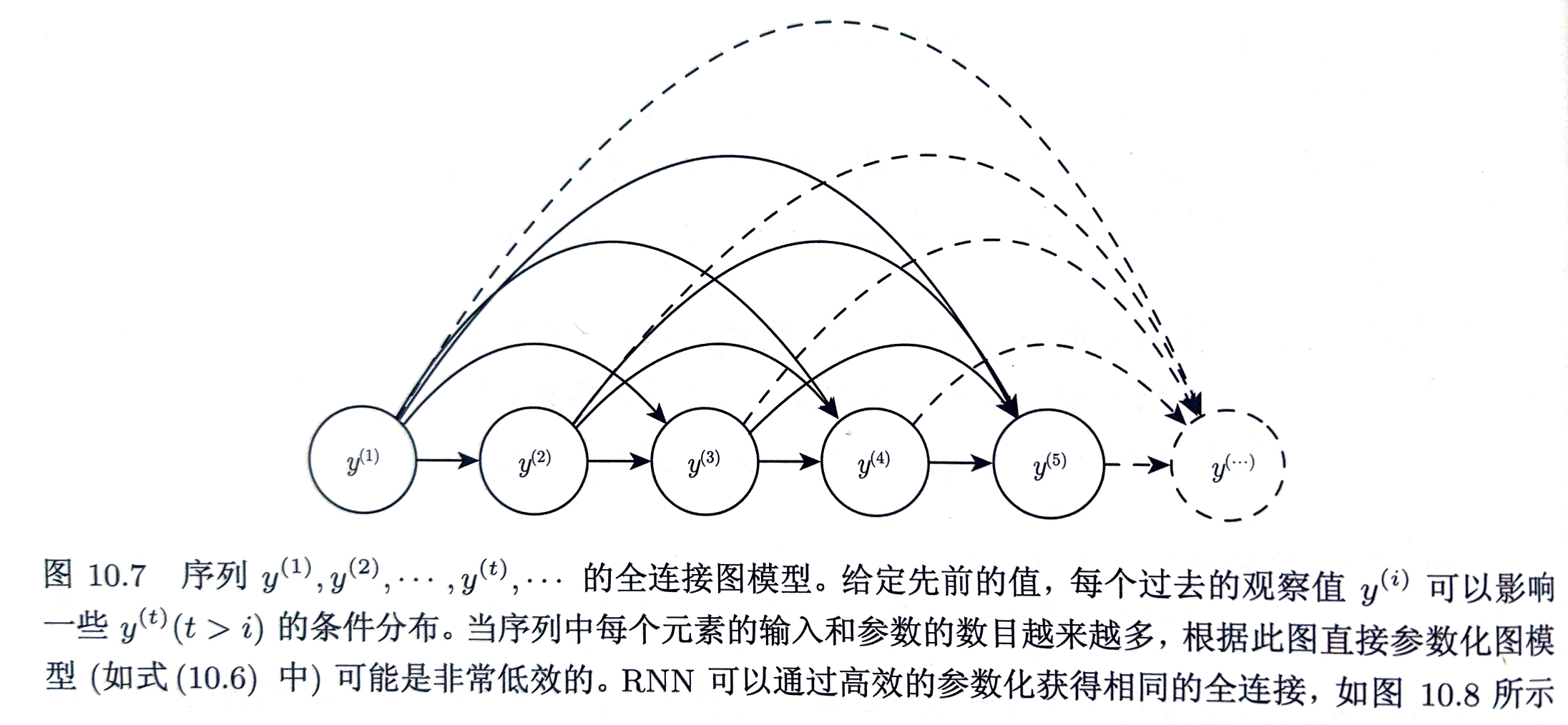循环网络为减少参数目的付出的代价是优化参数困难
参数共享的前提假设：相同参数可用于不同时间步
假设给定时刻$t$的变量后，时刻$t+1$变量的条件概率分布是平稳的
输入额外变量
- 在每个时刻作为一个额外输入
- 作为初始状态$h^{0}$
- 二者结合
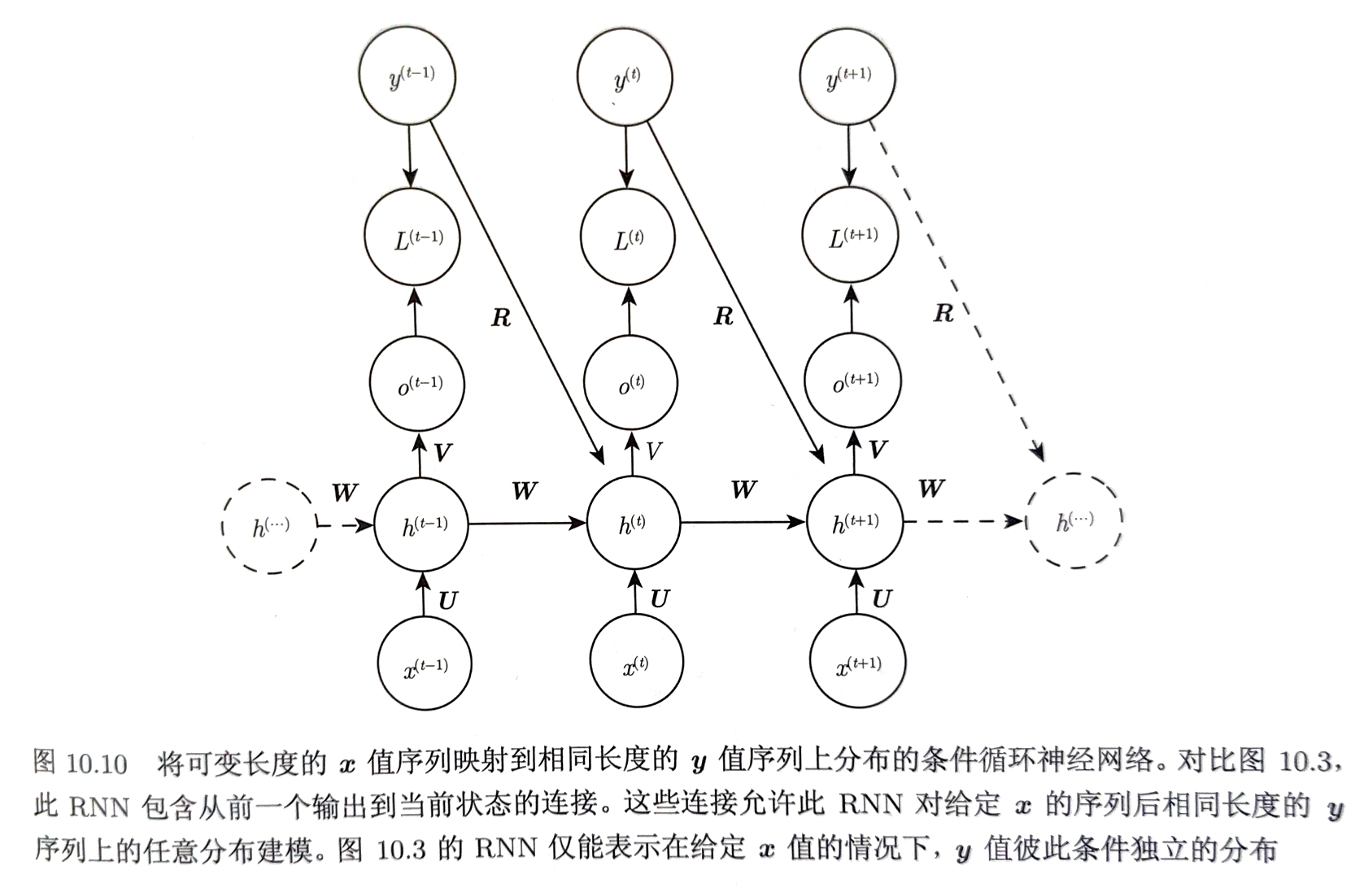
双向RNN
输出的预测依赖于整个输入序列，而非仅去信息 前馈网络、卷积网络或具有固定大小的先行缓存器的常规RNN需要指定$t$周围固定大小的窗口
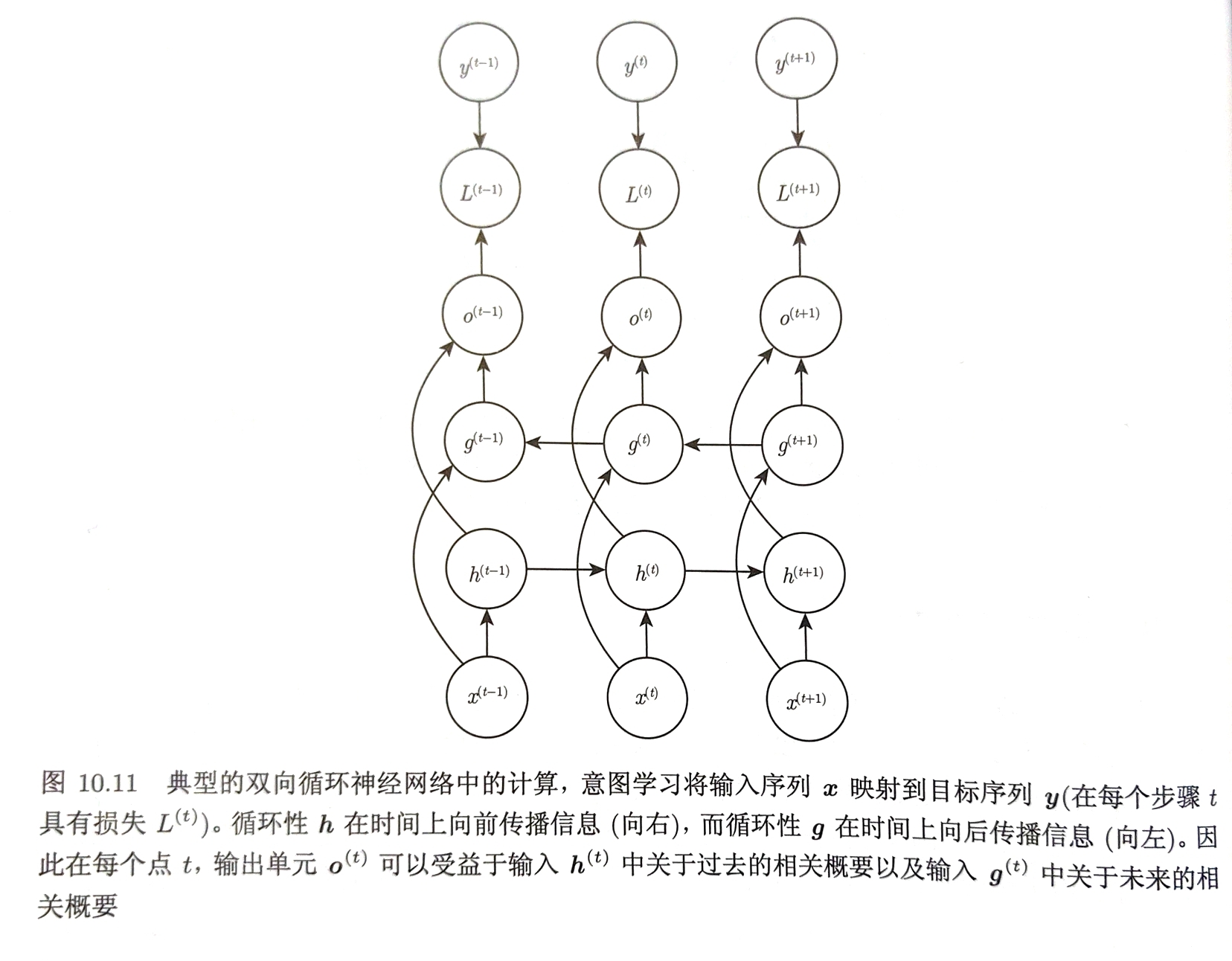
双向RNN结合时间上从序列起点开始移动的RNN和另一个时间上从序列末尾开始移动的RNN
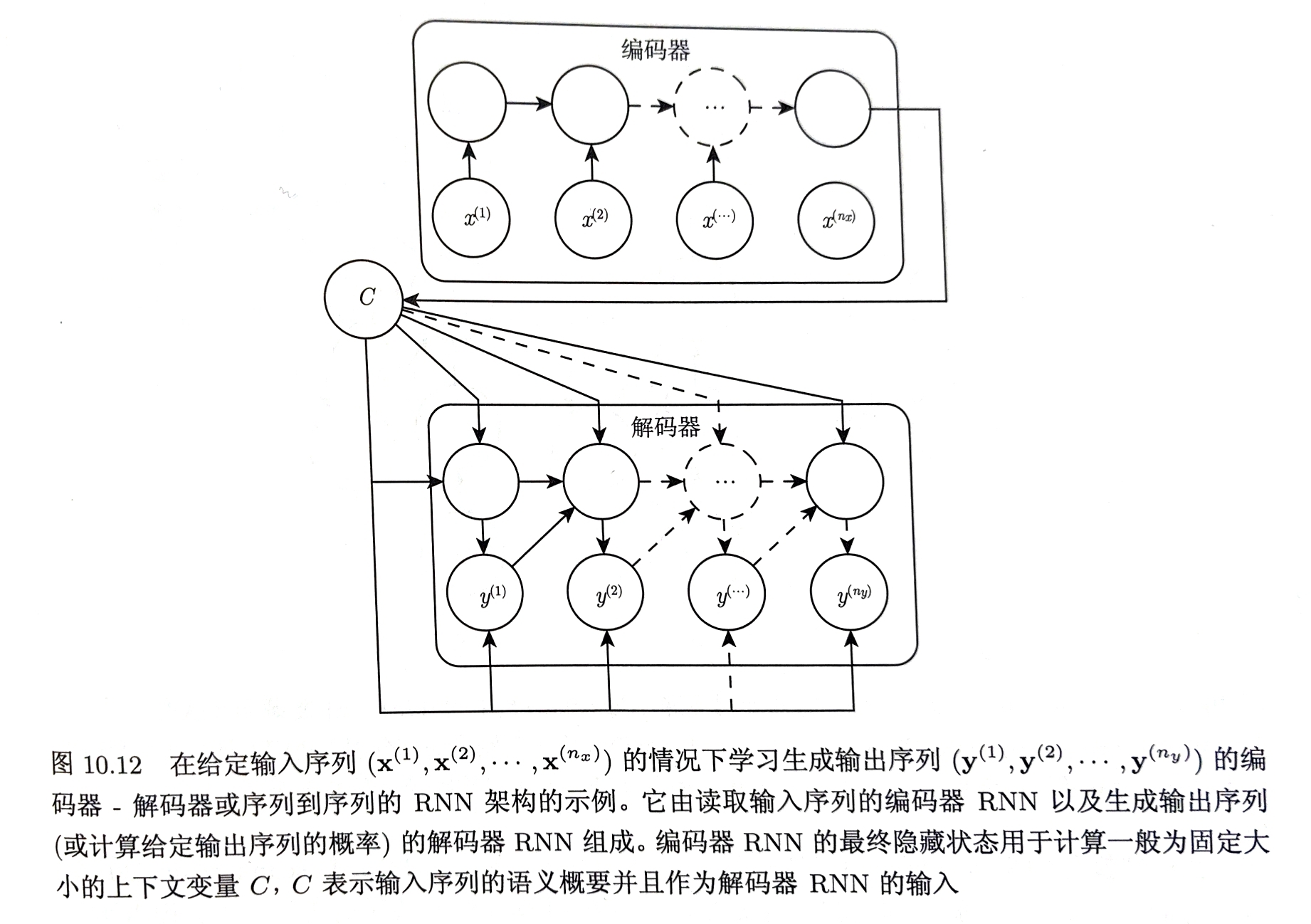
基于编码-编码的序列到序列架构
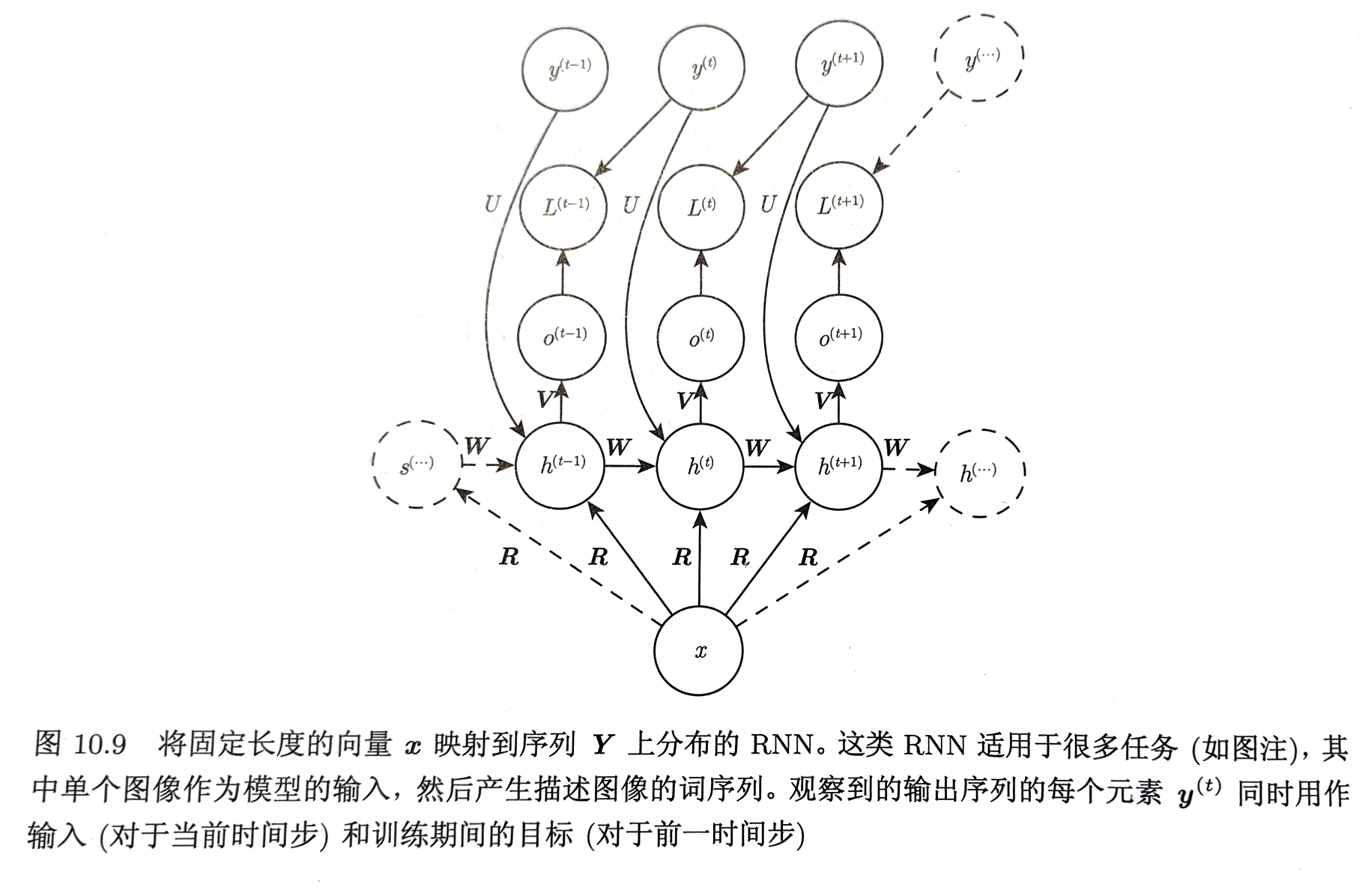
令RNN将输入序列映射到不一定等长的输出序列
上下文：RNN的输入 C：上下文的表示
框架：
- 编码器：输出上下文C
- 解码器：以固定长度的向量为条件产生输出序列$\mathbf{Y}=(y^{1},…,y^{n_{y}})$
两个RNN共同训练，编码器RNN最后一个状态$h_{n_{x}}$通常被当做输入的表示C并作为解码器RNN的输入
优势：长度$n_{x}$和$n_{y}$可以不同
劣势：编码器RNN输出的上下文C维度过小而难以恰当地概括一个长序列
改进：让C为可变长度序列；将序列C的元素与输出序列元素相关联的注意力机制(attention mechanism)
深度循环网络
多数RNN可分解为：
- 从输入到隐藏状态
- 从隐藏状态到隐藏状态
- 从隐藏状态到输出
浅变换：通过深度MLP内单个层表示的变换，通常为由仿射变换和一个固定非线性表示组成的变化
深度RNN将RNN的状态分为多层有显著好处
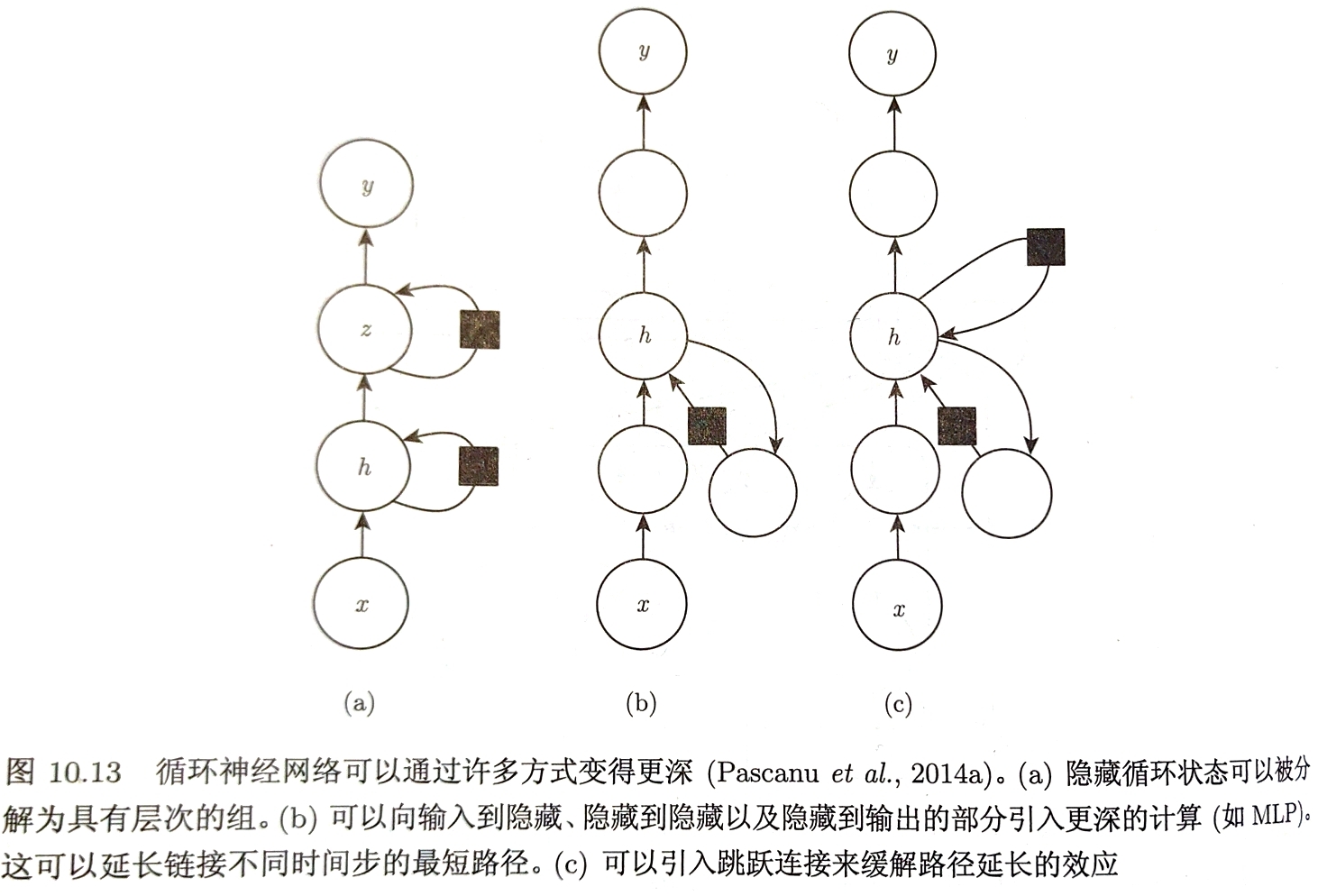a. 较低层将原始输入转化为对更高层的隐藏状态更合适表示的作用
b. 更进一步地在RNN三个块中各使用一个单独的MLP（可能深度的)
c. 增加深度可能会因优化困难损害学习效果，引入跳跃连接可以缓解这一问题
递归神经网络
构造深的树状结构而非RNN的链状结构 潜在用途：学习推论 优势：对于具有相同长度$\tau$的序列，深度可以急剧地从$\tau$减小为$O(log\tau)$ 问题：不知道如何是最佳的方式构造树 一种选择是不依赖数据的树结构，如NLP中句子语法分析树
|  |
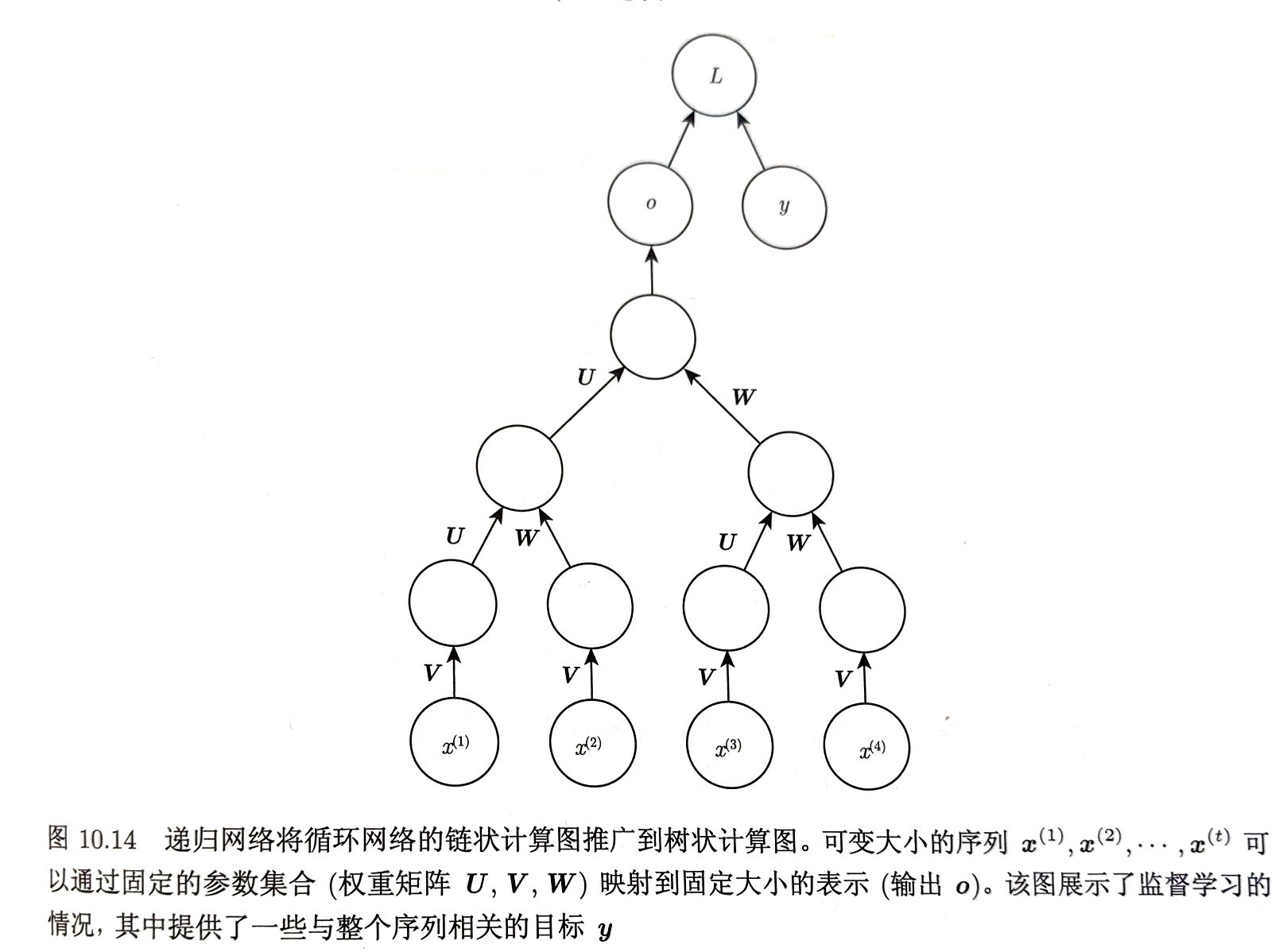长期依赖挑战
结果多阶段传播后的梯度倾向于消失（多数）或爆炸
循环网络涉及相同函数的多次组合，可能导致极端非线性行为
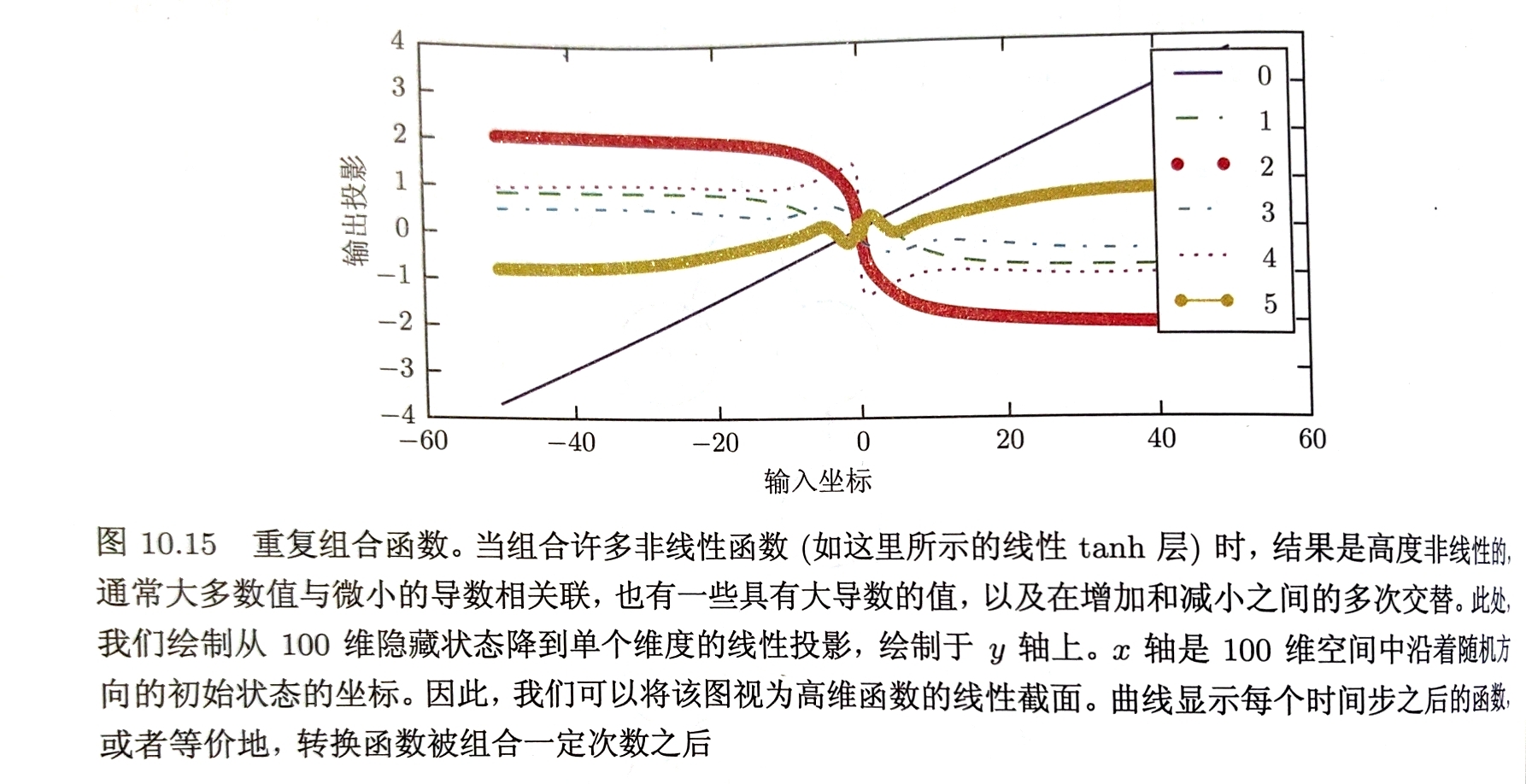
RNN使用的函数可以任认为$h^{t}=W^{\top}h^{t-1}$ 可简化为$h^{0}=(W^{t})^{\top}h^{0}$ 当$W$符合特征分解$W=Q\Lambda Q^{\top}$其中$Q$正交 循环性进一步简化为$h^{t}=Q^{\top}\Lambda^{t}Qh^{0}$ 特征值提升到t次后，导致幅值不到1的特征值衰减到0，大于1的激增，任何不与最大特征向量对齐的$h^{0}$部分被丢弃
非常深的前馈网络通过使用不同权重$w^{t}$而非循环网络，可经精心设计的比例避免梯度消失或爆炸问题
每当模型能够表示长期依赖，长期相互作用的梯度幅值会变得指数小，学习过程将非常长
回声状态网络ESN
RNN中隐藏层间循环权重映射和输入权重映射学习困难
回声状态网络(ESN)及流体状态机通过设定循环隐藏单元，使其能很好地捕捉过去输入历史并且只学习输出权重
流体状态机是采用脉冲神经元（二值输出）的ESN ESN和流体状态机由于隐藏单元形成了可能捕获输入历史不同方面的临时特征值，被称为储层计算
理念：将任意长度的序列映射为一个长度固定的向量(循环状态$h^{t}$)，之后施加一个线性预测算子以解决感兴趣问题 训练准则很容易设计为输出权重的凸函数 方法：储层计算将RNN视为动态系统并设定让动态系统接近稳定边缘的输入和循环权重
早期方法：使状态到状态转移函数的Jacobian矩阵特征值接近1 RNN的一个重要特征：Jacobian矩阵的特征值谱$J^{t}= \frac{\partial s^{t}}{\partial s^{t-1}}$ $J^{t}$谱半径为特征值最大绝对值
近期推荐：回声状态网络使用远大于1的谱半径，因为非线性的导数在许多时间步后接近0，有助于防止因过大谱半径导致的爆炸，推荐设置1.2的初始谱半径
渗透单元与多时间尺度策略
处理长期依赖的一种方法：设计工作在多个时间尺度的模型，使模型的某些部分在细粒度时间尺度上操作并能处理小细节，其他部分在粗粒度尺度上操作并能把遥远过去的信息有效传递
- 时间维度的跳跃连接：延迟循环网络
- 渗透单元： 通过设置线性自连接单元，并令这些连接的权重接近1获得导数乘积接近1 对某些$v$值应用更新$\mu^{t}\leftarrow \alpha\mu^{t-1}+(1-\alpha)v^{t}$积累一个滑动平均值$\mu^{t}$，当$\alpha$接近1时滑动平均值能记住过去很长时间信息 线性自连接的隐藏单元【渗透单元】模拟滑动平均行为 d时间步的跳跃连接可以确保单元总能被d个时间步前的值影响
- 多个时间尺度组织RNN状态：主动删除长度为1的连接并用更长的连接替代
门控RNN：长短期记忆LSTM及其他
门控RNN：长期短期记忆（LSTM）、基于门控循环单元的网络
类似渗漏单元，门控RNN基于生成通过时间的路径，其中导数既不消失也不爆炸 渗漏单元通过手动选择权重，门控RNN推广为每个时间步都可能改变的连接权重 门控RNN令神经网络学会决定何时清除状态（遗忘）
LSTM
通过自循环产生梯度长时间持续流动的路径
LSTM使自循环的权重视上下文而定
门控此自循环（由另一个隐藏单元控制）的权重，积累的时间尺度可以动态地改变
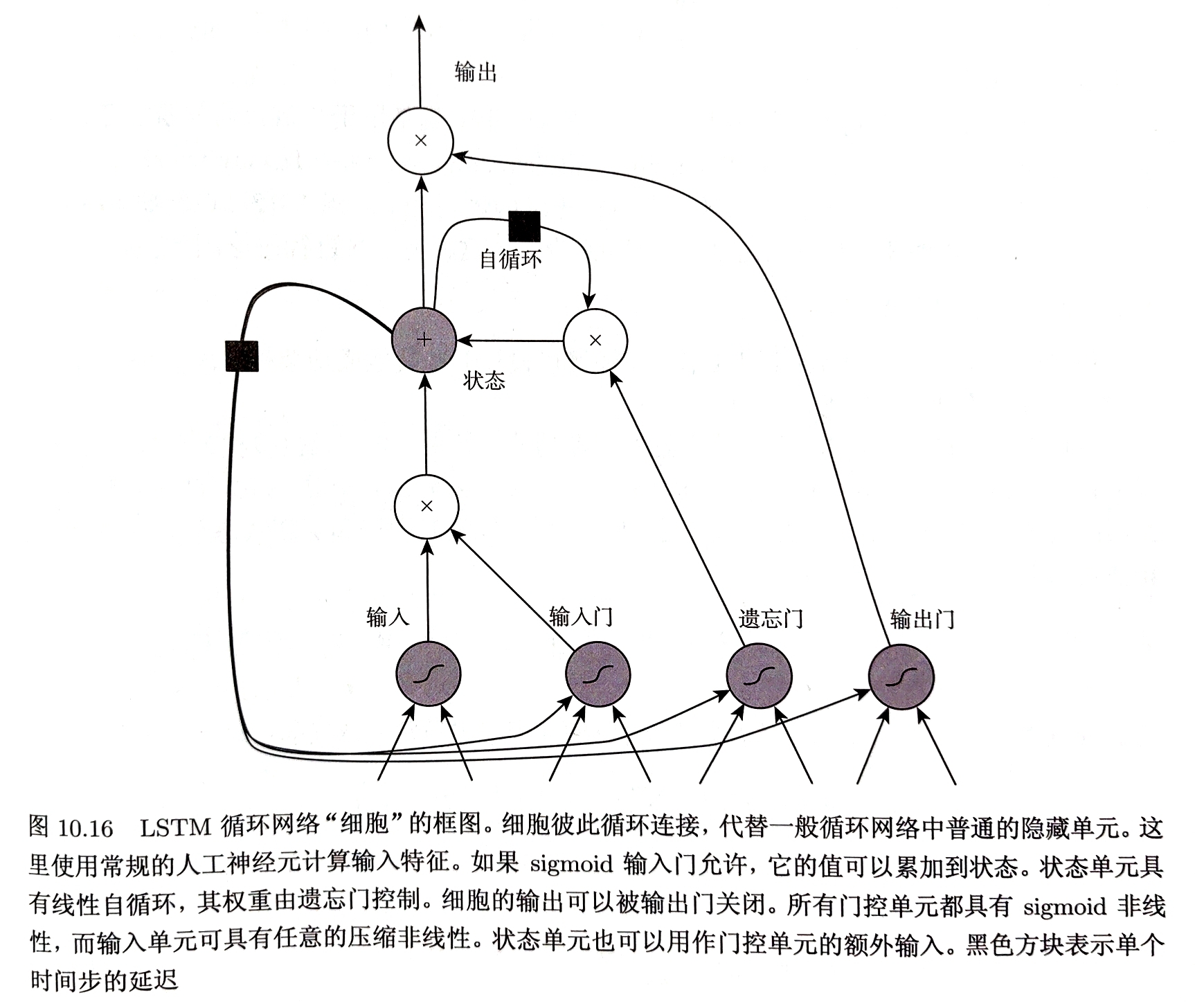状态单元$s_{i}^{t}$自环的权重由遗忘门$f_{i}^{t}$控制，由sigmoid单元将权重设置为0和1之间
$f_{i}^{t}=\sigma(b_{i}^{f}+\sum\limits_{j}U_{i,j}^{f}x_{j}^{t}+\sum\limits_{j}W_{i,j}^{f}h_{j}^{t-1})$
$x^{t}$当前输入向量；$h^{t}$当前隐藏层向量，包含所有LSTM细胞的输出
$b^{f},U^{f},W^{f}$为偏置、输入权重、遗忘门循环权重
LSTM细胞内部状态更新：$s_{i}^{t}=f_{i}^{t}s_{i}^{t-1}+g_{i}^{t}\sigma(b_{i}+\sum\limits_{j}U_{i,j}x_{j}^{t}+\sum\limits_{j}W_{i,j}h_{j}^{t-1})$
$f_{i}^{t}$自环权重；$b,U,W$ LSTM细胞中偏置、输入权重、循环权重
外部输入门单元$g_{i}^{t}=\sigma(b_{i}^{g}+\sum\limits_{j}U_{i,j}^{g}x_{j}^{t}+\sum\limits_{j}W_{i,j}^{g}h_{j}^{t-1})$
输出$h_{i}^{t}=tanh(s_{i}^{t})q_{i}^{t}$
输出门$q_{i}^{t}=\sigma(b_{i}^{o}+\sum\limits_{j}U^{o}{i,j}x{j}^{t}+\sum\limits_{j}W^{o}{i,j}h{j}^{t-1})$
$b^{o},U^{o},W^{o}$为偏置、输入权重、循环权重
门控循环单元GRU
单个门控单元同时控制遗忘因子和更新状态单元的决定
$h_{i}^{t}=u_{i}^{t-1}h_{i}^{t-1}+(1-u_{i}^{t-1})\sigma(b_{i}+\sum\limits_{j}U_{i,j}x_{j}^{t}+\sum\limits_{j}W_{i,j}r_{j}^{t-1}h_{j}^{t-1})$
$u_{i}^{t}=\sigma(b_{i}^{u}+\sum\limits_{j}U_{i,j}^{u}x_{j}^{t}+\sum\limits_{j}W_{i,j}^{u}h_{j}^{t-1})$更新门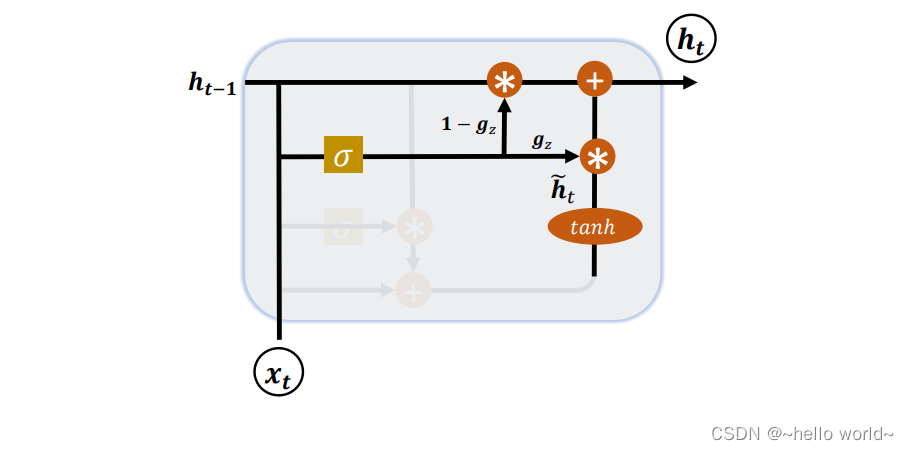
$r_{i}^{t}=\sigma(b_{i}^{r}+\sum\limits_{j}U_{i,j}^{r}x_{j}^{t}+\sum\limits_{j}W_{i,j}^{r}h_{j}^{t-1})$复位门
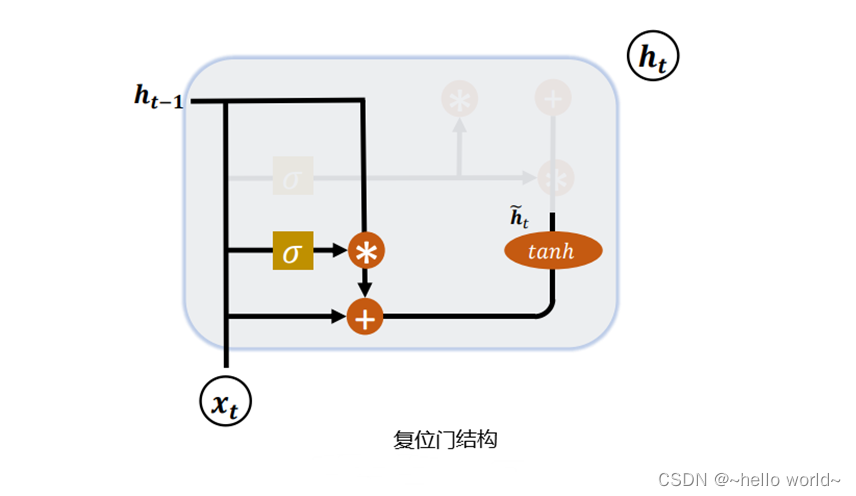
复位和更新门能独立地忽略状态向量的一部分 更新门像条件渗漏积累器一样可以线性门控任意维度，从而选择将它复制或完全替换