第11章 实践方法论
实践设计流程:
- 确定目标(依据问题决策)
- 误差度量方法
- 目标值
- 建立端到端的工作流程
- 估计合适的性能度量
- 搭建系统
- 确定性能瓶颈
- 检查未及预期环节
- 过拟合&欠拟合
- 数据缺陷
- 软件缺陷
- 反复改进
- 增加数据
- 调整超参数
- 改进算法
性能度量
精度、召回率 PR曲线 F分数
默认的基准模型
一般项目开始时可以从简单的统计模型开始
对象识别、语音识别、机器翻译等开始于一个合适的深度学习模型 根据数据的结构选择一类合适的模型
- 固定大小的向量输入的监督学习:全连接的前馈网络
- 输入已知的拓扑结构(如图像):卷积网络
- 分段线性单元亦可(ReLU、 Leaky ReLU、PReLu、maxout)
- 序列数据:门控循环网络(LSTM、GRU)
优化算法:
- 具有衰减学习率以及动量的SGD
- 流行的衰减算法:线性衰减、指数衰减、每次发生验证错误停滞时将学习率降低2~10倍
- Adam算法
- 批标准化在最初的基准中忽略;当优化出现问题时立即使用批标准化
正则化:
- 除非极大训练集,最初应包含一些温和的正则化
- 提前终止被普遍采取
- Dropout
-
使用批标准化时可省略Dropout
- 若任务和其他被广泛研究的任务相似,基模型应复制先前研究中已知性能良好的模型和算法;甚至复制一个训练好的模型
无监督学习
- NLP能大大受益于无监督学习
- CV除非在半监督设定下,无监督没有益处
- 若应用环境中无监督学习很重要则将其包含在第一个端到端的基准中
- 否则只有解决无监督问题时才会第一次尝试无监督学习
- 发现初始基模型过拟合时可尝试加入无监督模型
是否收集更多数据
收集更多数据往往比改进算法更有效 判断标准
- 训练集性能
- 模型在训练集上很差,更换算法
- 性能可接受
- 增加网络层或每层增加更多的隐藏单元
- 调整学习率等超参数的措施改进学习算法
- 更大规模模型和优化效果不佳
- 问题源自训练数据的质量
- 收集更干净或特征更丰富的数据
- 测试集性能
- 测试集性能差
- 收集更多数据
- 降低模型大小或改进正则化
- 依据训练集规模和泛化误差之间的关系预测需要数据量
- 测试集性能差
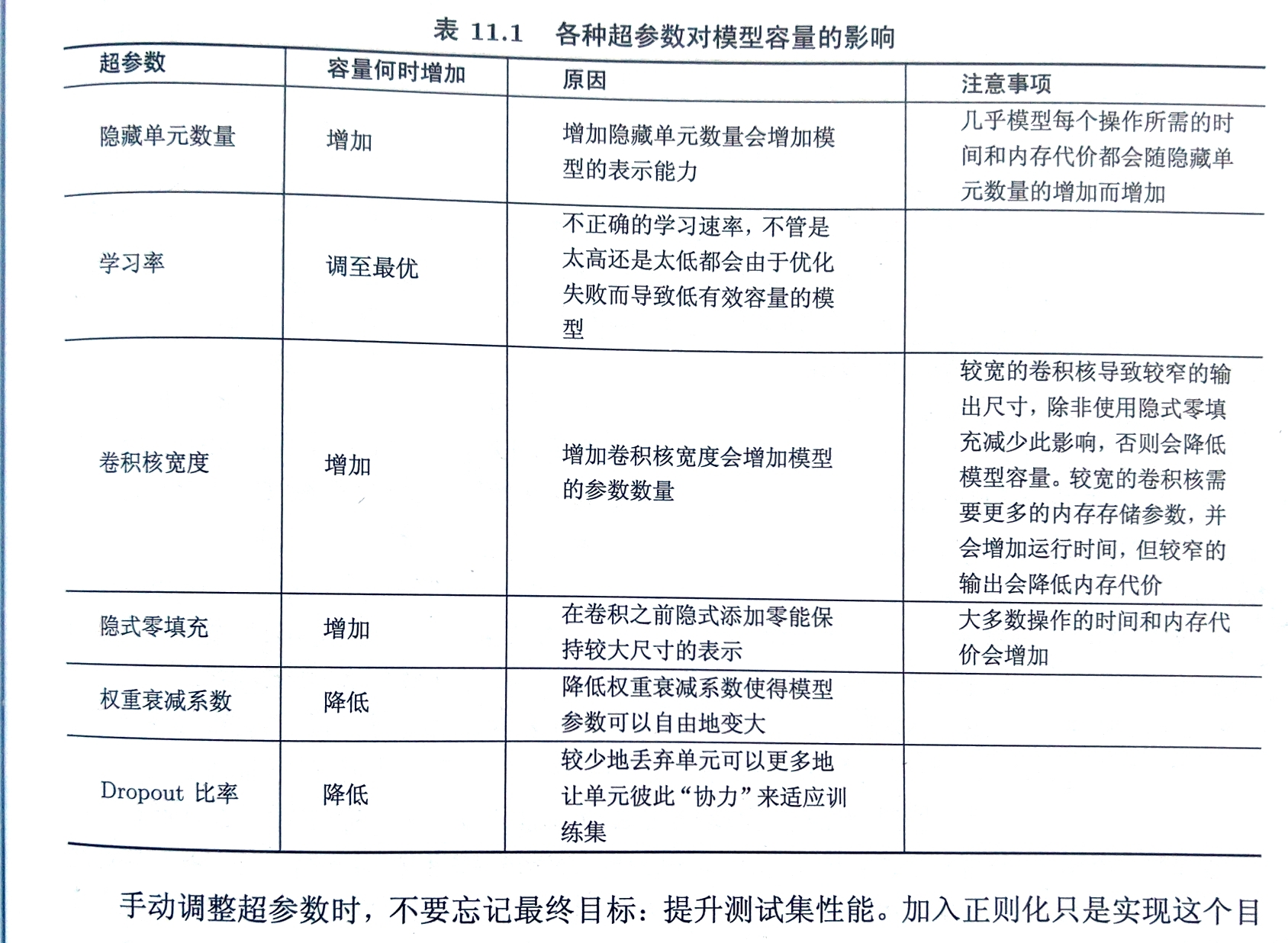
超参数选择
手动调参
主要目标是调整模型的有效容量以匹配任务的复杂度 有效容量受限于3个因素:
- 模型的表示容量
- 学习算法成功最小化代价函数的能力
- 代价函数和正则化模型的程度
学习率是最重要的超参数 若仅有时间调整一个超参数就调整学习率
其他超参数调整应同时监测训练误差和测试误差
若训练集误差大于目标错误率,需增加模型容量改进模型
若没有正则化且确信优化算法正确运行,应添加更多的网络层或隐藏单元
若测试集误差大于目标错误率,且训练集误差较小则通过正则等减少模型容量
自动超参数优化算法
网格搜索grid search
有3个或更少的超参数时常用网格搜索 对每个超参数选择一个较小的有限值集,通过多个超参数有限值集笛卡尔乘积获取备选网格 有序数值:最小和最大元素可以基于先前相似实验的经验保守挑选;通常在对数尺度挑选合适的值 通常重复进行网格搜索并依靠选择结果调整备选集区间 缺点:计算代价岁超参数数量呈指数级增长
随机搜索
为每个超参数定义一个边缘分布:
- Bernouli分布
- 对数尺度上的均匀分布
例:$log_learning_rate\sim u(-1,-5),learning_rate=10^{log_learning_rate}$ 随机搜索能够更快地减小验证集误差
随机搜索通常也多次进行
基于模型的超参数优化
大部分基于模型的超参数搜索算法都使用贝叶斯回归模型估计每个超参数的经验集误差期望和期望的不确定性
前沿方法:Spearmint、TPE、SMAC
调试
可视化计算中模型的行为 可视化最严重的错误 根据训练和测试误差检测 拟合极小的数据集检验软件问题
比较反向传播导数和数值导数
- 比较自动求导的实现和通过有限差分计算导数
- 导数定义$f’(x)=\mathop{\lim}\limits_{\epsilon\rightarrow 0} \frac{f(x+\epsilon)-f(x)}{\epsilon}$
- 近似导数$f’(x)\approx\frac{f(x+\epsilon)-f(x)}{\epsilon}$
- 使用中心差分提高近似准确率$f’(x)\approx\frac{f(x+ \frac{1}{2}\epsilon)-f(x- \frac{1}{2}\epsilon)}{\epsilon}$
- $\epsilon$是小的但不会由于数值计算精度问题产生舍入误差
监督激活函数值和梯度的直方图