第12章 应用
大规模深度学习
计算机视觉
预处理
图像应该被标准化 许多CV架构需要标准尺寸的图像，必须剪裁或缩放图像以适应该尺寸；一些卷积模型接受可变大小输入
对比度归一化 在许多任务中，对比度是能够安全移除的最为明显的变化源之一 对比度：图像中亮像素和暗像素之间差异的大小 图像三维张量对比度：$\sqrt{\frac{1}{3rc}\sum\limits_{i=1}^{r}\sum\limits_{j=1}^{c}\sum\limits_{k=1}^{3}(\mathsf{X}{i,j,k}-\bar{\mathbf{X}})^{2}}$ 其中$\bar{\mathbf{X}}=\frac{1}{3rc}\sum\limits{i=1}^{r}\sum\limits_{j=1}^{c}\sum\limits_{k=1}^{3}\mathsf{X}_{i,j,k}$
全局对比度归一化GCN
旨在通过从每个图像中减去其平均值，然后重新缩放使其像素上的标准差等于某个常数$s$防止图像具有变化的对比度
给定输入图像$\mathbf{X}$全局对比度归一化输出图像$\mathbf{X}^{‘}$
$\mathsf{X}^{‘}{i,j,k}=s \frac{\mathsf{X}{i,j,k}-\bar{\mathsf{X}}}{max{\epsilon, \sqrt{\lambda+ \frac{1}{3rc}\sum\limits_{i=1}^{r}\sum\limits_{j=1}^{c}\sum\limits_{k=1}^{3}(\mathsf{X}_{i,j,k}-\bar{\mathsf{X}})^{2}}}}$
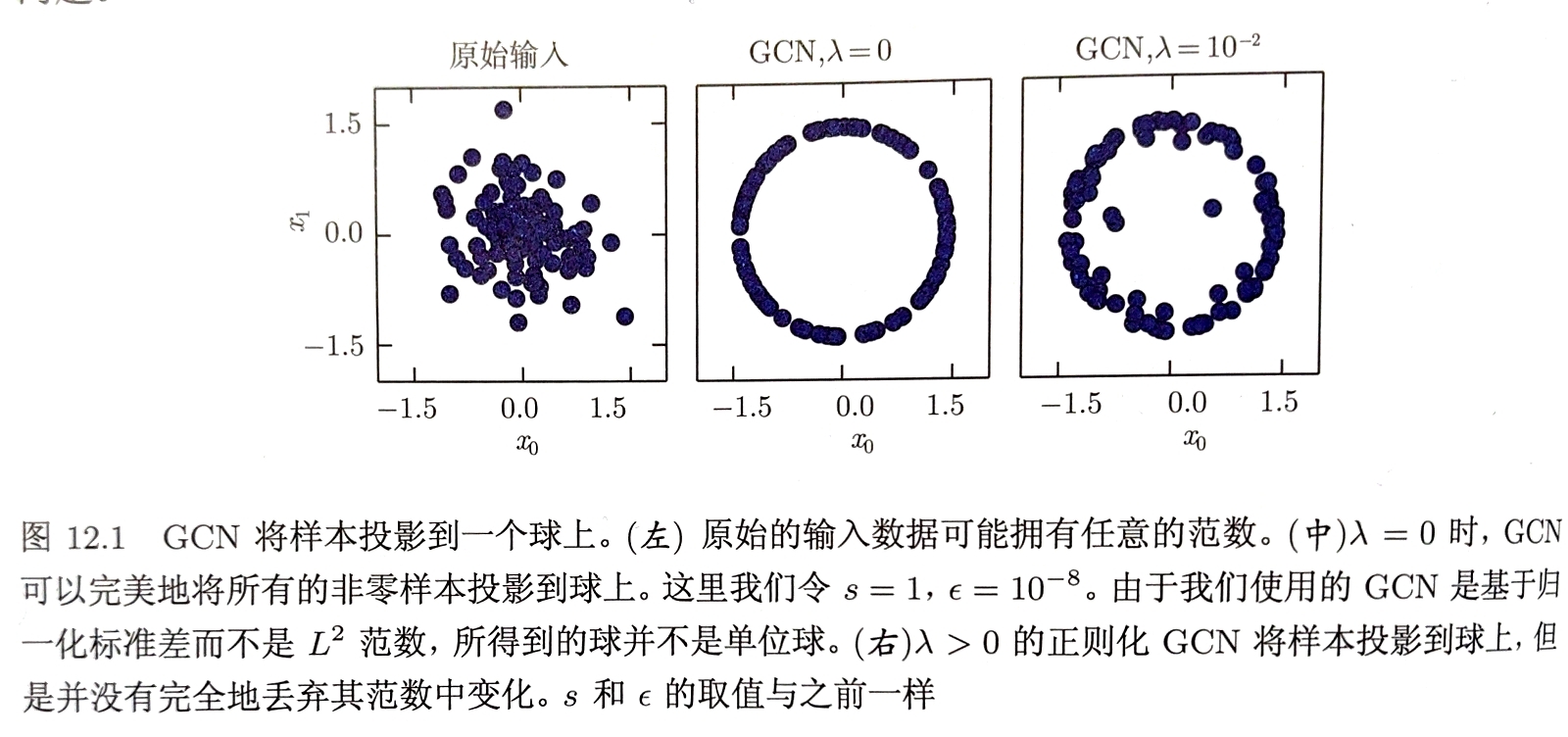
局部对比度归一化LCN
确保对比度在每个小窗口上被归一化，不是作为整体在图像上被归一化
在所有情况下，可以通过减去邻近像素的平均值并除以邻近像素的标准差来修改像素
数据集增强
某些情况下输入的翻转可以增强数据集 图像颜色的随机扰动 输入的非线性几何变形
语音识别
令$\mathbf{X}=(x^{1},x^{2},…,x^{T})$表示语音的输入向量（传统做法以20ms为一帧分割信号） 某些深度学习系统直接从原始输入中学习特征 令$\mathbf{y}=(y_{1},y^{2},…,y_{N})$表示目标的输出序列
自动语言识别ASR任务是构造一个函数$f^{}_{ASR}$使给定声学序列$\mathbf{X}$的情况下计算可能的语言序列$\mathbf{y}$ $f^{}{ASR}(\mathbf{X})=\mathop{\arg\max}\limits{y}P^{}(y|\mathbf{X}=\mathbf{X})$ 其中$P^{}$是给定输入值$\mathbf{X}$时对应目标$y$的真实条件分布
早年常用隐马尔可夫模型与高斯混合模型结合的GMM-HMM模型 GMM对声学特征和因素之间的关系建模，HMM对音素序列建模 如今使用神经网络
自然语言处理
多数情况下将自然语言视为一系列词
n-gram
语言模型定义了自然语言中标记序列的概率分布 最早成功的语言模型基于固定长度序列的标记模型n-gram n-gram定义了条件概率：给定前n-1个标记后的第n个标记的条件概率 $P(x_{1}, …,x_{r})=P(x_{1},…,x_{n-1})\mathop{\prod}\limits_{t=n}^{\tau}P(x_{t}|x_{t-n+1},…,x_{t-1})$ $n=3$三元语法 通常同时训练n-gram模型和(n-1)-gram模型以便于计算概率 $P(x_{t}|x_{t-n+1},…,x_{t-1})= \frac{P_{n}(x_{t-n+1},…,x_{t})}{P_{n-1}(x_{t-n+1},…,x_{t-1})}$
缺陷：许多情况下从训练集技术估计得到的$p_{n}$很可能为0；容易引起维度灾难 改进：多数采用平滑技术；另一种流行措施是包含高阶和低阶n-gram模型的混合模型
神经语言模型HLM
用来克服维度灾难的语言模型 使用词的分布式表示对自然语言序列建模 神经语言模型能够识别两个相似的词，并且不丧失将每个词编码为彼此不同的能力 模型共享一个词（及其上下文）和其他类似词的统计强度 通过将每个训练句子与指数数量类似句子相关联客服问题
词嵌入：把词表大小的高维空间嵌入到低维空间中
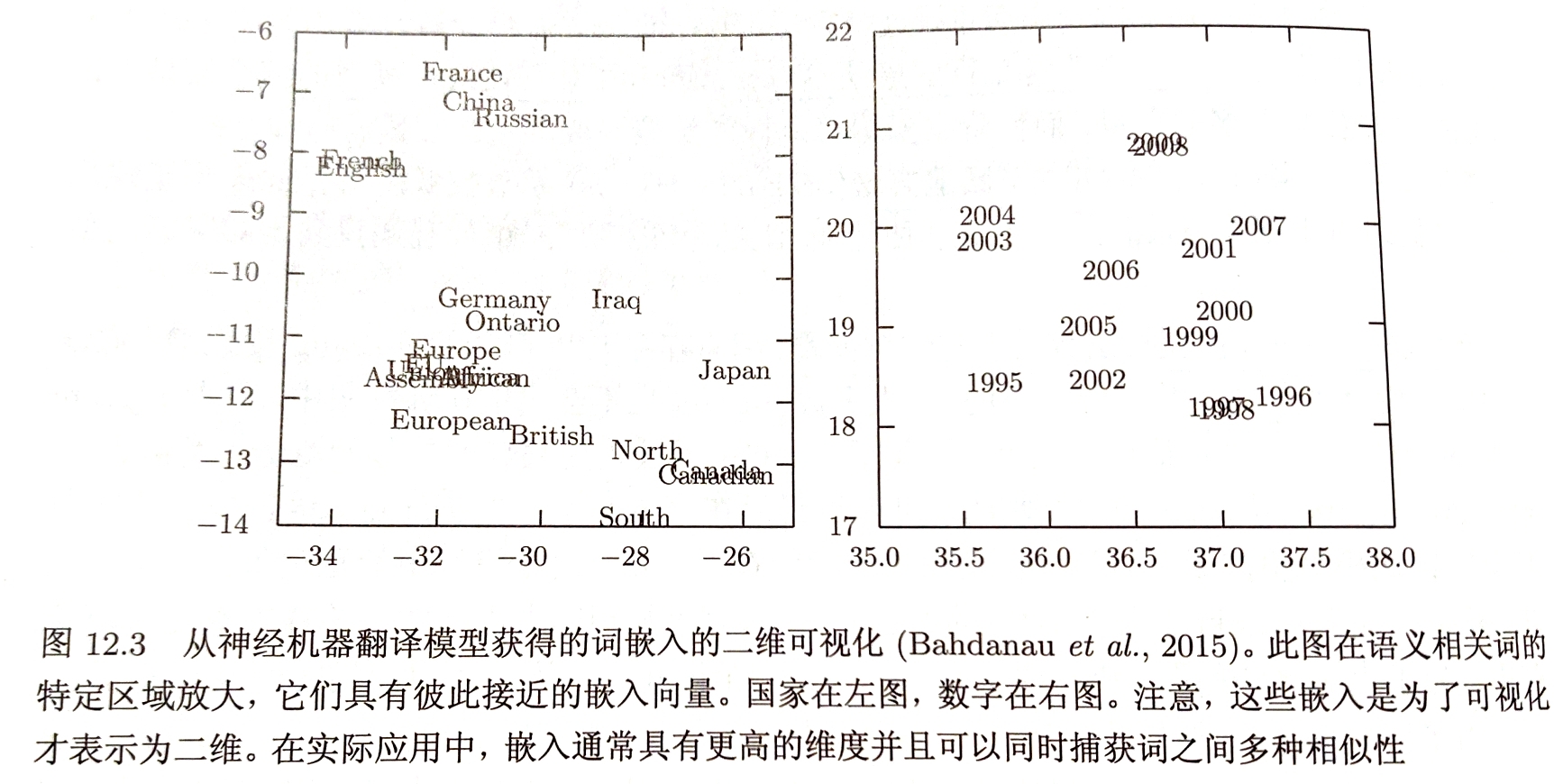
高维输出 输出词句而非字符
使用大词汇表 假设$h$是用于预测输出概率$\hat{h}$的顶部隐藏层 仿射softmax输出层：$a_{i}=b_{i}+\sum\limits_{j}W_{ij}h_{j}\quad \forall i\in{1,…,|\mathbb{V}|}$ $\hat{y}{i}= \frac{e^{a{i}}}{\sum\limits_{i’=1}^{|\mathbb{V}|}e^{a_{i’}}}$ 缺点：操作复杂度极高
-
改进方案1：使用短列表 将词汇表$\mathbb{V}$分为最常见词汇的短列表$\mathbb{L}$（由神经网络处理）和稀有词汇的尾列表$\mathbb{T}=\mathbb{V}\setminus\mathbb{L}$(由n-gram处理) 神经网络需额外添加sigmoid输出单元估计$P(i\in \mathbb{T}|C)$预测上下文C之后出现的词位于尾列表的概率 缺点：潜在泛化优势仅限于常用词
-
改进方案2：分层softmax 减少大词汇表高维输出层计算负担的经典方法为 分层地分解概率 $|\mathbb{V}|$因子可以降低到$log|\mathbb{V}|$维度 通过将因子分解引入神经语言模型构建层次结构 嵌套类别构成平衡树，叶子为词，树的深度为$log|\mathbb{V}|$ 选择一个词的概率由路径上的每个节点通向该词分枝概率的乘积 预测每个节点所需的条件概率使用逻辑回归模型并为模型提供与输入相同的上下文C 通常使用标准交叉熵损失，最大化正确判断序列的对数似然
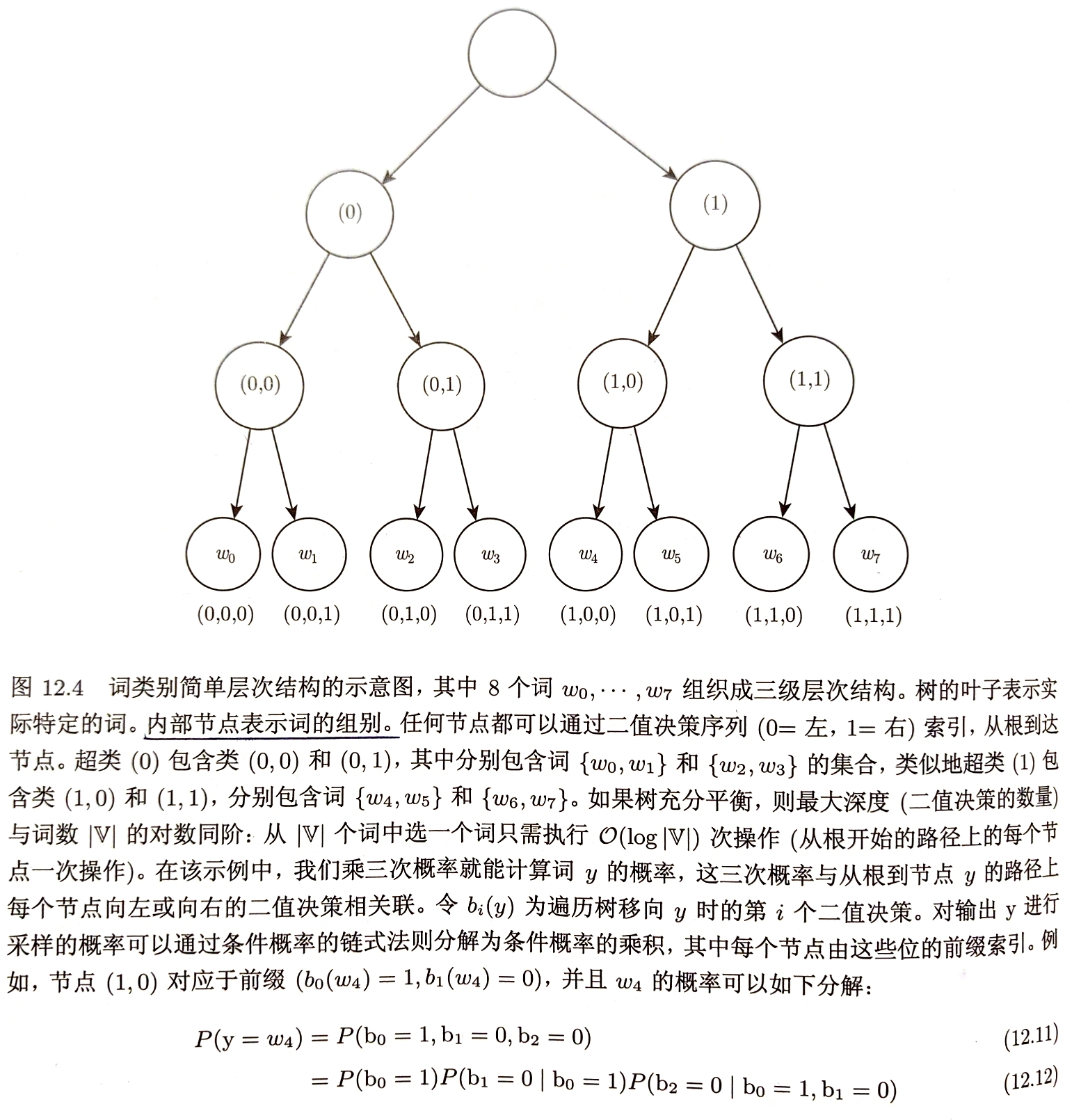缺点：实践中分层softmax倾向于更差的测试结果
重要采样 避免明确计算所有未出现在下一位置的词对梯度的贡献 梯度：$\frac{\partial log\ P(y|c)}{\partial \theta}= \frac{\partial log\ softmax_{y}(a)}{\partial \theta}= \frac{\partial}{\partial \theta}log\ \frac{e^{a_{y}}}{\sum\limits_{i}e^{a_{i}}}= \frac{\partial a_{y}}{\partial \theta}-\sum\limits_{i}P(y=i|C) \frac{\partial a_{i}}{\partial \theta}$ 其中$a$是presoftmax激活向量，每个词对应一个元素 第一项为正相项，第二项为加权的负相项 负相项是期望值，可以采用蒙特卡洛采样估计，但要规避从模型本身采样 可以从提议分布q，并通过适当权重校正从错误分布采样中引入偏差——重要采样 为规避从模型中采样，将重要性权重归一化加和为1——有偏重要采样 对负词$n_{i}$进行采样，相关联的梯度被加权$w_{i}= \frac{p_{n_{i}}/q_{n_{i}}}{\sum\limits_{j=1}^{N}p_{n_{j}}/q_{n_{j}}}$ 对来自q的m个负样本形成负相估计对梯度的贡献： $\sum\limits_{i=1}^{|\mathbb{V}|}P(i|C) \frac{\partial a_{i}}{\partial \theta}\approx \frac{1}{m}\sum\limits_{i=1}^{m}w_{i} \frac{\partial a_{n_{i}}}{\partial \theta}$
集成n-gram和神经语言模型
现代注意力机制本质上是加权平均
推荐系统
协同过滤类算法
- 非参数方法
- 最近邻等
- 参数方法
- 依赖于为每个用户和每个项目学习分布式表示（嵌入）
- 目标变量的双线性预测（评级等）是成功简便方法
- $\hat{R}$预测矩阵
- $A$矩阵行中是用户嵌入；$B$矩阵列中具有项目嵌入
- $b、c$针对每个用户（用户平常坏脾气或积极程度）、项目（大体受欢迎程度）的偏置
- $\hat{R}{u,i}=b{u}+c_{i}+\sum\limits_{j}A_{u,j}B_{j,i}$
- 通常希望最小化预测评级$\hat{R}{u,i}$和实际评级$R{u,i}$间平方误差
- 缺陷：新用户无法评估——冷启动推荐问题
- 改进：引入单个用户和项目的额外信息-基于内容的推荐系统
使用推荐系统收集数据时，得到的是有偏且不完整的用户偏好观：只能看到用户对推荐给他们项目的反应；无法获得未向其进行推荐的用户的任何信息
强化学习需要权衡探索和利用