本周阅读摘选 2023-02-06 → 2023-02-12 目录

• 学术相关
  • AI绘画爆火背后：扩散模型原理及实现
  • 引入因果线索的对话情绪识别模型CauAIN
    • 因果线索获取
    • 因果意识交互
    • 实验结果
    • 消融实验
  • 从玄学走向科学：AB测试驱动的科学增长
  • 广告场景下双边市场的实验设计
  • 基于话题标签（#）的社交媒体事件流行预测
    • 文献综述
    • 解决方案架构
    • 高影响力话题标签筛选
    • 高影响力话题标签级联模型
    • XGBOOST模型流行度预测
    • 动态预测模型维护
    • 实验估计
  • 美丽遇见德鲁克（十二）：拯救被侮辱与被损害的营销
• 业界动态
  • InfoQ：中国软件技术发展洞察和趋势预测报告2023
  • 36氪研究院丨2023年中国自动驾驶行业研究报告
• 技术技巧
  • R包：modelsummary多模型做表导出
  • R包：ggstats辅助ggplot2对统计量作图
• 娱乐
  • 外星生命或智能摆在面前，你能认出来吗？——“梯径”提供的思路

学术相关

AI绘画爆火背后：扩散模型原理及实现

​ 只对大致原理做简单了解，短期来看，我认为我在MKT领域的研究至多涉及到它的应用。

​ DDPM模型（Denoising Diffusion Probabilistic Model)算是现阶段diffusion模型的开山鼻祖。区分于前人的GAN、VAR和flow等模型，diffusion模型的整体思路是通过一种偏向于优化的方式，逐步从一个纯噪声图片中生成图像。

去噪

​ 第一步需要减少数字图像中因数字化、传输过程中受设备和外部环境等因素干扰出现的噪声，获取干净图像。但实践中，去噪非常复杂，因此有人反其道而行之，先通过加噪的方式将图像变成纯噪声图像，再把这一过程反向运行。所以diffusion模型的训练-推理流程为：前向过程逐步加噪，将图片转换为一个近似高斯分布的纯噪音图像；再采用反向过程逐步去噪，生成图像；最后以增大原始图像和生成图像的相似度作为目标，优化模型。

前向过程/扩散过程（forward/diffusion process）

​ 一个参数化的马尔科夫链。从初始数据分布出发，每步在数据分布中添加高斯噪声，持续T次。其中从第t-1步到第t步的过程使用高斯分布处理：$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-\beta_t}x_t,\beta_t I)$

​ 随着t不断增大，原始数据逐渐失去特征，最终获得纯噪声图像。在扩散过程中，每一步都可以通过超参数控制。在我们知晓原始图片的前提下，扩散过程是已知且可控的。此外，由于高斯分布可加性该过程可以一步到位：$q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{\bar{\alpha}_t}x_0,(1-\bar{\alpha}_t)I)$，其中$\sqrt{\bar{\alpha}_t}$和$(1-\bar{\alpha}_t)$为组合系数，本质上是超参数。

反向过程（reverse process）

​ 反向过程也是马尔科夫链，但其中的参数需要机器学习确定，通过样本近似估计分布$p_\theta(x_{t-1}|x_t)$。

目标函数

​ 度量生产图像和真实图像的相近程度有效考虑交叉熵函数，但是由于交叉熵的真实后验分布通常难以计算，所以采用ELBO证据下界变分推断替代，用函数近似真实后验分布。

大模型平台

​ MindSpore提供了开发完备的DDPM模型。华为诺亚团队和中软分布式并行实验室、昇腾计算产品部联合开发了基于扩散模型的中文文生图模型——悟空画画。

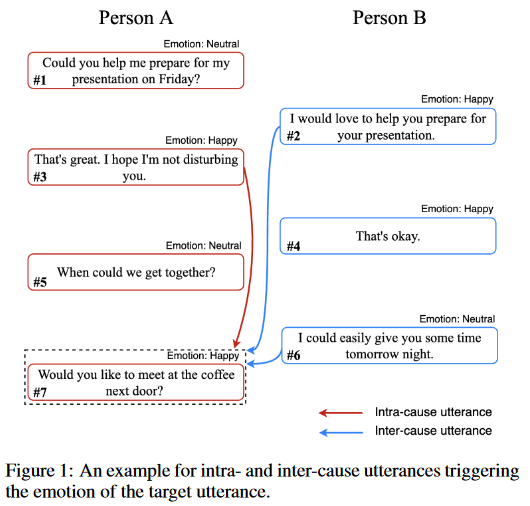
引入因果线索的对话情绪识别模型CauAIN¹

​ 对话情绪识别(ERC)旨在预测对话中每条对话语句的情感，其关键挑战是如何捕获对话中的情感变化动态(Emotional Dynamics)，即不同对话者之间的情感交互。这篇论文通过建立具有将当前目标语句及导致其情绪原因语句进行关联能力的模型。

​ 这篇文章将导致目标语句情绪的关联语句分为自因语句（由同一讲述人先前情感继承的语句）和互因语句（由对话者语句影响情感的语句）。模型的目标是识别语句的对话情绪，即对有$N$个连续语句集合${u_1,u_2,…,u_N}$和$M$个对话者${s_1, s_2,…,s_M}$数据，预测对话者$s_i$的语句$u_j$的情感标签$e_k$。

​ 该模型整体包含三个部分：因果线索获取、因果线索检索、因果话语回溯和情感识别。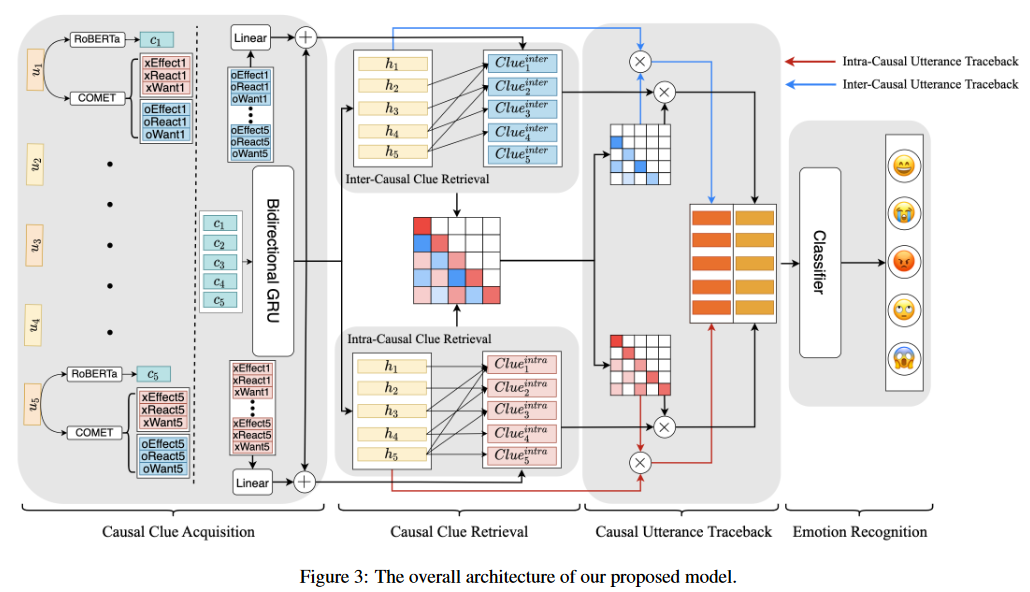

因果线索获取

​ 本文采用ATOMIC数据集进行因果线索获取。前人工作²表明神经网络能够在ATOMIC丰富的推理知识帮助下，对未曾见过的事件可能的原因和效果进行预测。本研究借助该数据集分析对话语境，构建常识Transformer模型COMET，基于因果关系探索六种关系类型，其中$xReact,xEffect, xWant$作为内因线索，$oReact, oEffect, oWant$作为互因线索。通过将对话中的每句话和不同关系类型组合依次输入COMET模型，将最后一个编码层的隐藏状态作为需要的因果线索。之后对于每个语句$u_i$将三种自身原因关系类型的线索拼接起来，并通过线性层得到$2d_h$维的结果$Clue_i^{intra}$；同理获得互因线索$Clue_i^{inter}\in R^{2d_h}$。

• 话语级别表示

​ 通过广泛应用的预训练模型RoBERTa提取话语级别特征向量。对每一句话语$u_i={w_1, w_2,…,w_L}$，添加起始标记$|CLS|$，以${|CLS|,w_1,w_2,…,w_L}$的形式喂给RoBERTa对话语级别情感分类任务进行微调。微调完成后，再将${|CLS|,w_1,w_2,…,w_L}$输入RoBERTa模型获取特征向量$c_i=RoBERTa(|CLS|,w_1,w_2,…,w_L)$，$c_i\in \mathbb{R}^{d_m}$，其中$d_m$为RoBERTa中隐藏层词元的维度，最后四层的均值作为每句话语的话语级别特征向量。

• 对话级别表示

​ 基于话语级别特征$c_i$，应用双向门控循环单元GRU对毗邻话语的顺序依赖关系进行建模。对话$h_i$表示为$h_i=\overleftrightarrow{GRU}(c_i,h_{i-1})$，$h_i\in\mathbb{R}^{2d_h}$，其中$d_h$表示门控循环单元的输出维度。

因果意识交互

​ 为了从对话中获取丰富的动态情感线索及清晰的自因语句和互因语句的依赖关系，作者设计了两阶段的因果意识交互——因果线索检索和因果话语回溯。

因果线索检索

​ 通过检索自因话语和互因话语，为它们配置识别情感因果的权重。其中自因话语的检索得分为$scores_{i,j}^{intra}=\frac{[f_q(h_i)(f_k(h_i)+f_e(Clue_j^{intra}))]mask_{i,j}^{intra}}{\sqrt{d_h}} $，里面$f_q(x),f_k(x),f_e(x)$是线性变换，$mask_{i,j}^{intra} $保证目标语句$h_i$检索的语句都是同一讲述人的内因线索，且符合时间顺序。

​ $mask_{i,j}^{intra}=\left\{\begin{aligned} &1,j\leq i\ and\ \phi(h_i)=\phi(h_j)\\ &0,else\end{aligned}\right.$，其中$\phi(x)$是把语句索引对应到讲述人的映射。互因语句的得分与之类似，$scores_{i,j}^{inter}=\frac{[f_q(h_i)(f_k(h_j)+f_e(Clue_j^{inter}))]mask_{i,j}^{inter}}{\sqrt{d_h}}$。之后通过Softmax函数获取两类语句的权重$\alpha_{i,j}^{joint}=softmax(scores_{i,j}^{intra}+scores_{i,j}^{inter})$。

作者没有对函数的设计进行解释，所以我只能简要猜测。首先，$Clue_j^{intra}$是基于ATOMIC常识因果推理数据集构建的COMET模型，对语句$j$进行三种内因关系推理并嵌入的内因线索。而$h_i$和$h_j$都是基于预训练模型RoBERTa提取的话语级别特征向量通过GRU构建的对话级别特征向量。所以公式本质上是寻找同一讲述人顺序语句之间的交互关系，其中后面的语句添加了因果线索信息，满足因果关系的时间序列性。我不知道得分除去$\sqrt{d_h}$维度这一常数的意义在哪里。

因果话语回溯

​ 本环节使模型通过不同的权重，更加注重话语相关性与情感线索的关系。将$\alpha^{joint}$分解为$\alpha^{intra}$和$\alpha^{inter}$两部分。因果意识上下文可以表示为$\tilde{h}_i=\sum\limits_{j\in S(i)}\alpha_{i,j}^{intra}f_q(h_j)+\sum\limits_{j\in O(i)}\alpha_{i,j}^{inter}f_q(h_j)$，其中$S(i)$是同一讲述人的话语集，$O(i)$是其他讲述人的话语集。因果线索中的情感信息也应该被考虑$\tilde{c}_i=\sum\limits_{j\in S(i)}[\alpha_{i,j}^{intra}(f_k(h_j)+f_e(Clue_j^{intra}))]+[\sum\limits_{j\in O(i) }\alpha_{i,j}^{inter}(f_k(h_j)+f_e(Clue_j^{inter})]$

​ 最终的因果意识表示$h_{i}^f=\tilde{h}_i\bigoplus \tilde{c}_i$。

情绪识别

​ 预测$\hat{y}=softmax(W_eh^f+b_e)$，采用交叉熵损失函数$L=-\frac{1}{N}\sum\limits_{i=1}^N\sum\limits_{j=1}^E\hat{y}_i^j\cdot log(y_i^j)$，其中$E$是表情类别。

实验结果

​ 数据集：IEMOCAP、DailyDialog、MELD

​ 基准模型：ICON、DialogueRNN、DialogueGCN、IEIN、RGAT、COSMIC、DialogXL、DialogueCRNN、SKAIG、KI-NET

​ 评价指标：F1，micro-F1，macro-F1

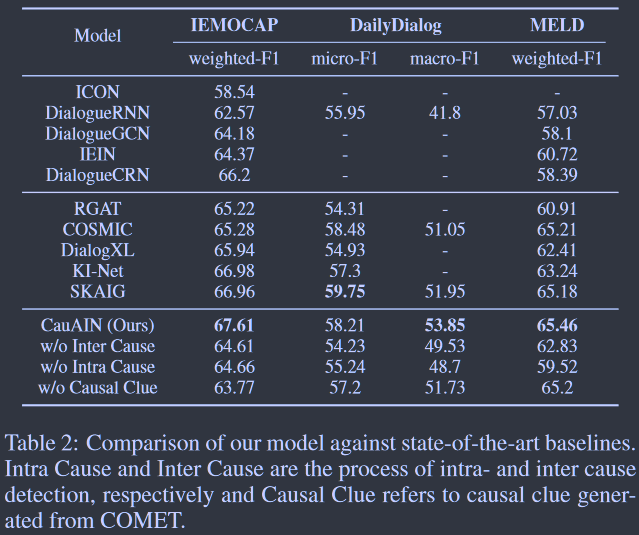
​ CauAIN在IEMOCAP、DailyDialog的 macro-F1上取得了更高的成绩，表明情感原因检测在具有丰富对话背景信息、对话长度较常且有丰富情感动态线索的数据集上表现良好，且能部分缓解数据不平衡的影响。作者认为由于MELD对话较短，所以CauAIN表现有限。

消融实验

情感因果作用

​ 作者分别移除了模型中与ATOMIC中学习到的内因因果、互因因果相关部分（TABLE 2倒数第2、3行），模型效果均有明显下降，说明内因和互因因果都在模型中起到重要作用。在MELD中，只有内因因果起到重要作用，互因因果作用很小（对话短）。

因果线索作用

​ 作者从IEMOCAP的测试集中随机抽取100段对话进行人工评估，同时比较由因果线索检索获取的$\alpha^{joint}$权重最高的3个语句视作情绪原因的候选集。实验中要求人类标注者判断原因语句是否归属于候选集，评价标准为准确率。结果表明，在因果线索的帮助下，模型的情绪原因回溯达到60%的准确率，而没有因果线索的识别准确率会降低到53%。

​ 最后，TABLE 2的最后一行显示了不使用COMET生成因果线索的结果。

作者没有讨论为什么大部分数据集完全移除比部分移除的效果略好？

从玄学走向科学：AB测试驱动的科学增长

​ 抖音二字就源自AB测试，是字节当时下载量排名第二的名称。

实验对象随机分流

• 实验对象如何随机分为实验组和对照组
• 实验量增加后，流量不够问题
• 不同层之间的正交性实现和保证

随机分流：哈希算法

​ 随机分流的随机性通过哈希算法实现的。哈希函数在对用户进行分组时只用到了用户标识，能够把有规律的id集合散列均匀，即众多属性如机型、地域、年龄等均匀分流。此外，哈希函数若输入值是固定的，则输出值也是固定的，可以保证用户不会跳组。

​ AB实验分流系统中常见的散列算法有MD5、SHA、Murmur等，其中Murmur算法在计算性能、抗碰撞性、均匀性和相关性较好，在工程实践中运用最多。

实验层技术&流量正交

​ 实验层技术为了让多个实验并行不互相干扰，且都获得足够的流量而研发的流量分层技术。实验层技术将总体流量“复制”无数遍，形成无数个流量层（但仍是同一批用户），让总体流量可以被无数次复用，从而提高实验效率。为保证各实验的结果不受到其他实验的干扰，各层流量是正交的。

​ 流量正交指每个独立实验为一层，一份流量穿越每层实验时都会随机打散再重组，保证每层流量数量相同又不互相干扰。通俗地讲，每层实验的实验组和对照组都平均的拥有其它层实验的实验组。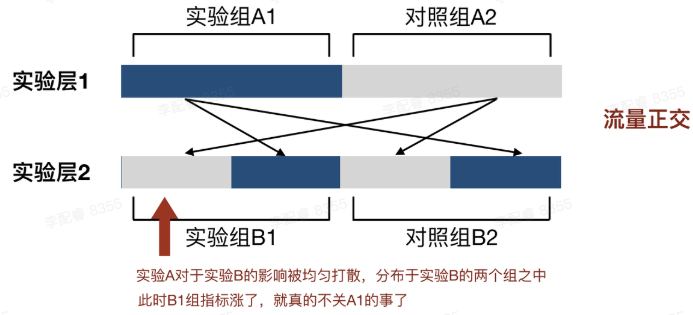

AB实验指标

• 核心指标
  • 决策实验功能是否符合预测的指标
    • 常见核心指标：转化率、留存率、人均次数类、平均值类
• 围栏指标
  • 必须守护的业务线指标
  • 实验功能一般不能对其有显著负向影响

广告场景下双边市场的实验设计

​ 双边市场是一个连接两个群体的平台，供给方和需求方。由于供给方和需求方的行为存在彼此影响（双边网络效应），导致AB测试中实验组和对照组难以满足独立性假设。互联网场景下，绝大多数平台都是双边市场。

​ 一般双边市场的实验可以通过地域随机化、类目随机化或时间随机化的方式将竞争隔离在地域、类目或时间段内部。但广告平台在地域和时间上都不具有可行性。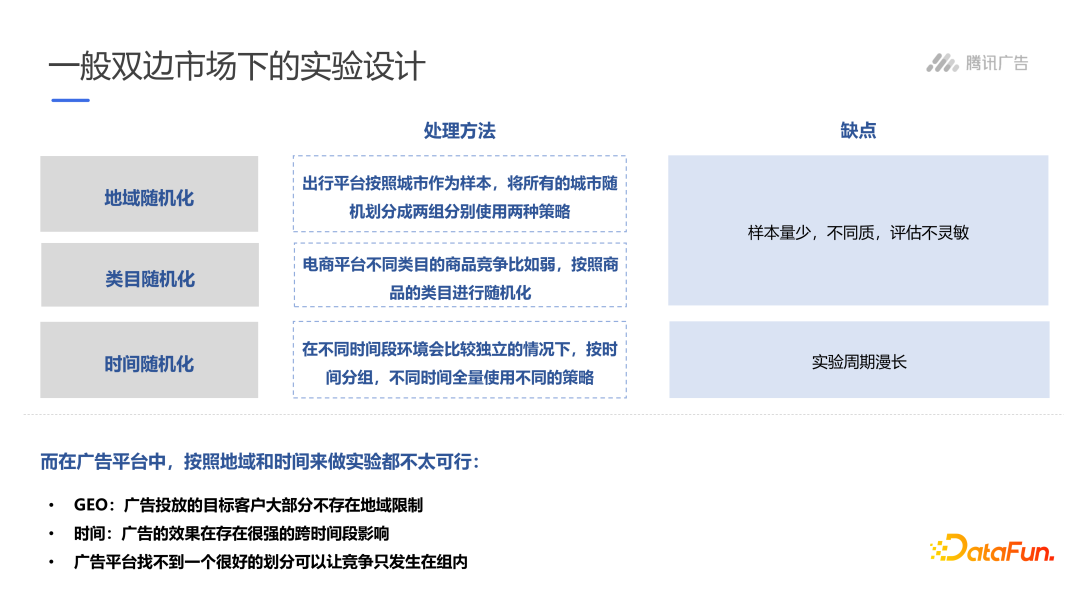

广告流量四表格实验

​ 一种思路是将大盘的流量与广告分别考虑成两个样本空间，并将流量和广告均分成两组，策略只在流量和广告都处于实验组时才生效。在实验开始前，预先将实验流量$UV_1$中曝光两分广告，假设每份有25个曝光，$UV_2$不做处理。实验中，将$AD_1\times UV_1$中加入策略，由于策略可能抢夺$AD_2\times UV_1$的流量，所以通过$y_{11}’=total_1-y_{22}$衡量策略的提升，其中$total_1$是处理后在实验组流量$UV_1$的曝光总数。

​ 理想状态下，没有抢夺和外溢。

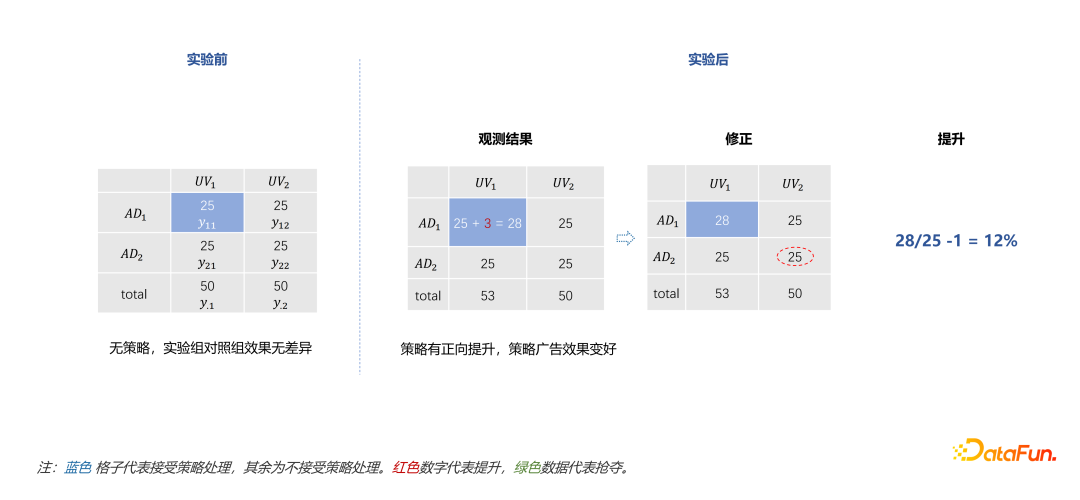
​ 只有抢夺没有外溢的情况下，用$y_{22}$衡量对照组才是合理的。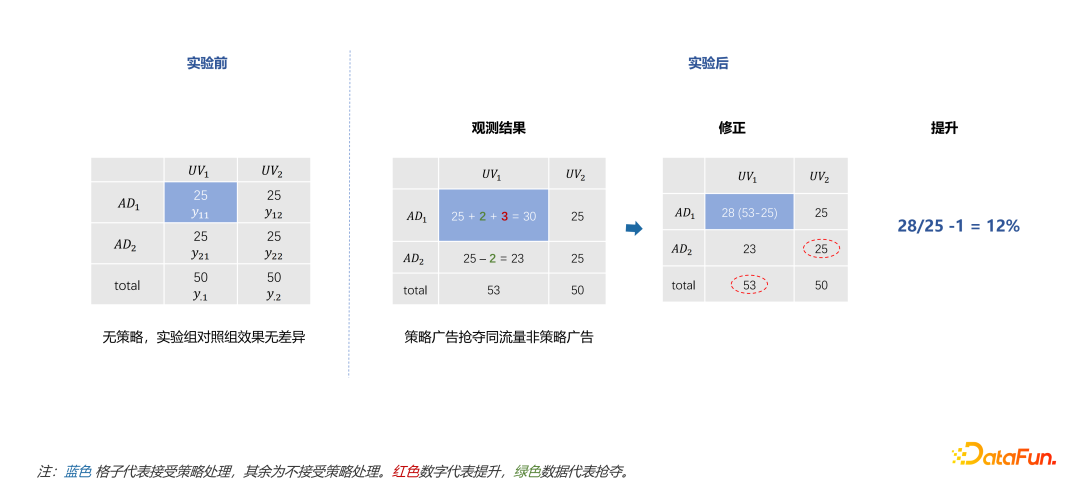

​ 现实中，很容易发生外溢现象，即$AD_1$对$UV_1$流量的策略效果外溢到了对照组$UV_2$中，使$AD_1\times UV_2$对$AD_2\times UV_2$也发生抢夺效果。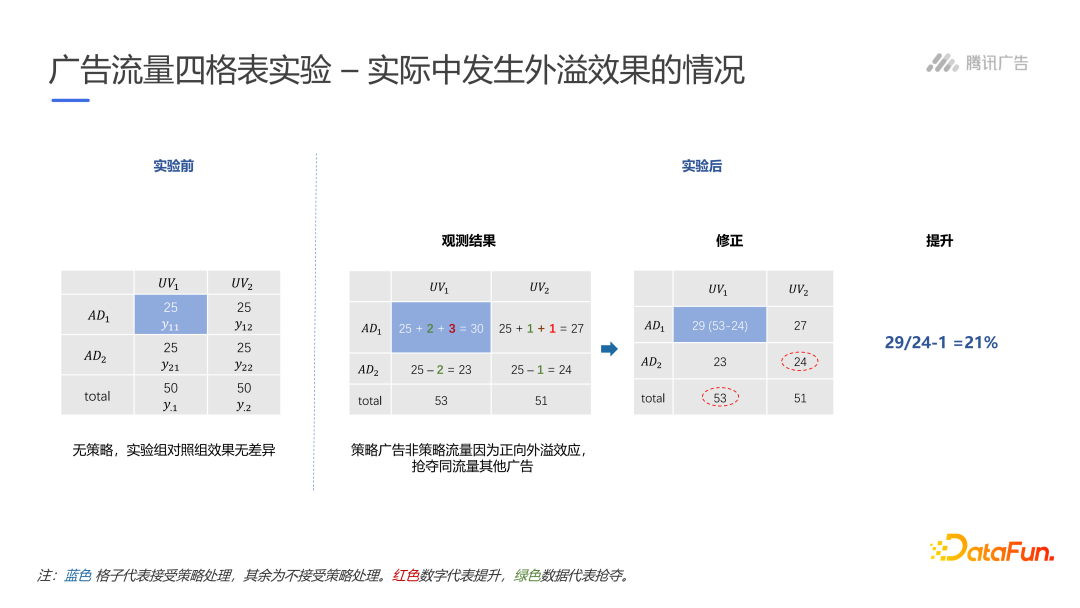

​ 在实际中，当存在传递效应或抢夺效应严重时，广告流量四表格实验一般无法得到确切效果。

隔离广告，避免外溢

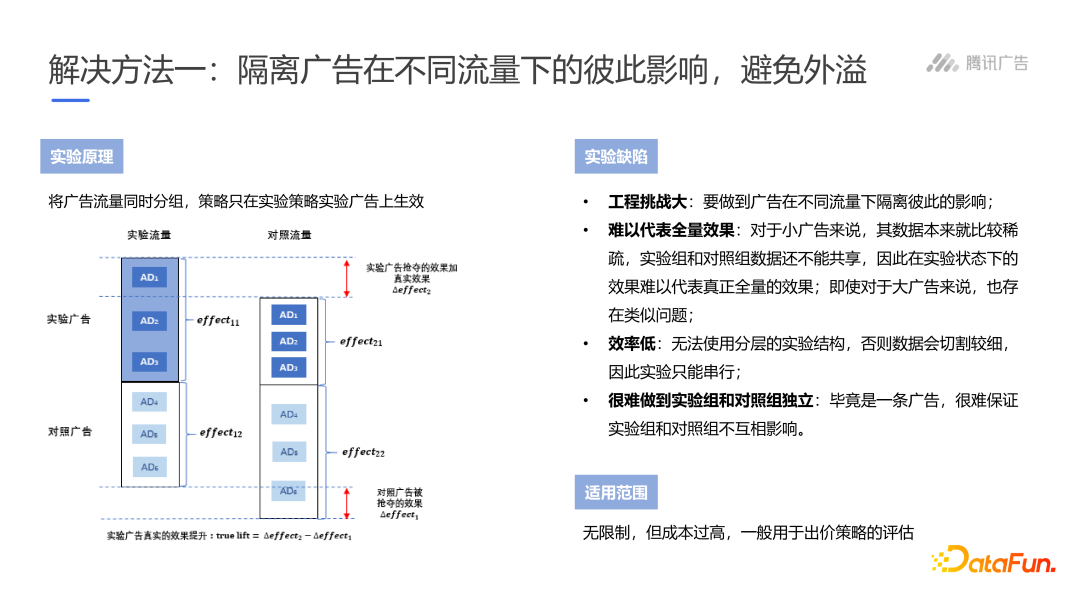
​ 执行难度较大，成本较高，效果差，效率低。

隔离广告和流量

​ 50%的流量召回50%的实验广告，另外50%流量召回50%对照广告。但我没有理解它是如何隔绝传递效应和抢夺效应的，但幸好它不合理。

改进方案

实验广告和对照广告同时流出到空白流量中。但问题是实验广告和对照光层仍然会在空白流量中竞争，存在抢夺和外溢，进而对实验、对照流量的结果产生影响，使得实验不准确。

广告分身流量联合实验

Facebook的Counterfactual interleaving实验

​ 实验设计可以分为两类，一种是between subject design一个样本只接受一种处理；另一种是within subject design一个样本接受两种处理。Facebook的Counterfactual interleaving实验本质是within subject design，对于一个请求通过两种算法召回广告，将全量广告分别使用实验策略和对照策略排序，最后将排名合并。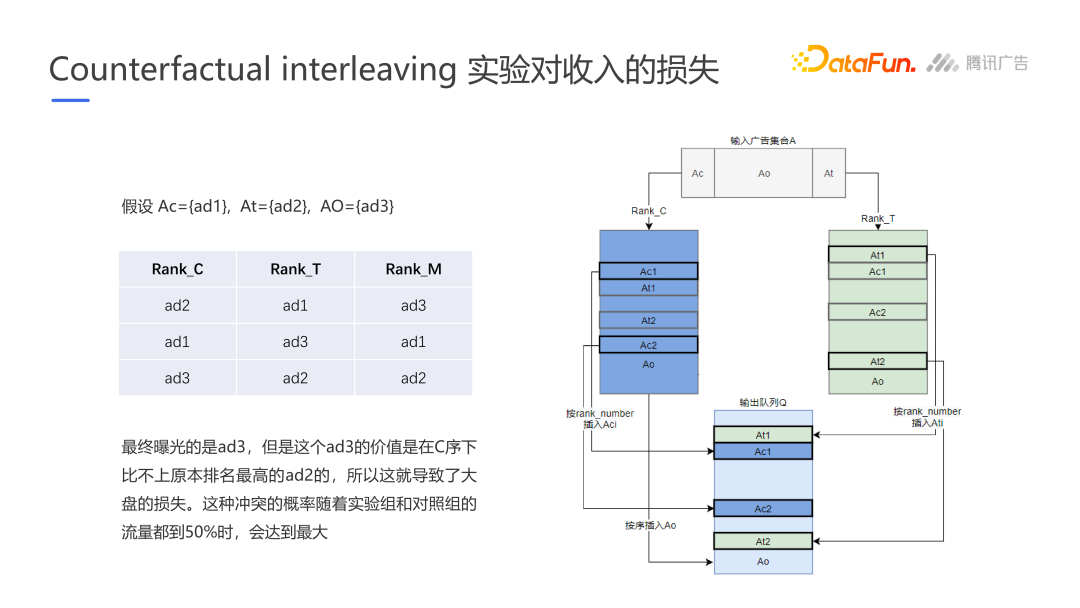

​ 这种算法存在3种缺陷：

• 康多塞悖论Condorcet paradox：当两个策略并行时，意味着存在3种排序方式，融合方式存在问题
• 本质上是有损实验方式，曝光的ad3在实验组和对照组都不是最高的
• 状态依赖带来污染

腾讯列联表联合采样

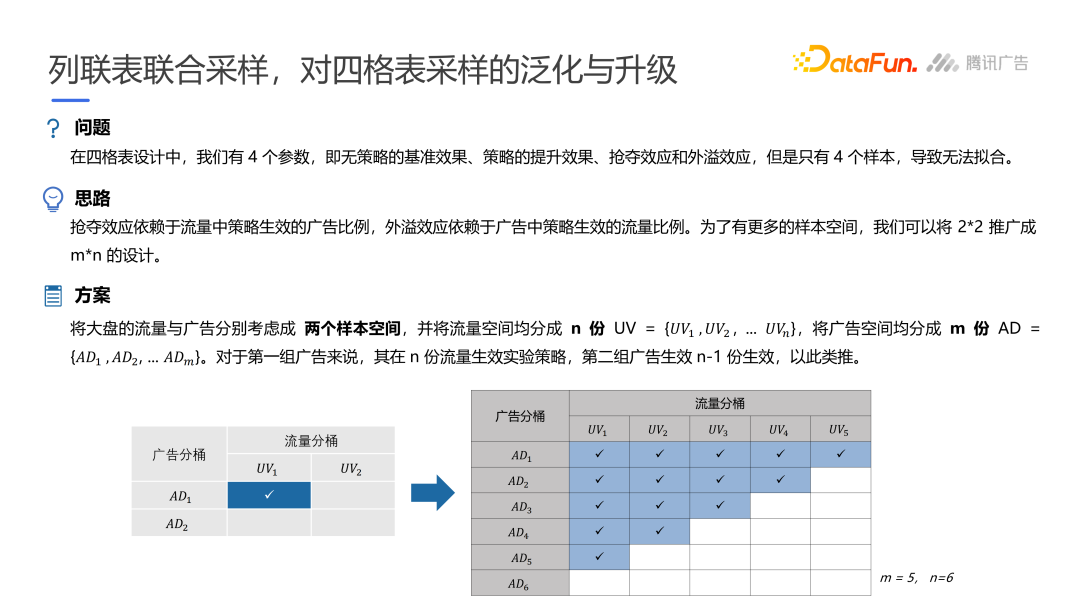
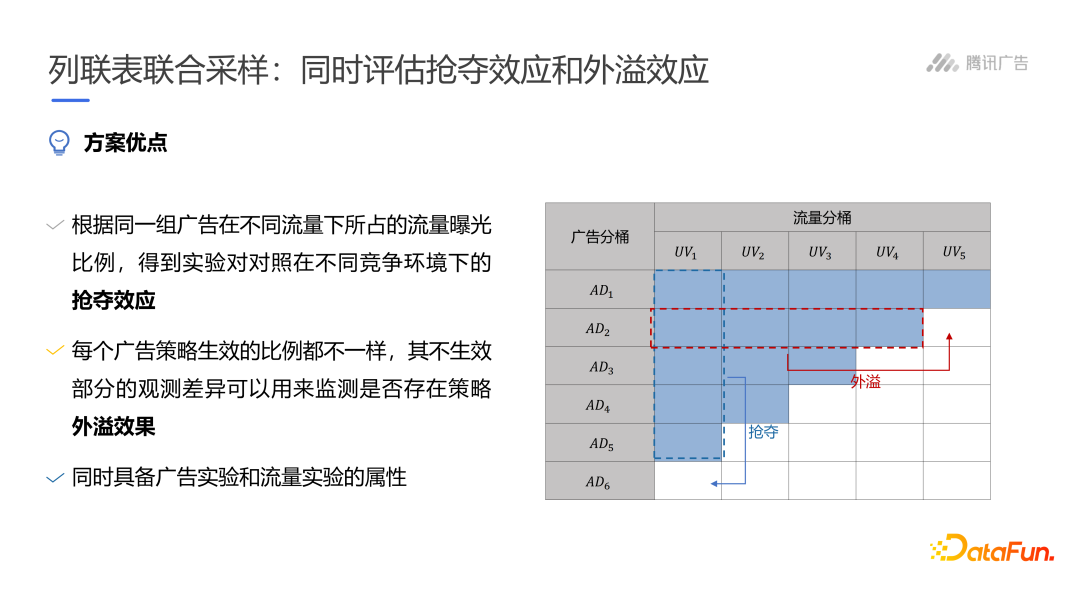
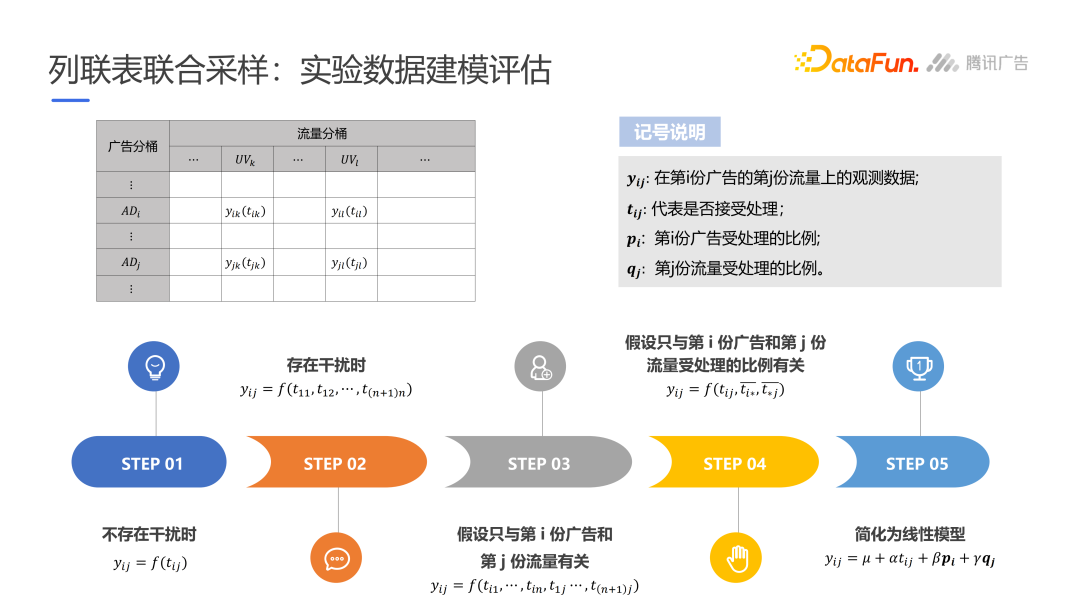
​ 构造线性模型拟合结果，分析协同和竞争。

基于话题标签（#）的社交媒体事件流行预测³

​ 在社交媒体上，我们很难用单一的类型（图像、话题标签或信息）去代表一个社会事件及它的所有观点。当我们考虑事件的所有细节时，由于社交网络上存在庞大的相关信息并且在快速演变，我们无法实现高效的事件流行预测工作。因此，一个合理的策略是选择话题标签作为复杂事件和信息之间的桥梁，它将事件及其相关内容总结在一个粗糙的水平。

​ 我们将时隙$t$的事件$E$流行程度定义为$P(E,t)$，表示当前时隙与事件相关的信息体量。事件$E$被视作信息集合$D_E={d_1, d_2,…,d_n}$和话题标签$H_E={h_1,h_2,..,h_m}$的结合，其中$d_i$包含一个属于$H_E$的话题标签子集$H_{di}$。任务是给定事件$E$和时隙$t$的信息集$d_i$，即事件相关话题标签子集$H_{d i}$，预测下一时隙的事件流行程度$P(R,t+1)$。

​ 前人曾经提出通过对事件流行状态分类、估计事件影响用户数量、话题标签代表事件和话题内信息数量等方式预测社会事件的流行程度，但这些方法都限制了使用单一属性，忽视了复杂社会事件各属性之间的相关性，因此在包含多重属性的复杂事件中效果均不佳。作者的方法重点解决3个问题：

• 开发新的社交媒体信息表示模型，使其对大量噪声和媒体稀疏具有稳健性
  • 大量噪声使有效的社交媒体信息十分稀疏
• 构建评估话题标签对事件影响的良好评估，进而选择种子标签
  • 通常事件带有大量话题标签，并且不同的标签对事件传播具有不同重要性
• 构建更先进的模型用于高效地事件流行预测，并且可以在信息流上良好维护
  • 动态社交媒体信息流会快速改变事件的多重属性和事件流行程度的关系
  • 保证算法NPC

文献综述

​ 社交媒体预测任务（Social media prediction，SMP）通常被用于评估个人信息（如住址），预测信息传播范围，分析社会事件对股价的冲击。

​ 其中，在事件流行范围任务上，图像、信息、回帖行为、相关推文或评论及阅读用户数量被认为是社交网络的关键属性。作者将现有的社交媒体流行性预测方法分为三类：

• 基于先验知识的方法
  • 预设内容流行性分为多个阶段，通过历史信息预测未来时隙归属哪个阶段
• 基于信息扩散的方法
  • 通过用户互动识别内容在社交媒体上的传播速度
  • 专注于挖掘用户对事件传播的影响
  • 忽视了至关重要的事件内容
• 基于预测模型的方法
  • 通过多类别特征构建模型
  • 发掘高度影响社交媒体事件传播预测的隐藏特征
  • 忽视了用户交互

解决方案架构

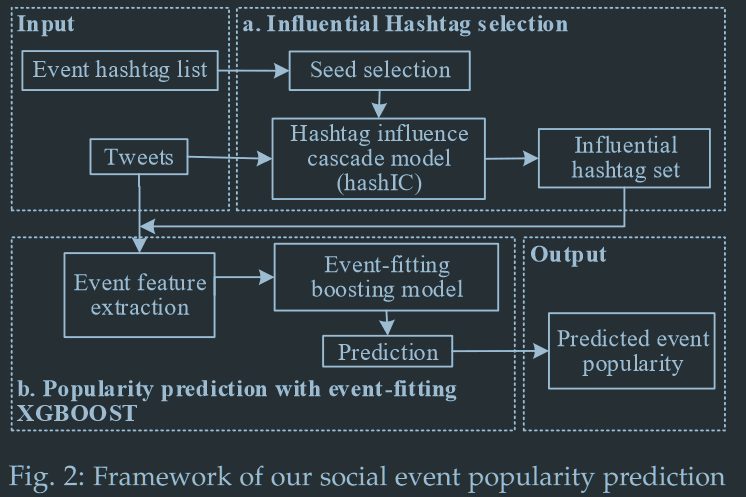
• 高影响话题标签选择
  • 从社会影响和内容影响两方面考虑成对话题标签相关性的2步法
    • 选取话题标签种子
    • 通过一个话题标签影响级联模型激活最终的高影响力标签
• 事件流行程度预测
  • Boosting模型

高影响力话题标签筛选

话题标签影响力

​ 给定话题标签$h$，如果只进行计数，则只能反应标签在当前时隙的流行程度（popularity influence ？），而没有反应用户交互等事件传播重要信息。作者提出三种方法测量话题标签影响力（influence）：

• 基于流行重要性（popularity importance-based）
  • 表明未来该标签影响的事件相关推文数量
  • $I^t_p(h)=\frac{N^t(h)}{N^t(E)}$
    • $N^t(h)$表示时隙$t$带有话题标签$h$的推文数量
    • $N^t(E)$表示时隙$t$事件$E$相关推文总数量
• 基于社交重要性（social importance-based）
  • 表明话题标签影响到的用户数量
  • $I_s^t(h)=\frac{U^t_n(h)}{N^t_u(E)}$
    • $U^t_n(h)$表示时隙$t$发表带有话题标签$h$的推文的用户数量
    • $N^t_u(E)$表示时隙$t$发表关于事件$E$推文的用户总数量
• 混合型（hybrid-based）
  • 综合考虑了流行程度和社交影响
  • $I^t(h)=w_p\cdot I^t_p(h)+w_s\cdot I^t_s(h)$

​ 具有高影响力的话题标签包括擅长于激活其他话题标签并影响事件的种子标签、更可能被种子标签激活并进一步影响事件的话题标签。

​ 作者还依靠2014世界杯数据集WC2014测试了三种测量指标的RMSE、MAE、MAPE，结果表明混合型效果最佳。

但问题是似乎该数据集并没有真实值？至少我没有看到作者交代。我没有想明白作者是如何计算的。此外，混合型的权重明显是需要训练的，作者目前还未交代。

种子话题标签筛选

基于排序的话题标签种子选取算法ranking-based hashtag seed selection（RHSS）

• 对话题标签集按影响力降序排列
• 提取top k话题标签

​ 但是由于标签之间可能存在相关性，top k话题标签可能不是最优的

基于相关性的话题标签种子选取算法correlation-based hashtag seed selection（CHSS）

​ 目的是选取的k个话题标签整体影响力最大化。

​ 给定话题标签集$H={h_1, h_2, …,h_n}$，标签集的影响力定义为$H_tSetInf^t(H)=w_p\cdot Inf^t_p(H)+w_s\cdot Inf^t_s(H)$，其中$Inf^t_p(H)=\frac{N^t(H)}{N^t(E)}$和$Inf^t_s(H)=\frac{U^t_n(H)}{N^t_u(E)}$，即话题标签集层次的混合型标签影响力。

​ 种子选取问题正式的描述为：给定一个事件相关话题标签集$H$，选取最佳的$H$的$k$话题标签子集，使得$\forall h_{sub}\in H,H_{sub}\neq H_{seed},|H_{sub}|=|H_{seed}|$总有$H_tSetInf(H_{sub})\leq H_tSetInf(H_{seed})$。

命题1：话题标签的最优种子集选取为NP-complete问题

证：作者通过两步法将该算法简化为经典的NPC问题Subset Sum Problem。

${\boxed{\begin{aligned}子集&和问题SSP \\ &给定包含n个正整数的集合S=(s_1,s_2,…,s_n)和正整数M\\ &寻找是否存在W的一个子集I，使得I中元素和为M\\ \\ &若采用遍历的方法，时间复杂度为O(n^2)，即NP问题\\ &采用动态规划可简化为NPC问题\\ &考虑sub(i,j)为S中前i个元素的子集和等于j的情况，则\\ &\ \ \ \ \ \ \ 若S_i>j，则S_i不在子集sub(i,j)中\\ &\ \ \ \ \ \ \ 若S_i\leq j\\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ 若S_i不在子集sub(i,j)中,则sub(i,j)=sub(i-1,j)\\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ 若S_i在子集sub(i,j)中,则sub(i,j)=sub(i-1,j-S_i)\cup S_i\end{aligned}}}$

​ 令$\mathbb{S}$为SSP问题的所有子集的集合。第一步构建$\mathbb{H}$作为最优种子集选取问题的所有子集的集合，并使得$|\mathbb{S}|=|H|$，且存在$H_i=f(S_j)$的$\mathbb{S}$到$\mathbb{H}$一一映射$f$。该映射可在多项式时间内完成，$O(|\mathbb{S}|)$。第二步，给定子集大小$|H_i|$，选取子集中最优的一个（影响力最大/子集和最大），显然可在多项式时间内完成，$O(|H_i|)$。

​ $\therefore$命题得证

​ 当最优种子集不能在合理时间内识别时，作者提出了借助贪婪方法进行近似估计的三步法。

• 将事件相关话题标签按影响力高低降序排列，将影响力最高的标签作为第一个种子
• 从剩余话题标签中选取一个标签加入种子集，使当前种子集影响力最大化
• 重复第二步，直至$k$个种子被选定

​ 近似估计的理论保证：给定一个非负、单调的次模函数$f$，由次模函数性质可知贪心算法获取的近似解$S_{approx}$相对于最优解$S_{optimization}$有$f(S_{approx})\geq(1-\frac{1}{e})f(S_{optimization})$，其中$1-\frac{1}{e}$为近似因子。

​ 接下来证明CHSS算法为次模函数且单调。

​ 约定：给定事件相关话题标签集$H={h_1,…,h_n}$

• $H_{sub}$为话题标签集$H$中$k$个标签的子集
• $H_{tem}$为子集$H_{sub}$中带有$m$个标签的子集
• $S(h)={d_1,d_2,…,d_n}$为带有话题标签$h$的推文集
• $S_u(h)={u_1, u_2,…,u_n}$为带有话题标签$h$的用户集
• $\therefore |S(h)|=N(h)$即带有话题标签$h$的推文总数
• $\therefore |S_u(h)|=N_u(h)$即发布带有话题标签$h$推文的用户总数

对话题标签集$H={h_1,h_2,…,h_n}$，有$S(H)=S(h_1)\cup S(h_2)\cup…\cup S(h_n)$和$S_u(H)=S_u(h_1)\cup S_u(h_2)\cup…\cup S_u(h_n)$

​ 由于一条推文可以对应多个话题标签，一个用户可以发布多个话题标签的推文，$\therefore |S(H)|\leq\sum\limits_{i=1}^{|H|}|S(h_i)|\ and |S_u(H)|\leq\sum\limits_{i=1}^{|H|}|S_u(h_i)|$

​ 由于$H_{tem}\subseteq H_{sub}$，所以$S(h)-S(H_{tem})\supseteq S(h)-S(H_{sub})$

定理2：话题标签集影响力函数$H_tSetInf(\cdot)$是次模函数

​ 即欲证：$H_tSetInf(H_{tem}\cup {h})-H_tSetInf(H_{term})\geq H_tSetInf(H_{sub}\cup {h})-H_tSetInf(H_{sub})，\forall h\in H成立$

证：${\boxed{\begin{aligned}&\because \forall 集合A、B，有A-B=A\cup B-B\\ &且S(h)-S(H_{tem})\supseteq S(h)-S(H_{sub})\\ &\therefore S(h)\cup S(H_{tem})-S(H_{tem})\supseteq S(h)\cup S(H_{sub})-S(H_{sub})\\ &\therefore|S(h)\cup S(H_{tem})-S(H_{tem})|\geq|S(h)\cup S(H_{sub})-S(H_{sub}|\\ &又\because|A\cup B-B|=|A\cup B|-|B|\\ &\therefore |S(h)\cup S(H_{tem})|-|S(H_{tem})|\geq|S(h)\cup S(H_{sub})|-|S(H_{sub})|\\ &同理|S_u(h)\cup S_u(H_{tem}) |-|S_u(H_{tem})|\geq|S_u(h)\cup S_u(H_{sub})|-|S_u(H_{sub})|\\ &\therefore \frac{w_p}{|N(E)|}|S(h)\cup S(H_{tem})|-\frac{w_p}{|N(E)|}|S(H_{tem})|\geq\frac{w_p}{|N(E)|}|S(h)\cup S(H_{sub})|-\frac{w_p}{|N(E)|}|S(H_{sub})|\\ &\frac{w_s}{|N_u(E)|}|S_u(h)\cup S_u(H_{tem})|-\frac{w_s}{|N_u(E)|}|S_u(H_{tem})|\geq\frac{w_s}{|N_u(E)|}|S_u(h)\cup S(H_{sub})|-\frac{w_s}{|N_e(E)|}\\ &合并\therefore H_tSetInf({h}\cup H_{tem})-H_tSetInf(H_{tem})\geq H_tS etInf({h}\cup H_{sub})-H_tSetInf(H_{sub})\\ &\therefore 次模性得证\end{aligned}}}$

定理3：话题标签集影响力函数$H_tSetInf(\cdot)$是单调函数

​ 即欲证$H_tSetInf(H_{sub}\cup {h})\geq H_tSetInf(H_{sub})，\forall h\in H-H_{sub}$成立

证：${\boxed{\begin{aligned}&\because S(H_{sub})\cup S(h)\supseteq S(H_{sub})\&且S_u(H_{sub})\cup S_u(h)\supseteq S_u(H_{sub})\\ &\therefore|S(H_{sub})\cup S(h)|\geq|S(H_{sub})|\\ &且|S_u(H_{sub})\cup S_u(h)|\geq|S_u(H_{sub})|\\ &\therefore\frac{w_p}{|N(E)|}|S(H_{sub})\cup S(h)|\geq \frac{w_p}{|N(E)|}|S(H_{sub})|\\ &且\frac{w_s}{|N_u(E)|}|S_u(H_{sub})\cup S_u(h)|\geq\frac{w_s}{|N_u(E)|}|S_u(H_{sub})|\\ &合并\therefore H_tSetInf(H_{sub}\cup{h})\geq H_tSetInf(H_{sub})\\ &\therefore H_tSetInf(\cdot)函数单调不减 \end{aligned}}}$

$\therefore$命题2和命题3保证了命题1中近似估计的成立

高影响力话题标签级联模型

​ 话题标签选择的目的是获取事件$E$所有话题标签集$H_E$的一个子集$H_s$，使之包含该事件的最有影响力的话题标签。解决该问题的常用做法GNN等神经网络模型和独立级联模型IC，由于神经网络模型时间开销过大，作者在独立建联模型IC的基础上设计了高影响力话题标签级独立联模型HashICM。该模型在独立级联模型的基础上，通过嵌入一组事件相关的社交媒体上话题标签及其话题分布，扩展了从用户影响力估计到话题标签的选择。

​ 给定事件$E$，HashICM模型首先构建话题标签图模型，之后激活有影响力的话题标签。

话题标签图模型

​ 在时隙$t$，关于事件$E$的加权无向图$G(E,t)$表示未$(H_E,E(H_E))$，其中$H_E$为话题标签组，$E(H_E)$为加权边的集合，表示顶点（话题标签）之间的相似度。

​ 作者使用皮尔逊相关衡量话题标签的相似度，给定项的标签对$(h_i,h_j)$，其相似度$Sim(h_i,h_j)=Pearson(f_{h_i},f_{h_j)}$，其中$f_{h_i}$和$f_{h_j}$为分别从话题标签$h_i、h_j$中提取的归一化向量表示。

​ 给定话题标签$h_i$，作者通过连接3类特征，即内容特征、社交特征和由MGe-LDA模型推断的主题分布特征$h_i$，构成话题标签的特征向量$f_{hi}$。

• 内容特征

  • 通过信息的统计信息提取

  • 为克服话题标签稀疏问题，创建了话题标签词社区，包含所有与该标签共享相同信息的词，用于提取词社区级别的特征

  • 同样，构建了话题标签社区，包含共享相同信息的话题标签，用于提取话题标签社区级别的特征

  • 作者没有交代如何构建这些社区

  • 

• 社交特征

  • 

• 全局特征

  • 基于祠社区的TF-IDF向量
  • MGe-LDA模型⁴，一个话题标签相关的社交事件检测模型，获取话题标签主题分布

• 所有特征均归一化到二范数空间

话题标签独立级联模型

• 将所有种子初始化为激活状态，并加入结果高影响力话题标签集result
• 新的高影响力话题标签通过递归激活临近标签获取，直至没有新的标签
  • 将所有激活标签$h$添加至result
  • 基于$h$与其所有未激活邻居的相似度，降序排列未激活邻居
  • 获取$h$主题分布的最大概率主题
  • 依据邻居$n$的主题分布获取该话题的概率，作为激活概率$P$
  • 以$P$的概率激活邻居标签
  • 若话题标签激活，则加入result
  • 若没有新的话题标签产生，停止迭代
• 返回result

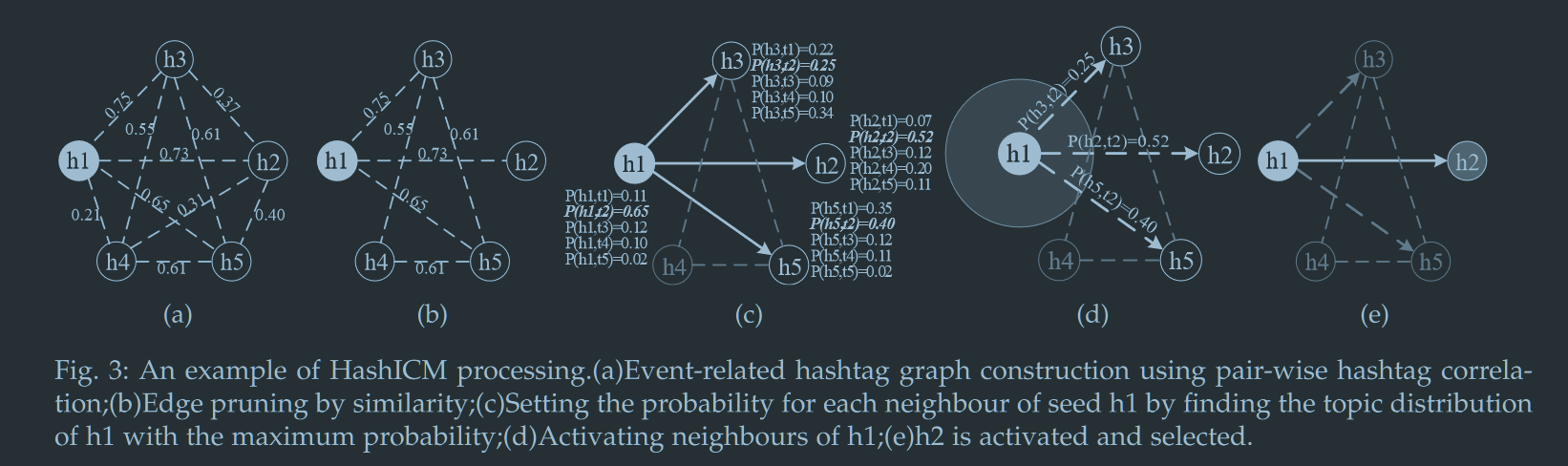
​ 以可视化形式详细说明HashICM算法。

• 构建给定时隙种子$h_1$与所有事件相关话题标签的图模型
• 计算话题标签之间的相似度，将低于阈值0.5的边剪枝
• 根据主题分布计算$h_1$对相邻节点$h_2,h_3,h_5$的激活概率
• 激活（本案例中$h_2$激活概率最高，且被成功激活）

XGBOOST模型流行度预测

​ XGBOOST算法效率高且可以自动处理特征稀疏性。

事件特征提取

​ 前人通常采用提取社交和内容特征来预测事件流行程度，作者补充了话题标签特征。本研究从带有高影响力话题标签的推文中提取事件特征，角标$_t$为内容因素，角标$u$为社交因素，角标$_h$为话题标签因素。

事件拟合流行度预测

​ 给定事件$E$，通过时隙$t$带有高影响力话题标签的信息获取特征$F(E,t)={f_1,…,f_m}$。

​ 对每个特征$f_i$通过线性回归进行交叉学习cross learning，即将$f_i$视作基本事实，通过特征$F(E,t),f_i\notin F(E,t)$学习$f_i$对事件$E$的重要性。损失函数采用最小二乘。目标函数为$L_{f_i}=w^T_{f_i}(F(E,t)+b),f_i\notin F(E,t)$，进而获得权重向量$w_{f_i}={w_1,w_2,…,w_{m-1}}$。特征$f_i$的重要性通过平均权重获得$w(f_i)=\frac{\sum_{j=1}^{m-1}w_j(f_i)}{m-1}$。所以加权事件特征为$F_w(E,t)=w(f_i)\times f_i$。

​ 进而可以通过加权事件特征构建XGBOOST模型，预测事件流行程度$Log(P(E,t))$。

有必要人工加权吗？优势在哪里？

动态预测模型维护

• 何时更新模型
• 如何增量的更新模型

​ 针对第一个问题，我们需要识别事件传播结构的阶段周期。而Locally linear embedding algorithm（LLE）作为识别高维数据非线性结构的无监督学习算法被证明能够捕捉话题-事件传播结构的情况。作者在每个时隙$t$对事件相关话题标签的内容特征和社交特征应用LLE算法，而由于只在较短时隙内分析，所以更稳定、更长期的全局特征在此处不予考虑。

​ 具体地，给定事件$E$，在时隙$t$的话题标签集$H_E^t={h_1,h_2,…,h_n}$中每个话题标签$h\in H_E^t$有特征集$f_h={f_1,f_2,…,f_m}$。首先构建事件$E$在时隙$t$的话题标签特征矩阵$M_E^t$，其中rows为根据影响力降序排列的时间相关话题标签$H_E^t$，每个元素是对应的特征值。$M^t_E$为$n\times m$矩阵，对此应用LLE算法降维，获取的$n$维向量反应了隐含的事件结构。因此，事件维护的传播结构为$S_{w_E^t}={s_E^{1},…,s_E^{t_s}}$，其中$t_s$为滚动的当前时间窗口大小。给定时隙$t$和事件结构$S_E^t$，以及当前时间窗口的事件传播结构$S_{W_E^t}$，事件$E$在时隙$t$的演进相似度 被量化为$E_{vl_E^t}=\frac{\sum_{i=1}^{t_s}Sim(S^t_E,S_E^j)}{t_s}$，其中$S^t_E={S_E^1，…,S^{t_s}_E}$。若演进相似度小于阈值$\phi$，预测模型将会被更新。

​ 更新模型在原有决策树的基础上追加新的决策树。

实验估计

​ 数据集为自2014年六月1日至2014年六月30日的45m英文推特，期间主要发生了Much Music Video Awards和2014世界杯。作者保留了712个世界杯相关标签和417个MV奖话题标签及包含#retweet,#followtrain等停止标签的噪声集。

​ 基准模型包括HashPRE、EventPRE、TSBP、CNN。HashIP-G为采用贪恋选取种子方法CHSS的模型，HashIP-S为采用top-k选取种子的RHSS的模型，HashIP-R为随机选取种子的模型。

​ 模型评价指标采用RMSE、MAR和MAPE。之后作者通过配对t检验比较提出模型和现有模型的表现差异。

效用估计

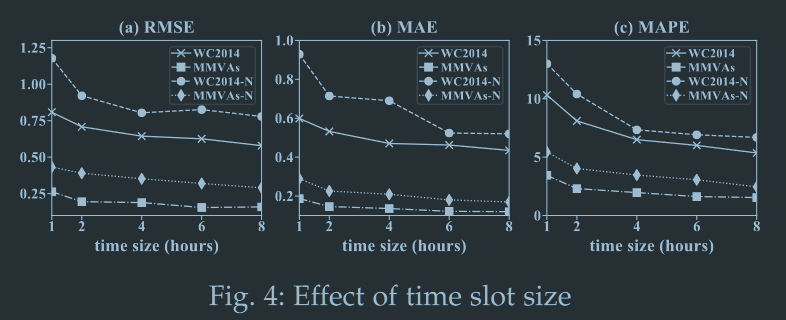
• 最佳时间窗口大小设定为6小时

  

• 同理，最佳种子大小$\gamma$在MMVAs中被设定为0.75%，在WC2014中被设定为0.045%

• 种子选择方法即HashIP-R、HashIP-S、HashIP-G中，top-k方法和贪婪方法表现明显优于随机选种和不选种，两个方法效果接近。

• 动态模型维护的阈值越高，模型更新越频繁，trade-off的结果是0.6

  

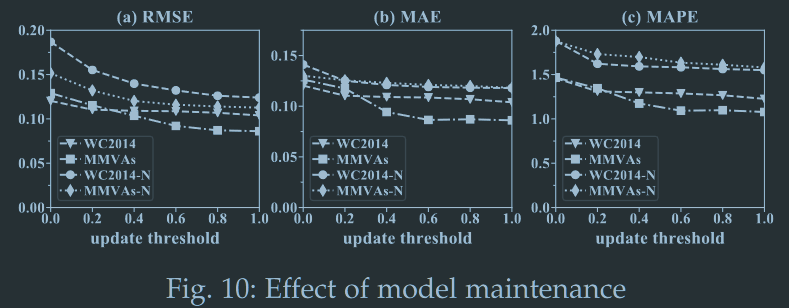
• 模型效果比较

  

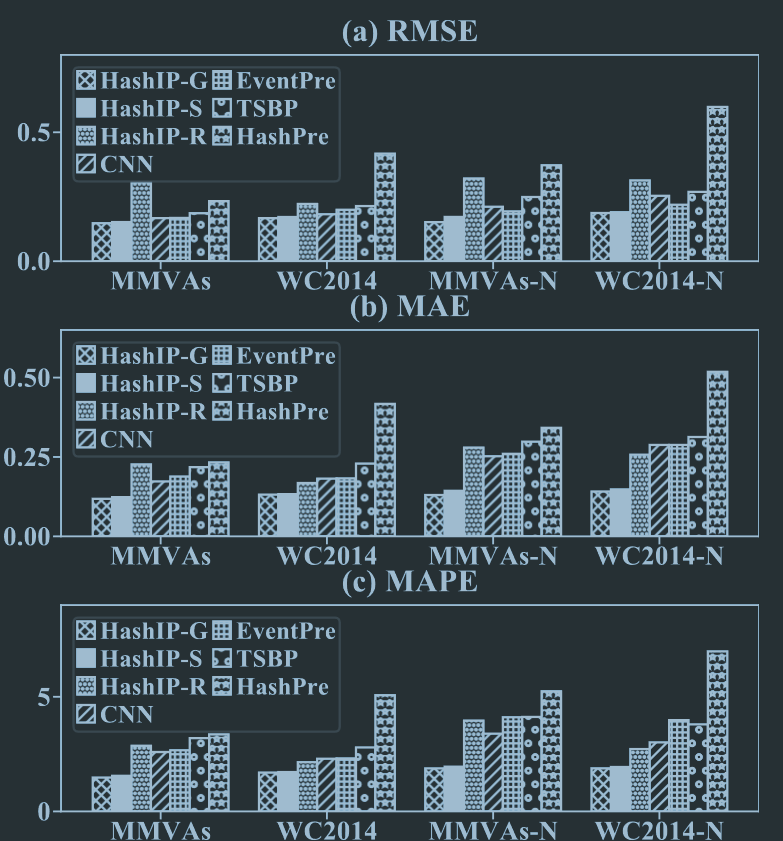
• 预测值与真实值差异

  

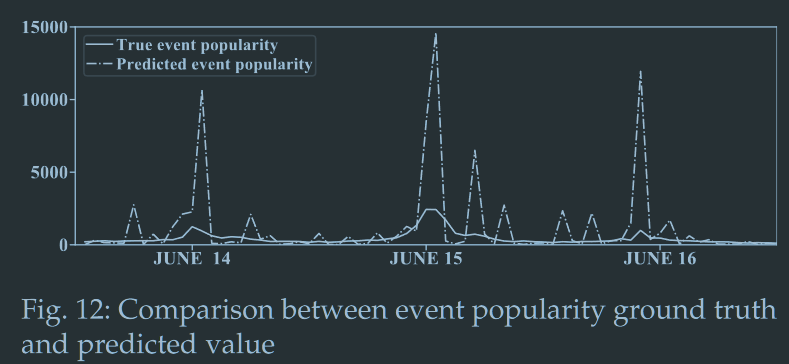
  误差还是比较大的，不过形状还是值得玩味的

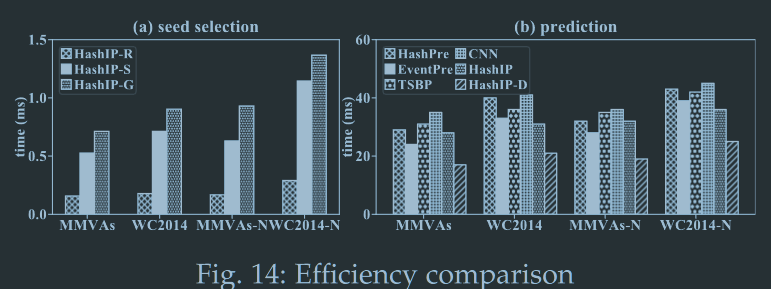
效率估计

• 种子选取算法上，top-k方案和贪婪方案均明显慢于随机选种，但在测试数据集上仍能被视作实时选种，延迟在ms级别
• 预测效率上，HashIP算法单次预测与现有算法耗时接近，而考虑动态更新后，HashIP算法显著优于其他算法
• 数据集大小对预测效率影响较小

美丽遇见德鲁克（十二）：拯救被侮辱与被损害的营销

​ 源自王茁老师关于彼得·德鲁克思想和化妆品行业的思考。我之前有读过王茁老师的著作《美丽洞察力》，里面详细地讲述了JTBD理论在化妆品行业的实践应用，受益匪浅。这次的MKT被污名化也是很多中国市场学者长期关注的话题，例如中山大学的卢泰宏老师就倾向于直接使用英文Marketing来称呼市场营销，并多次发文倡议市场营销专业改名。这次王茁老师从《营销管理》第16版出发，从理想和现实两个角度，对比分析MKT（特别是中国的MKT）是如何被侮辱与损害的。

​ 首先，回归营销的基本定义，目前AMA和《营销管理》采用的定义是“市场营销是创造、传播、传递和交换对顾客、客户、合作者和整个社会有价值的市场供应品的一种活动、制度和过程。”这意味着MKT必须坚持外部视角和顾客视角，即MKTer是在企业里做消费者那把椅子的人。这一想法早在70年前就被彼得·德鲁克提出了，但直至今日它仍不能实质上被管理者接受。德鲁克曾经有一个讽刺的比喻来描述很多所谓的“市场观念”其实难副其实，“挖墓人无论如何都还是挖墓人，尽管人们可能美名其曰‘殡葬业者’——只不过下葬的费用会上涨而已。”王茁老师借此来形容业界许多销售经理被更名为“营销副总裁”的现象，真正变化的不过是成本和工资罢了，“私域”、“全域”这些大热的企业概念癌愈发令人担忧。人们应该记住《为成果而管理》中的一段话：顾客很少会购买企业推销的产品，没有人会花钱买产品，人们真正花钱买的是自己所获得的满足感。

​ 其次，王茁老师强调企业MKT必须超越推销，“营销的目的是让推销显得多余”。然而，事实却是中国的很多企业，甚至是绝大部分企业在用推销的勤奋（天天促销）来掩盖战略的懒惰（洞察客户、打磨产品）。如消费者权益保护这些营销口号喊了多年，但从未被付诸实践，“消费者权益保护是‘营销的耻辱’”。

​ 最后，社会责任应该是市场营销的主要使命之一。企业的营销和创新可以分为两种，一种解决消费者的问题，让人们的生活更加轻松舒适；另一种激发人们的欲求，造成过度消费和对环境的破坏。经营者应该努力做好二者的平衡，并非所有新想法都值得推广。

​ 王茁老师指出，中国很多企业的问题都出在重推销、重促销，从未重营销。

彼得·德鲁克总结的营销五宗罪（1993年，《华尔街日报》）

• 追求超高利润和过于追求溢价
  • 会为竞争对于创造一个平替市场
• 贴着市场的容忍度收费
• 采用成本驱动的定价法
  • 德鲁克建议根据顾客可接受价格控制成本，而非成本定价
• 聚焦过去的成功
• 把解决问题的优先性置于把握机会之上

四个教训：

• 收买顾客不管用
• 不能只关注品类竞争，不关心需求竞争
• 只关注自己的顾客，不关注整体市场的顾客
• 忽视人口数量和结构的变化

科特勒的营销十宗罪（2014年）

• 企业没有充分做到以市场为中心和以客户为驱动
• 不充分了解目标顾客
• 需要更好的定义和监测其竞争对手
  • 忽略了远距离竞争对手和颠覆性技术
  • 缺少收集和发布竞争情报的系统
• 没有恰当地管理与利益相关者的关系
• 不善于寻求新机遇
• 营销策划过程存在缺陷
  • 没有范式和结构，绩效不可评估，没有应急计划
• 产品和服务政策需要收紧
  • 过度、无序扩张
• 缺乏21世纪营销技巧
• 没有最大限度地利用技术

业界动态

InfoQ：中国软件技术发展洞察和趋势预测报告2023

利益相关：InfoQ是致力于为 开发者 提供帮助的在线新闻/社区网站

调研问题：2022年重要技术发展回顾与2023年去世预测

调研对象：130+细分技术领域的技术专利数量、技术诞生时间、技术舆论指数、技术融资时间x

调研方法：桌面研究（二手资料研究）、专家访谈

调研结论：（该报告有“调”无“研”）

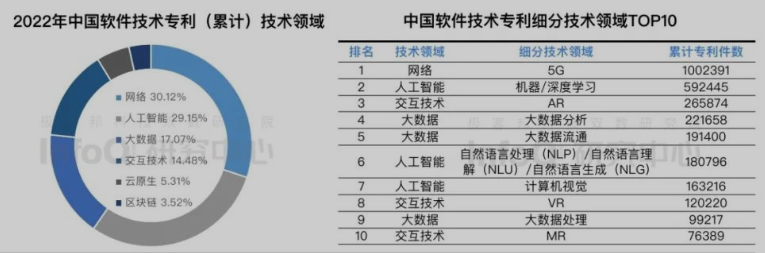
• 人工智能、大数据、云原生为2022年主要技术热词；中国网络和人工智能、大数据专利数量占比76.34%，云原生专利较少；
• 技术领域融资聚焦早期融资；云计算和人工智能融资赛道火热
• 云基础设施覆盖率提升，云应用受市场管局
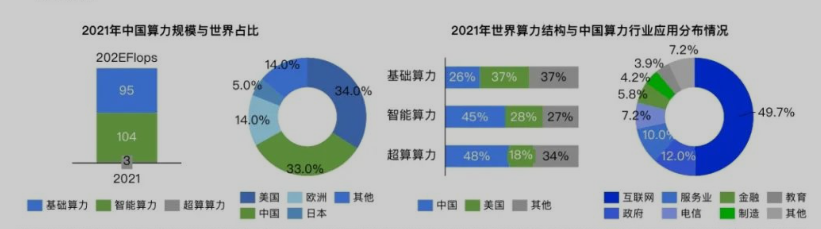
• 算力应用领域扩展，但行业采用程度有待进一步提升
• AIGC引发热议
• 数字孪生走向应用
• 虚拟世界内容在逐步推进；虚拟数字人认知度提升
• 工业互联网网络层、数据层、平台层、应用层多层推进
• 能源互联网开始构建
• 2023年趋势预测
  • 云上基础设施日益完善
  • 平台工程提升研发效能
  • 算力基础建设已取得明显成效，基础资源优化与调度服务成为主要阶段内容
  • 量子计算引领算力再升级
  • 数字世界和现实世界进一步打通
  • 应用需求增大，行业发展从强政策导向向部分市场导向转变

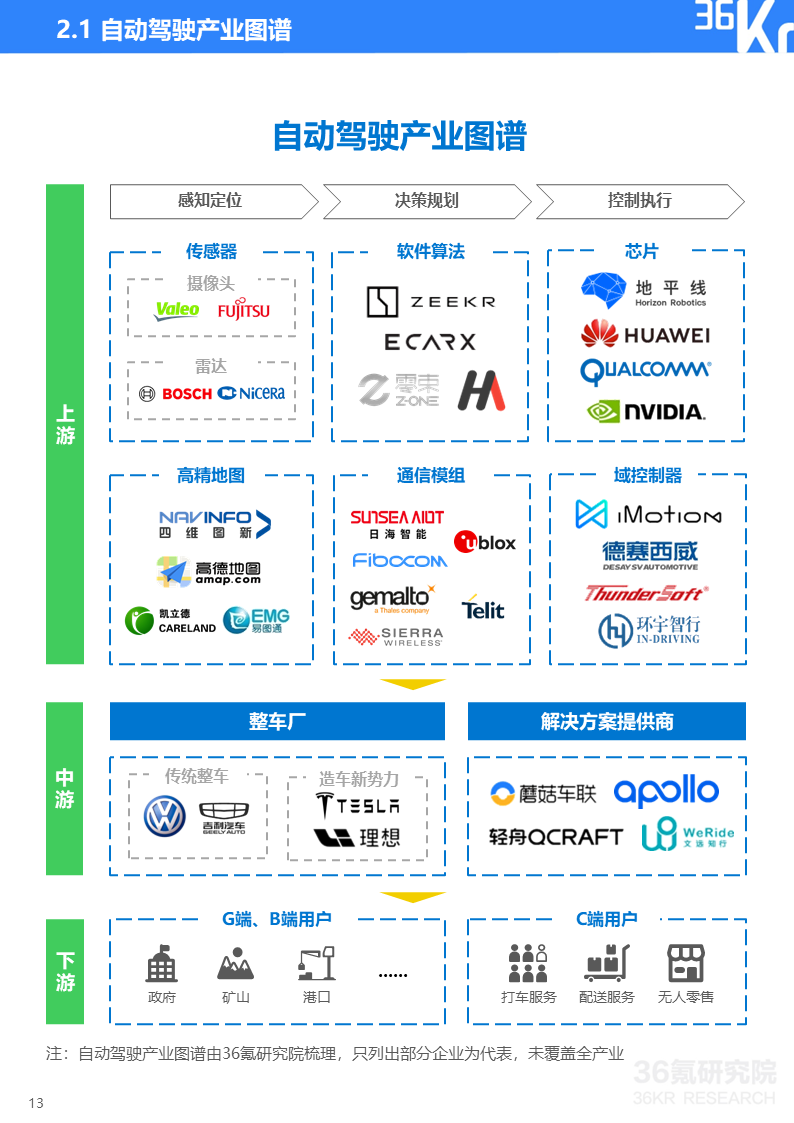
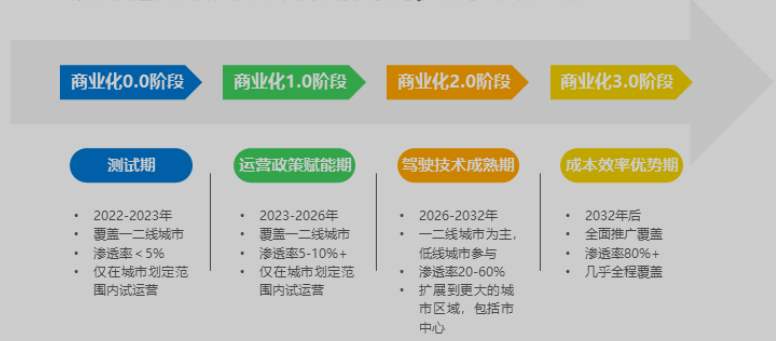
36氪研究院丨2023年中国自动驾驶行业研究报告

调研问题：

调研对象：国家政策、地平线/蘑菇车联/轻舟智航/知行科技企业

调研方法：二手资料研究、案例研究

调研结论：政策导向强；乘用车自动驾驶由L2向L3+过渡，商用车自动驾驶进入商业化运营阶段；商业化落地成为竞争关键

• 近年感知和决策算法突破提高了AI模型鲁棒性、系统冗余性和测试完善性。
• 2022年我国在售新车L2渗透率为35%，L3渗透率为9%
  • 预计2023年L2渗透率达51%，L3渗透率达20%
  • 部分企业在测试L4，目前渗透率2%
• 限定场景下的商用车自动驾驶进入商业化阶段
  • 对价格敏感度更低，B端付费意愿更高
  • 场景复杂度较低，政策扶持强
  • 干线物流、矿区、港口、机场、物流园区为主要发展场景
• 参与者包括传统车企、造车新势力、互联网/科技公司
  • 国际巨头多采取传统渐进式路线
  • 互联网/科技公司以AI算法和软件技术优势进入自动驾驶领域
• 单车智行和车路协同路线并行
• 2022年融资数量增加，融资金额大幅下降，资本市场趋于理性
• 
• 芯片CPU+ASIC方案有望成为未来主流方案
  • 批量定制的低功耗、低成本专用自动驾驶AI芯片ASIC有望逐步替代高功耗的GPU
  • 高算力不再稀缺，地平线、大华股份等国产芯片凭借低功耗、低成本、性能稳定、量产快等特点快速提升份额
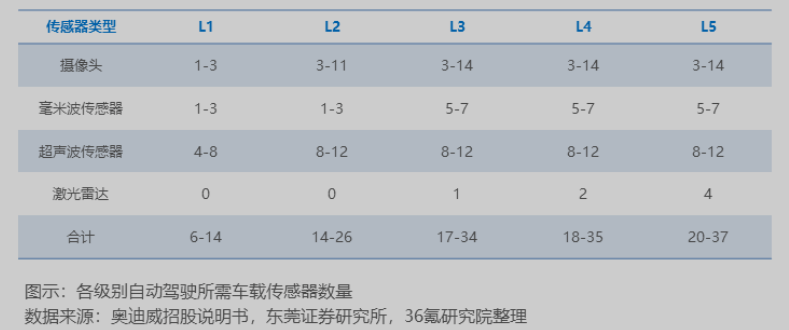
• 传感器：视觉派和雷达派路线对传感器需求均有增长
• 线控底盘和高精度地图是L3以上自动驾驶的关键
  • 高精度地图测绘存在政策限制
    • 导航电子地图制作（甲级）资质的20+单位均为国内企事业单位
• 车联网V2X产业环境逐渐成型
• 干线物流自动驾驶或可降低重卡运营成本26%，事故率80%，自动驾驶竞争激烈
• 末端物流通过自动驾驶无人配送车作为解决路线，目前开始小规模量产
• 环卫自动驾驶市场参与者众多
  • 技术、算反、数据积累、运营能力成为竞争关键
• 矿区自动驾驶初期测试
  • 我国起步较欧美晚
  • 基本聚焦于露天矿运输场景
• 港口运输自动化有自动引导运输车AGV、自动驾驶跨运车、自动驾驶集卡三种解决方案
  • 预计2025年中国集卡L4自动驾驶渗透率将超20%，达全球市场30%
• Robotaxi处于商业化测试阶段

技术技巧

R包：modelsummary多模型做表导出

​ 可以便捷地将多个模型整理成表格，包含置信区间，也可以将模型系数作森林图可视化。

R包：ggstats辅助ggplot2对统计量作图

​ ggstats版本的森林图。

娱乐

外星生命或智能摆在面前，你能认出来吗？——“梯径”提供的思路⁵

​ 人们总是在寻找外星人，并假设当它们出现在我们面前时，我们总是可以认出它们，但事实真的是这样的吗？

1996年，南极发现的火星陨石Allan Hills 84001上存在类似微生物化石的事物（有争议）

2007年，加拿大发现的距今37.7亿年至42.8亿年的细菌化石

​ 若外星人与地球人长相相似，那么我们更有可能认为它们是外星人，但问题是我们无法衡量什么叫相似。另外，如果外星人在表象上与我们大相径庭呢？因此，作者试图寻找某些数学性质在底层起作用，用于衡量“生命”。

宇宙信息理想实验

​ 假设我们接收到宇宙中的一段字符ACXLGICXGOXEMZBRCNKXACXLPICXEMZBRCNKX，那么该字符是否包含了某种信息？通过搜索字符串的重复结构，我们发现EMZBRCNKX 出现了 2 次，而在短文本中完全随机出现这么长的相同字符串2次概率是极低的，因此我们就有一定依据认为这段字符串存在一定语义。ACX也出现了两次，那么它可能也意味着什么。而其他没有重复出现的字符串，我们还不能明确它们是否存在含义，但如果它们在其他语料中出现，那么它们应该也具有语义。

​ 事实上，这段字符串是“we live in Jupiter, we love Jupiter”经过变换获取的。

推导梯径

​ 假设利用包含A、B、C、D、E、F的集合，获取特定字符串$\mathcal{X}=ABCDBCDBCDCDEFEF$的最快方式是什么？

​ 首先，定义一个基础集$S_0={A(0),B(0),C(0),D(0),E(0),F(0)}$，作为一个特殊的“偏序多重集”。

• 基础集元素是“偏序”的（有序的部分用”//”隔开，”//”之间称为一层，无序的部分用“，”隔开）
• 元素后括号内记录元素的个数（“重数”）
• 基础集的元素都成为“组件”
• 待生成的字符串$\mathcal{X}$为“目标组件”
• “生产操作”指取偏序多重集中的若干组件（也可取重数为0的组件），对应重数相应减少，再以某种形式结合在一起，生产新的组件放入集中抽取组件最高层的下一层，进而产生了一个新的偏序多重集

​ 因此，生成目标组件$\mathcal{X}$的一种路径

梯径：对于一条路径$S_0\to S_1 \to…\to S_n\Rightarrow\mathcal{X}$，取最终集合$S_n$，删去所有重数为0的元素，将所有负重数取绝对值作为对应组件重数，并保留所有偏序不变，获取另一偏序多重集$J$即为目标组件$\mathcal{X}$的梯径，梯径中的组件称为“梯元”。

​ 例1的梯径为$J_{\mathcal{X},1}={A,B,C,D,E,F//CD,EF//BCD(2)}$，重数为1时省略重数。

​ 一条路径对应一条梯径，但一条梯径可以对应多个路径。此外，任意组件都有至少一条“平凡梯径”，即完全有基础组件作为梯元的梯径。

定义梯径的目的是过滤掉生成目标组件过程中冗余步骤信息。

• 梯元是被重复利用的组件，因此最终获取目标组件的过程能被简化
• 对任一梯径$J_\mathcal{X}$，$N_a =\sum\limits_{i\in J_\mathcal{X}}(m_i\times n_{i,a})$对每个字符都成立
  • $N_a$为目标组件$\mathcal{X}$中字符$a$出现的次数
  • $i$为该梯径$J_\mathcal{X}$中的梯元
  • $m_i$是梯元$i$的重数
  • $n_{i,a}$为梯元$i$中字符$a$出现的次数

​ 梯图表示

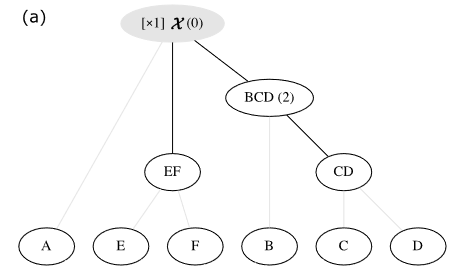
• 梯径的单位长度：任意2个组件并排在一起的一次操作
  • 一单位长度成为1程
  • 生成操作实际上是将$n$个组件并排，故对应$(n-1)$程
• 梯径$J$的长度：梯径中所有生成操作的长度和$|J|$
  • 用于衡量生成目标组价花费的代价
• 目标组价$\mathcal{X}$的梯径度$\lambda(\mathcal{X})$：$\mathcal{X}$的最短梯径的长度。单位为“程”
• （组价、目标组价、梯元的）规模度$S(i)$：最短平凡梯径长度
• 目标组价$\mathcal{X}$的有序度：$w(\mathcal{X})=S(\mathcal{X})-\lambda(\mathcal{X})$
  • 衡量通过组价结合节约的步骤和代价
• 任一梯径$J_\mathcal{X}$的长度可直接由它的偏序多重集表示算出，无需转化为对应路径
  • $|J_\mathcal{X}|=S(\mathcal{X})-\sum\limits_{i\in J_\mathcal{X}}m_i\cdot (S(i)-1)$
    • $S(\mathcal{X})$为目标组价$\mathcal{X}$的规模度
    • $S(i)$为梯元$i$的规模度
    • $m_i$为梯元$i$的重数
    • $i$为梯径$J_\mathcal{X}$的梯元
• 目标组价$\mathcal{X}$的有序度$w(\mathcal{X})=\sum\limits_{i\in J_\mathcal{X}}m_i\cdot (S(i)-1)$
• $\lambda(\mathcal{X})+w(\mathcal{X})\equiv S(\mathcal{X})$

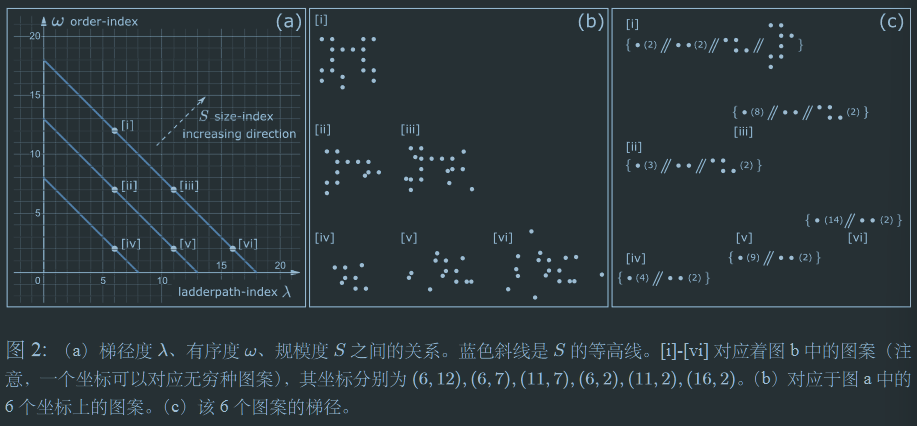
梯径度和有序度为复杂性的两个轴

​ 梯径度衡量了系统$\mathcal{X}$的复杂性，蕴含了信息量的全部知识。

​ 有序度描述了有多少冗余信息可以被组价节约。

相同梯径度下，一个系统越有序，则它的规模越大；相同的规模下，一个系统越有序，则它的梯径度越小，即蕴含的信息越少，构造难度小

最短梯径的算法

• 创建空的多重集$\mathcal{H}$用以存放组价
• 从目标系统$Q$出发，每个不同的组价只保存一个在$Q$中，重复组价放入$\mathcal{H}$中
• 以预设的方式持续切割$Q$中组件，并对切割后的$Q$重复上一操作
  • 优先寻找最长的重复子字符串
• 重复上一步骤，直至$Q$中不能找到重复的字符串或字符，并将剩余字符串全部切割为基础组件，放入$\mathcal{H}$中，此时$\mathcal{H}$记录了一条梯径
• 将$\mathcal{H}$中字符串的层次关系排列清楚，得到梯径的偏序多重集表示
• 遍历所有切割方法，即可找到所有可能梯径，进而获取最短梯径

​ 当系统非常复杂时，即使不能获取严格最短的梯径，但往往足够短。

遗憾的是作者没有提供证明，我没有想清楚如何保证

梯径系统

• 能够生成新组件
• 部分或所有组价可复制

​ 梯径系统意味着梯径度$\lambda$与系统的生成概率成反比。

​ 至此，我们就可以回到我们最初探讨的生命问题了。作者认为生命得以起源并非是某种奇迹，而是通过“梯径机制”。但在这之前，我们先探讨一个关于语言的例子。

外星信号（孤立体系）

​ 假设收到外星信号字符串$\mathcal{y}=TBCDEFRBCDEFTEFHKREFHJKLMUVTEFPSMU$，判断是否包含信息。由于是孤立体系，所有没有其他信息可以与$\mathcal{y}$一起被考虑。

​ 依据梯径理论，字符串组织得比较有序。事实上这句话指：“my mother made a chocolate cake your mother made a chocolate cake my chocolate cake was delicious your chocolate cake was not delicious I ate half of my chocolate cake and you ate half”，这里$\mathcal{y}$中每个字符代表一个单词。

​ 但这里面仍然存在一些问题

• $\mathcal{y}$本身没有包含语句的具体信息，只包含了句子各部分之间的关系，若没有其他渠道信息，我们永远无法破解$\mathcal{y}$的内容（如古老语言失传）
• 多次出现的片段包含了很多冗余信息
• 无法判断非重复字符是否包含信息
• 我们把字符看做基本信息单元，但事实上没有充足理由这么做（排除先验知识）
  • 定义基础集是一个相对主观的过程

人类语言（联合体系）

​ 如果我们收到很多信号，应该分析整个体系的梯径。

​ 若将$\mathcal{y}$视作孤立体系，很有可能导致错误的或者过度外推的结论。

生命起源

​ 基于梯径理论，作者批驳了著名的“垃圾场龙卷风”理论。“垃圾场龙卷风”理论假设了制造飞机的困难度在于使用最基本的零构件组装飞机，但梯径理论并不这么看，如果将问题简化为使用发动机、机翼、控制电路等组件构建飞机，那么生命产生的难度将极大降低，远比想象的简单。

​ 在梯径系统中，每生成一个新梯元，整个系统的梯径度就增加了，即心痛蕴含的信息量增加了；每复制一个梯元，整个系统的有序度就增加了，所以梯径系统的梯径度和有序度会自然增加，朝着复杂方向演化。（这个说法草率了）

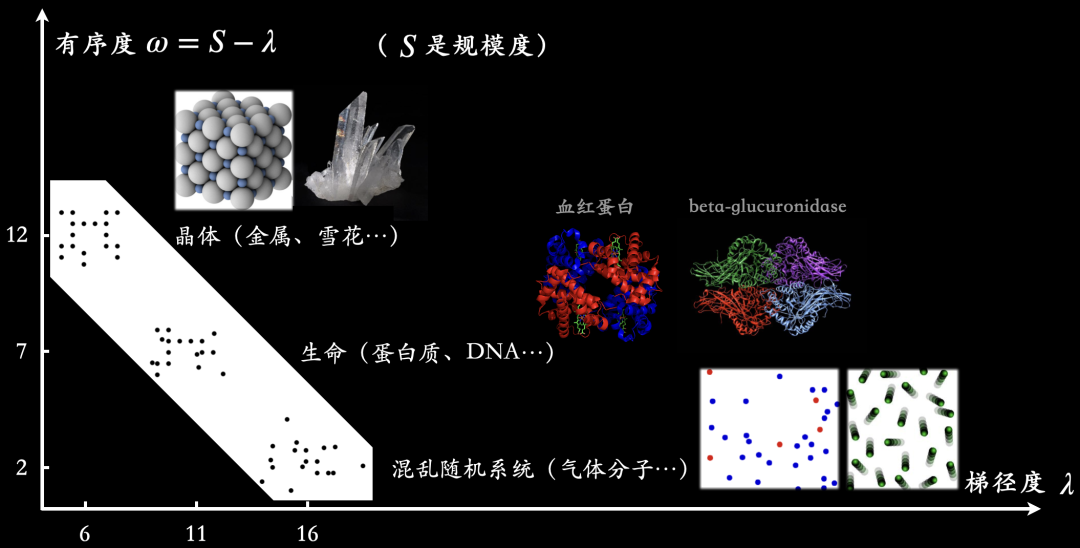
​ 因此，相较于高梯径度、低有序度的混乱气体分子和低梯径度、高有序度的晶体而言，梯径度和有序度都处于较高水平的物质更有可能被称之为生命。

---

---

• Previous
  【阅】本周阅读摘选2023-01-30 → 2023-02-05
• Next
  【阅】本周阅读摘选2023-02-13 → 2023-02-19

---