学术相关
通过AI聊天机器人测量个性,靠谱吗?1
传统的个性测量手段通常被批判在效标关联效度上较弱;难以应对伪装或相应失真情况;由于个体差异,题项在行为跨情境一致性上存在解释特异性;测验冗长。而相较于传统的个性测量手段,基于AI的个性测量在技术、数据收集(数字足迹)和算法上都有其独特优势,对上述问题有更好地处理。
在前人文献批评中,作者指出早期的AI个性测量需要使用个人敏感信息(社交账号等),通常在实际应用中受到政策限制或触发隐私担忧,因此现在AI个性测量应更多地采用视频交流和文字交流的形式。此外,目前学界缺少对机器推断个性得分的心理属性进行检验,前人仅仅对问卷评分和机器推断进行了比对。所以,作者进一步地检验了机器推断个性评分的信效度。
| DV | 控制变量 | IV | |
|---|---|---|---|
| 推断模型构建 | 自我报告大五得分 (30个维度) | 机器推断大五得分 | |
| 主实验 | GPA peer-rated college adjustment |
ACT(SAT转化) 自我报告大五得分 |
机器推断大五得分 |
简易总结:作者对大五模型的测量形式做了创新,并进行信效度检验。结果表明:作者构建的测量模型在结构效度表现良好,具有较好的聚合效度,而区分效度和效标效度上与自我回报大五人格测量量表表现类似,均不佳。
样本真实标签采用自我报告的问卷个性测量得分。
数据限制了学习器的能力; 打破传统方法缺点的命题不成立可选对话机器人平台:IBM Watson Assistant、Google Dialogflow、Microsoft Power Virtual Agents、Juji’s AI chatbot
Juji平台提供了无代码、脚本、API三种免费调用方式
作用:建议情感评论 & 控制偏题
作者没有交代Chatbot问题的生成方式和设计逻辑
分析指标
- 实质效度Substantive Validity(内容效度Content validity)
- ML的黑箱特征导致内容效度检验困难
-
间接检验:Park et al.’s (2015)
-
n-grams频率统计
-
分析n-grams与已知目标维度语句特征的相关性
-
类似点互信息算法PMI?
-
-
- ML的黑箱特征导致内容效度检验困难
- 结构效度Structural Validity
- 可靠性Reliability
- 内部一致性:在人格域层次使用Cronbach‘s α
- 重测信度:直接计算
- 折半信度
- 将参与者提供的语料随机切分为近似相等的两部分
- 使用模型对两份语料进行分别预测
- 计算两组得分的相关性并进行Spearman-Brown校正
- 普适性Generalizability
- 模型应用在不同文本时能否返回相近的个性得分
- 因子效度Factorial validity
- 机器推断个性的方面得分可以还原大五得分结构时成立
- 可靠性Reliability
- 外部效度
- 聚合效度
- 比较了同一特征机器推断和问卷个性得分的相关度
- 区分效度
- 使用multi-trait multi-method(MTMM)矩阵检验
- 前人研究的ML模型区分效度较差
- 效标效度
- 前人研究表明,已有测量模型的效标效度较弱
- ML推断与自我报告人格得分关联较弱(.20-.40)
- 自我报告人格得分与工作表现关联较弱(0.18)
- 理论预期ML推断与校标关联很弱(0.3×0.18)
- 前人研究表明,已有测量模型的效标效度较弱
- 聚合效度
研究方法
研究设计符合the Journal of Applied Psychology method checklist,开放于OSF。(作者声称原始数据和程序代码存在版权限制,未公开)
- 样本
- 1957名心理学课堂的本科生
- 采用SONA系统的对象池
- 训练集(n=1037)
- 2018年~2020年:lab+online[2019 & 2020]
- 1477被试中有1037人拥有匹配的人格测试和AI对话
- 训练集不收集criteria data (GPA & peer-rated college adjustment )
- 测试集(n=407)
- 2017年:lab
- 设计样本量480,73人退出
- 379人报告了ACT(SAT-转化)成绩,301人得到同窗评价
- 1957名心理学课堂的本科生
- 采集程序
- Qualtrics公司线上大五人格测量IPIP-300
- AI聊天平台 20~30min
- 一系列开放式问题
- SAT/ACT、GPA
- 提供3个大学同窗的年龄和邮箱地址
- 实验完成后,立即随机发邮件邀请一个同窗进行同窗评估
- 一周后发送提醒邮件
- 若无回应则随机邀请其他同窗
- 直至得到回应或3个同窗全部用尽
- 为同窗通过$5报酬
- 实验完成后,立即随机发邮件邀请一个同窗进行同窗评估
- 重测信度
- 单独邀请74名本科生进行AI对话重测,间隔3~35天
- 测量
- 自我报告人格问卷:IPIP-300
- 包含30个维度
- 机器推断人格
- 30个维度
- 每个方向得分基于维度平均值
- 作者也基于自我报告的维度和方向得分建立了机器学习模型
- 结果表明两种方法结论近似
- 客观校园表现:累积GPA
- 同窗评价调整:Oswald et al 12项行为锚定评分量表BARS
- 12个因子得分累加作为总分
- 与GPA相关度0.21
- 控制变量
- ACT/SAT分数
- 自我报告人格问卷:IPIP-300
- 自然语言处理
- 使用Universal Sentence Encoder对句子进行编码
- 建模
- Elastic net regression
- L1和L2正则加权
- 探索性结构方程模型Set-ESEM
- 平衡拟合优度和简约型
- Elastic net regression
- 评估
- Tucker’s Congruence Coefficient (TCCs)
- 量化评估两个量表(自我报告&机器推断)的相似度
- MTMM矩阵评估聚合效度和区分效度
- 效标关联效度
- 回归分析
- Tucker’s Congruence Coefficient (TCCs)
实验结果
ML模型较好的还原了大五的结构,因子载荷与自我报告模型近似。ML模型具有较好的聚合效度,但在区分效度上表现较弱,且存在较高的共同方法偏差。
在效标效度上,控制了ACT得分后的GPA和同窗评价调整都显著的与部分机器推断属性关联,符合前人实验预期。通过10组(5个领域×2个效标)分层回归分析机器推断领域得分的增量效度。控制了ACT得分后自我报告人格领域得分展示了温和的增量效度。同时控制ACT得分和自我报告人格领域得分,机器推断人格得分没有解释GPA和同窗评价的额外方差。总体上,机器推断人格得分和自我报告人格得分相比,具有略低的效标效度,但少量领域可能存在轻微的增益。
稳健性检验
- 若参与者提供更少的输入,机器推断人格分数的可靠性和有效性是否会受到影响?
- 实验组拆分:全样本组;最短输入$\frac{1}{3}$组;较长输入$\frac{2}{3}$组
- 可靠性和有效性无显著差异
- 实验组拆分:全样本组;最短输入$\frac{1}{3}$组;较长输入$\frac{2}{3}$组
讨论
- 重测信度
- 文本大小可能影响
- 使用两次相同任务产生$实验\times 参与者$交互相应
- 效标效度
- 虽然表现不佳,但大多数领域的相关系数落入自我报告大五模型的META分析区间内
在灾难期间使用社交媒体进行子事件检测2
我猜测可以被迁移到推广事件分析任务中。
文章有一些小问题。
使用社交媒体内容分析灾难问题并非一个新鲜问题,但作者认为前人的研究过于关于高层级灾难的分析,而忽视了影响小社群的小规模灾难衍生事件(sub-event)。实际上,灾难衍生出一系列小规模紧急事件,如亲属被困、电力短缺、建筑物损毁等地区性或小群体性问题的情境更为常见和重要,同时也是常常被忽视的环节。
本文致力于解决在灾难期间的子事件识别问题,提出了基于社交媒体的SEDOM-DD(Sub-Events Detection on sOcial Media During Disaster)模型。具体而言,重点解决1. 推文与灾难事件相关性识别任务 2. 灾难区域子事件发现任务。区别与其他技术,SEDOM-DD模型旨在识别灾难的次生效应,因此可以集成在现有的灾难系统中进行协作,从而更好地进行应急响应。
文献综述
- 有监督方法
- 加权图模型、TF-IDF、神经网络模型
- 问题:很多事件的模型训练成本高,结果获取效率低
- 无监督方法
- 基于聚类算法和相似性度量
- LDA、HDP、ILP
- 余弦相似度
- 基于聚类算法和相似性度量
- SEMOD-DD模型区别于前人模型
- 采用尽可能多的社交媒体信息
- 空间聚类算法
建模思路
- 数据收集
- 给定灾难事件及其影响范围
- 通过关键词或IP地址产查询posts
- 推文筛选
- 采用有监督机器学习技术识别关联推文
- 保留灾难相关推文和受灾区域用户推文
- 通用推文:提及灾难事件,但不包含次生灾害
- 非通用推文:提及次生灾害
- 推文富集
- 基于推文信息为无地理标签的推文估算坐标
- 使用地理编码网络服务检索当地PoIs及其常用指代名称
- 从文本中提取街道和地区名称(基于CoreNPL的实体识别分离地点名称)
- 构建PoI,街道,地区或城市四个精度级别的坐标
- 若推文提及街道或地区却没有PoI则随机在街道/地区内选取发生点
- 若推文仅提及城市则放置在城市等级
- 基于推文信息为无地理标签的推文估算坐标
- 子事件识别
- 利用空间的聚类算法识别子事件发生区域
- DBSCAN:最常用、抗噪声、数据和聚类大小灵活
- 文本分析标注子事件类别
- 在聚类中提取关键词和频率
- 基于频率排序
- 按频率与人工构建的子事件词典(含同义词)比对
- 利用空间的聚类算法识别子事件发生区域
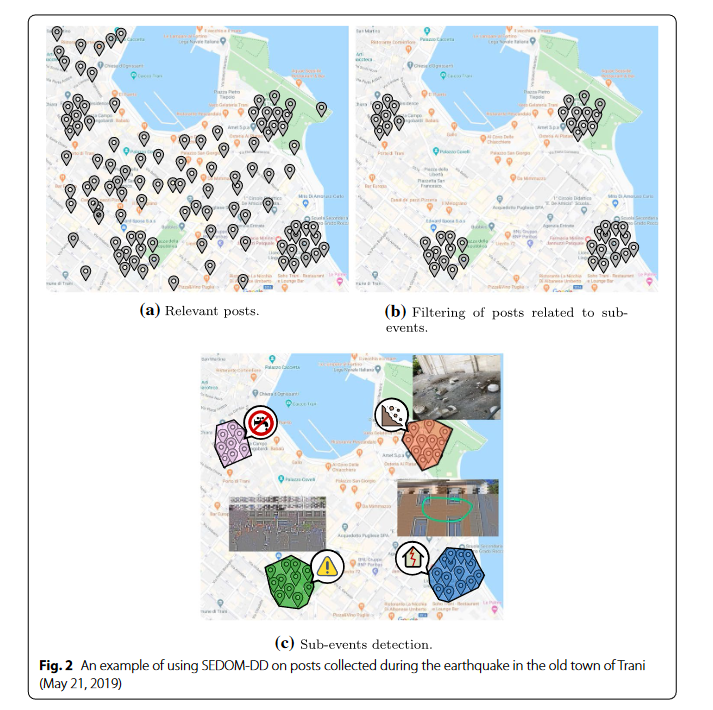
实验估算
- 数据收集
- 2009-2019年Twitter真实灾难事件数据集
- 地震、洪水、飓风
- Twitter提供下载特定主题用户推文的公共APIs
- 基于真实事件的合成数据集
- 2009-2019年Twitter真实灾难事件数据集
- 推文筛选
- 构建人工分类数据集$D_1$:包含5000推文;一半与灾难相关,一半无关
- 测试算法
- 朴素贝叶斯、KNN、SVM、逻辑回归、决策树、随机森林、XGBOOST(bi-gram)
- 神经网络(Word2vec+CNN)
- 令$P={p_1,p_2,..,p_n}$为发布于灾难事件$E$之后的推文集,$p_i$包含属性:
- $user_{id}$:发文用户
- $timestamp$:时间戳
- $text$:$p_i$文本
- $tags$:$p_i$标签
- $coordinates$:$p_i$坐标/undefined
- $profile_{geo}$:$p_i$发文用户个人资料的地理信息
- $length$:$p_i$文本信息
- $numKeywords$:$p_i$文本中包含的灾难相关关键词数量
- 分类标签:相关/无关
- 不平衡数据,需要数据平衡
- 所有算法的分类表现均较好
- 神经网络模型最好(80%+)
- 合成数据集子事件检测
- 通过真实社交媒体推文构建多个不同类型和精度级别的推文数据集
- 合成数据集生成
- 仿真参数
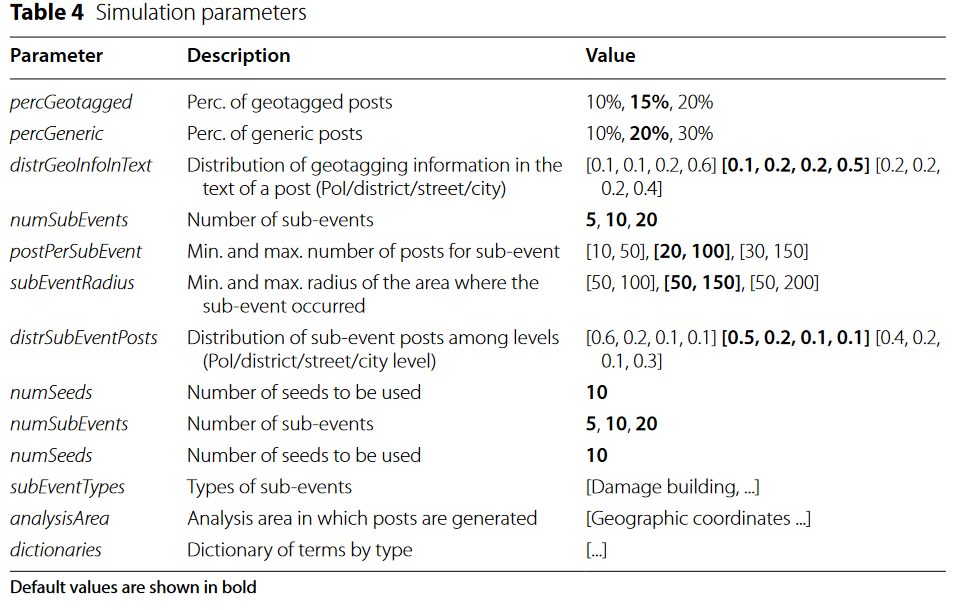
- 生成算法伪代码

- 仿真参数
- 子事件检测
- 伪代码(推文富集lines 1-11)

- 伪代码(推文富集lines 1-11)
- 实验结果
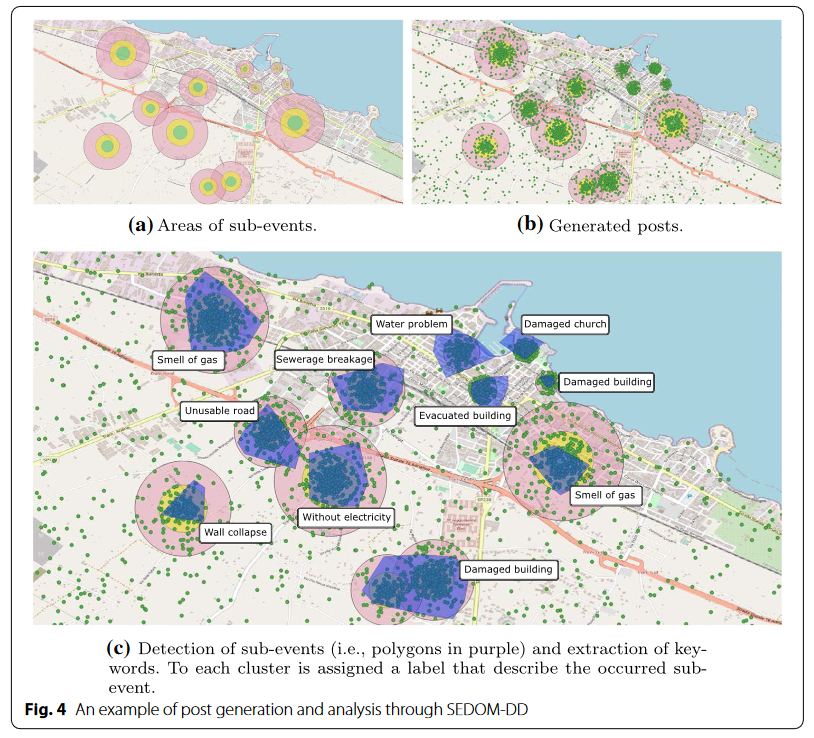
- PoI-绿色;街道-黄色;地区-粉色;城市-无
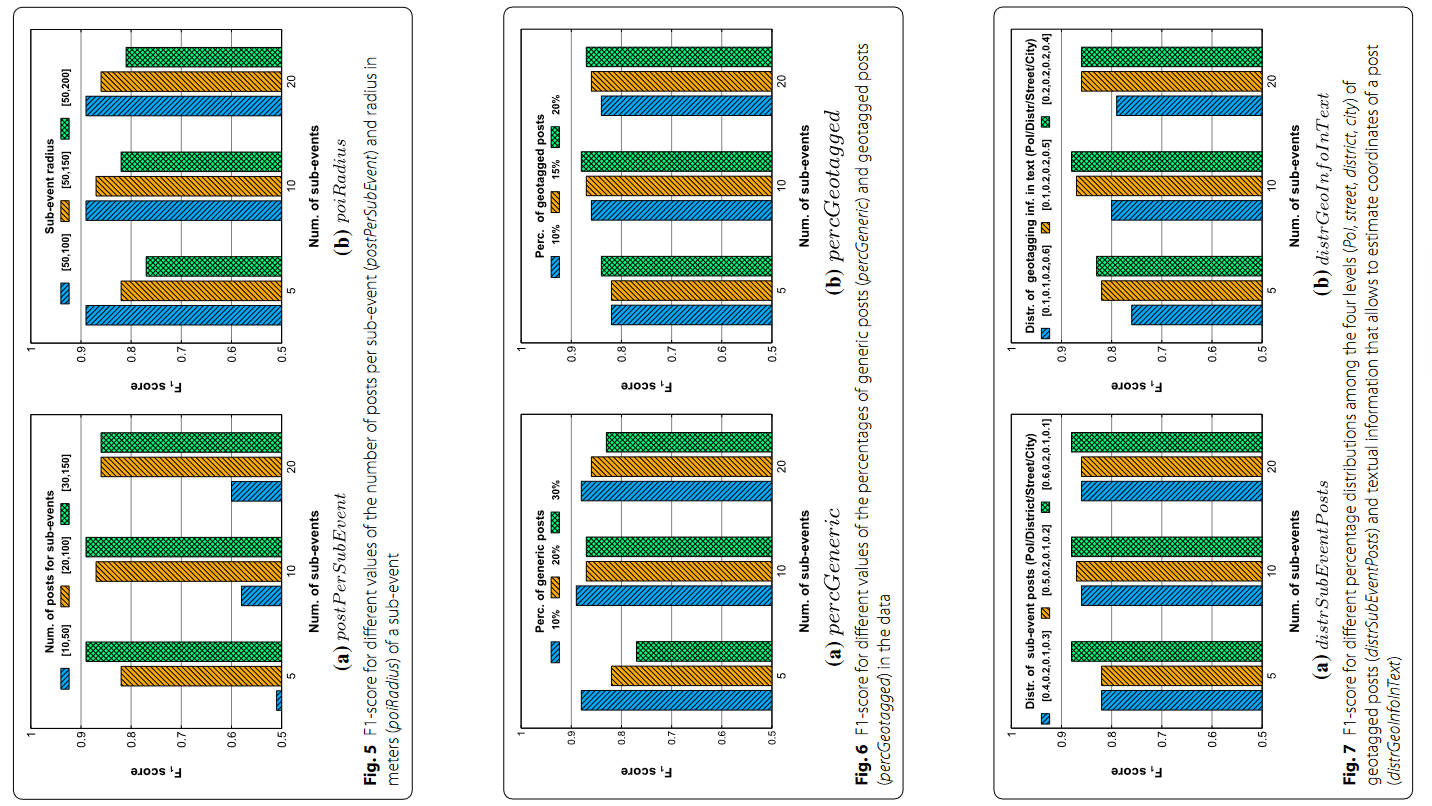
- 数据富集环境极大地提升了模型的准确度(大大增强可用数据)
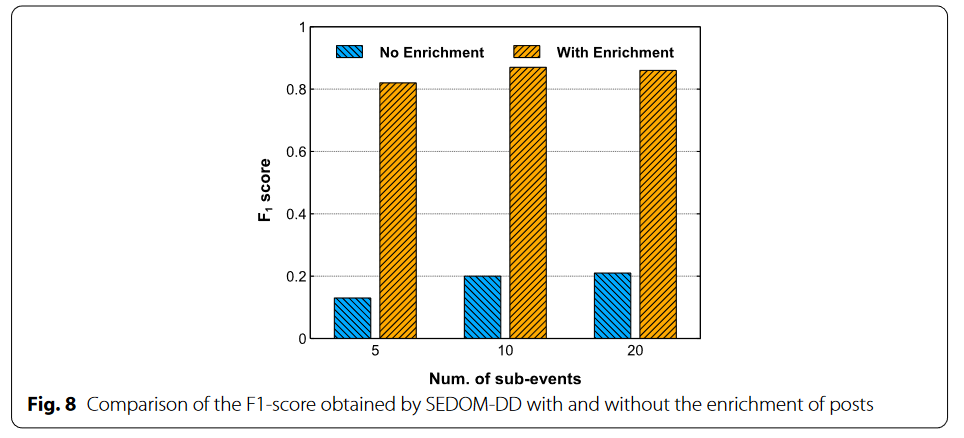
- 真实世界数据集
- Hurricane Harvey, Texas, 2017
- 29%相关;1%带地理标签;富集后15%推文可识别
- 2%携带子事件
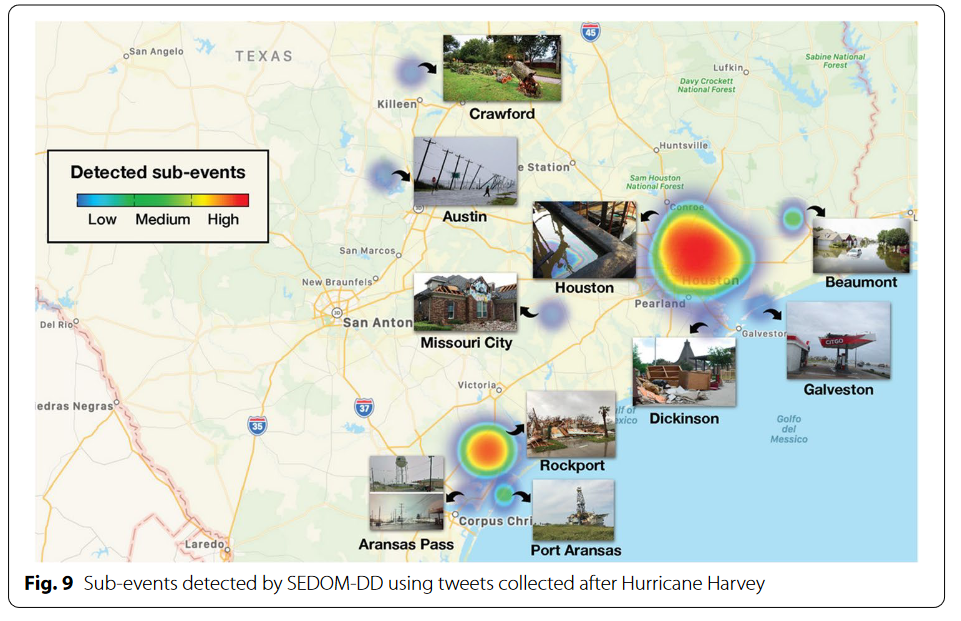
- 由于工作量过大,显然作者没有真实数据的ground truth
- 但已有研究表明ChatGPT在数据标注上有较好的表现
- Hurricane Harvey, Texas, 2017
毛咕噜TOP5: AI自动智能化给普通劳动者的灾难性影响已经发生!3
引言
自1980年以来的40年里,收入不平等问题在美国急剧恶化。拥有研究生学位者的真实工资增长的同时,低教育水平工人的真实收入下降或停滞。本文理论指出,由于技术的自动化取代了工人过去所从事的工作,导致了对低技能工人需求的转变。本文主要量化了自动化在工资不平等问题上的效应,分析表明美国过去40年里整体工资结构变化的50%~70%可以归结为自动化的影响,自动化降低了从事常规任务的工人薪资,而从事未被自动化替代工作的人享受着薪资增长。
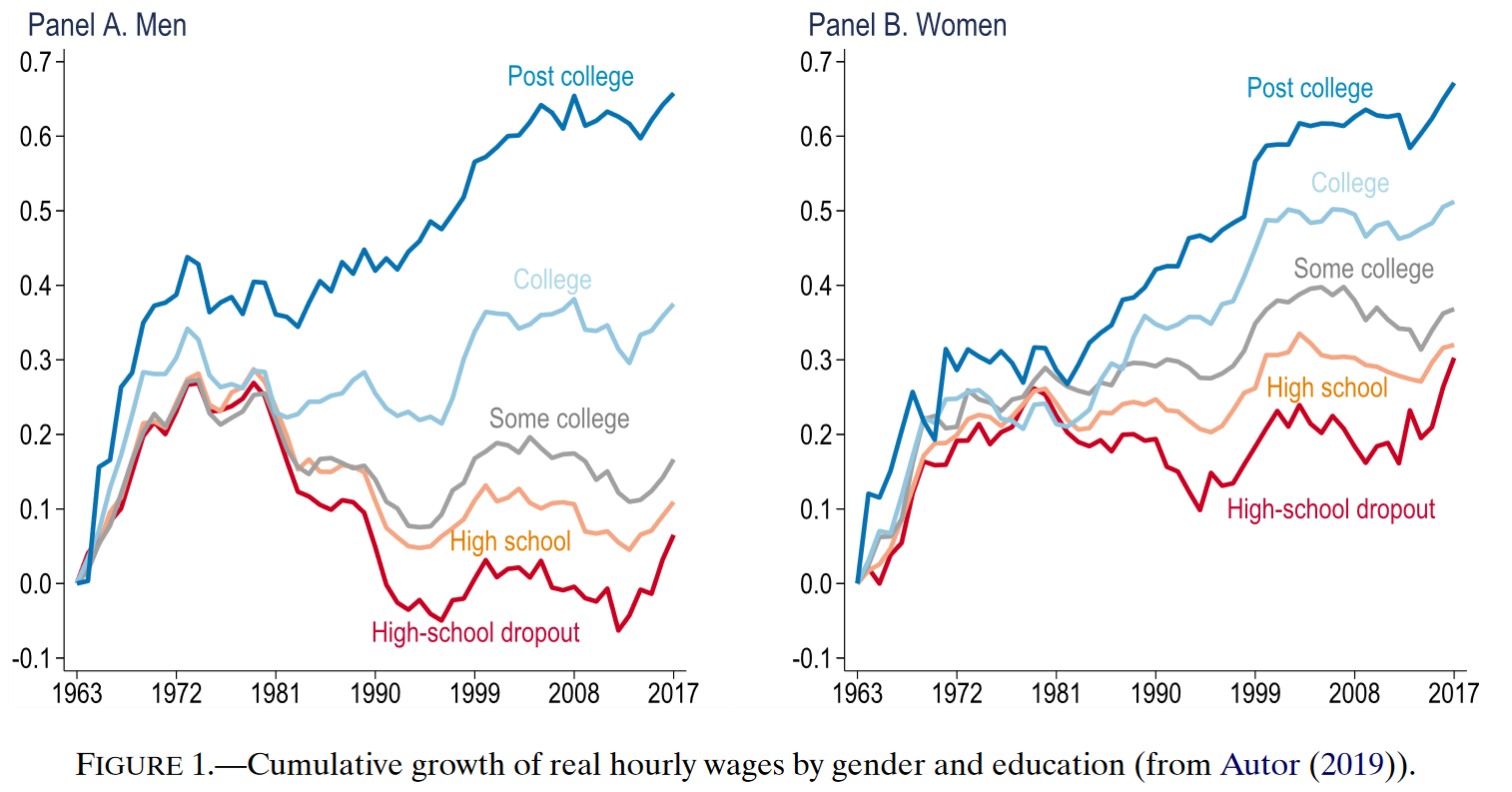
技术进步可以增加一部分群体(高知)和现有任务中资本的产出;同时,由于自动化,部分原来分配给工人的任务被转向分配给资本,扩大了资本的任务范围。作者的模型澄清了技术变革的不同影响:自动化将工人从原有比较优势的任务中置换出来,进而降低了他们的相对工资,甚至是实际工资;而直接提高高技术劳动力生产力的技术不会导致工作分配偏移,并且总是增加非技术工人的工资;此外,受替代弹性影响,这些技术变革的效应最终对不平等和要素份额的影响是不明确的。
本文验证了直接任务置换和工人的真实工资之间存在稳健的负相关。作者通过机器人、专业软件、专业及其设备的使用率数据指示的自动化引发的劳动份额下降来衡量任务置换。这些数据解释了1987~2016年45%的工业劳动力份额下降。在回归分析中,直接任务置换解释了50-70%的1980年至2016年工资结构变化,且是稳健的。通过控制变量,作者证明了这一效应只与自动化有关,而非受其他形式的技术变革或资本深化。然而,在简化形式的分析中,生产力提升对工作的共同影响并入了截距项,因此结果对实际工资水平变化没有参考价值;自动化集中在部分行业,它改变了经济中的工业结构,进而转变了工人需求类型;简化形式分析集中在直接任务置换上,没有考虑涟漪效应。
本文的第三部分对一般均衡趋势进行量化分析,估计自动化对工资结构、实际工资、全要素生产率、产出、经济产业构成的全部影响。结果表明自动化解释了期间50%的工资结构变化和80%的大学溢价,同时,自动化极大地降低了低学历者收入水平,仅微小地增加了平均工资水平、GDP和TFP。
理论框架
单一部门模型
基于固定替代弹性生产函数构建$y=(\frac{1}{M}\int_{\tau}(M\cdot y(x))^{\frac{\lambda-1}{\lambda}}\cdot dx)^{\frac{\lambda}{\lambda-1}}$,总产出由$\tau$集合中大量任务$M$的产出组合而成,其中$x$表示任务索引,固定替代弹性$\lambda$。
每个任务可以通过资本或不同类型的劳动力$g\ (g\in \mathcal{G}={1,2,…,G})$进行产出:$y(x)=A_k\cdot\psi_k\cdot k(x)+\sum\limits_{g\in\mathcal{G}}A_g\cdot\psi_g(x)\cdot\mathscr{l}_g(x)$,其中$\mathscr{l}_g(x)$表示分配给任务$x$的$g$类劳动者总数,$k(x)$为分配给特定任务的资本总量,$A_k$、$A_g$为标准要素增强型技术。$\psi_k(x)$和${\psi_g(x)}_{g\in\mathcal{G}}$决定要素的比较优势和专业化模式。
特定任务资本$k(x)$由常数边际开销$\frac{1}{q(x)}$处最终产出决定,因此净产出,即消费$c=y-\int_{\tau}(k(x)/q(x))\cdot dx$。
劳动供给无弹性。
市场均衡被定义为使消费最大化的要素任务分配与资本品生产计划。给定劳动供给$\mathscr{l}=(\mathscr{l}_1,\mathscr{l}_2,…,\mathscr{l}_G)$,市场均衡由工资$w=(w_1,w_2,…,w_G)$、资本生产决策$k(x)$、劳动力任务分配$\mathscr{l}_g(x)$决定,使得要素任务分配开销最小化、资本生产决策最大化净产出、资本品和不同类型劳动市场出清。$w_g$对应实际工作。
【打破僵局规则】:作者假定当任务可以被相同成本的不同要素组合生产时,优先分配给索引更高的资本或劳动,同时假设每项要素在一些任务上都有严格比较优势。
成本最小化和打破僵局规则决定了每项任务使用单一要素进行生产,令$\tau_g$表示分配给$g$型劳动力的任务,$\tau_k$表示分配给资本的任务,可以推导出:
$\begin{aligned}\tau_g=&{x:\frac{w_g}{\psi_g(x)\cdot A_g}\leq\frac{w_j}{\psi_j(x)\cdot A_j}for\ j<g\&\frac{w_g}{\psi_g(x)\cdot A_g}<\frac{w_j}{\psi_j(x)\cdot A_j} for \ j>g\& \frac{w_g}{\psi_g\cdot A_g}<\frac{\frac{1}{q(x)}}{\psi_k(x)\cdot A_k}}\end{aligned}$
$\tau_k={x:\frac{\frac{1}{q(x)}}{\psi_k(x)\cdot A_k}\leq\frac{w_j}{\psi_j(x)\cdot A_j)}for\ all\ j}$
给定要素的任务分配,定义$g$类劳动力和资本的任务份额$\Gamma_g(w,\Psi)=\frac{1}{M}\int_{\tau_g}\psi_g(x)^{\lambda-1}dx,\ \Gamma_k(w,\Psi)=\frac{1}{M}\int_{\tau_k}(\psi_k(x)\cdot q(x))^{\lambda-1}dx$用来衡量一组任务根据任务重要性权重分配给一个要素。
-
命题1—均衡:存在一个独特的均衡,此处产出、工资、GDP中资本份额($s^K$)可以表示为任务份额的函数:
$y=(1-A_k^{\lambda-1}\cdot\Gamma_k)^{\frac{\lambda}{1-\lambda}}\cdot (\sum\limits_{g\in\mathcal{G}}\Gamma^{\frac{1}{\lambda}}_g\cdot(A_g\cdot\mathscr{l}_g)^{\frac{\lambda-1}{\lambda}})^{\frac{\lambda}{\lambda-1}}$
$w_g=(\frac{y}{\mathscr{l}_g})^{\frac{1}{\lambda}}\cdot A_g^{\frac{\lambda-1}{\lambda}}\cdot\Gamma_g^{\frac{1}{\lambda}}\ for\ all\ g\in\mathcal{G}$
$s^K=A_k^{\lambda-1}\cdot\Gamma_k$
与标准CES生产函数相比,该函数任务份额是内生的,$\Gamma_g$不仅与要素价格相关且与技术相关;要素间替代弹性$\sigma\geq\lambda$,受任务重新分配的内生影响;$1-A_k^{\lambda-1}\cdot\Gamma_k>0$反映了生产的迂回性。
真实工资的等式是直觉的。真实工资由每类劳动力的边际产出给定,即每位工人(上升至$\frac{1}{\lambda}$次方)和要素扩张型技术$A_g$(上升至$1-\frac{1}{\lambda}$次方)的函数。同时,工资也依赖于任务份额$\Gamma_g$ ,强调本模型的关键点:要素的真实工资与其任务份额关联。
自动化通过重分配任务份额,降低劳动力任务份额影响均衡价格和数量。
自动化指通过增加在原分配给劳动力的任务中资本的生产率(或降低生产资本的消耗),导致劳动力在该任务中被置换。外包同样导致了劳动力被置换,因此可以被纳入到该分析框架中。
作者将自动化建模为使资本生产效率增长,最终在原先分配给劳动力的任务集中的一个无穷小子集任务($\mathcal{D}_g\subseteq\mathcal{T}_g$)上超越劳动力。自动化对劳动力群体$g$的直接任务替代效应$d\ ln\ \Gamma_g^{auto}=\frac{\frac{1}{M}\int_{D_g}\psi_g(x)^{\lambda-1}dx}{\frac{1}{M}\int_{\tau_g}\psi_g(x)^{\lambda-1}dx}$只取决于自动化技术带来的潜在改进(不包含任务跨要素的重新分配);自动化带来的成本缩减效应$\pi_g=\frac{\frac{1}{M}\int_{D_g}\psi_g(x)^{\lambda-1}\cdot\pi_g(x)dx}{\frac{1}{M}\int_{D_g}\psi_g(x)^{\lambda-1}dx}$,其中$\pi_g(x)$为自动化任务$x\in\mathcal{D}_g$带来的成本节约。
作者通过2个假设排除涟漪效应。
假设1.1:劳动力只能生产单一任务$\psi_g(x)>0\ only\ if\ \psi_{g’}(x)=0\ for\ all\ g’\neq g$
假设1.2:$\psi_k(x)>\underline{\psi}$且$q(x)>\bar{q}$对所有$x\in S={x:\psi_k(x)>0}$成立,其中常数$\underline{\psi}$和$\bar{q}$满足$\mathcal{T}_k=S$
假设2确保了当资本生产率足够高且开销足够低的时候,所有的任务都会被分配给资本。
-
命题2—科技的比较静态分析:科技变化(要素增加、生产力深化、自动化)对真实工资、全要素生产率、产出和资本份额的影响
$d\ ln\ w_g=\frac{1}{\lambda}d\ ln\ y+\frac{\lambda-1}{\lambda}d\ ln\ \tilde{A}_g-\frac{1}{\lambda}d\ ln\ \Gamma_g^{auto}$,
$d\ ln\ y=\frac{1}{1-s^K}\cdot(d\ ln\ tfp+s^K\cdot d\ ln\ s^K)$,
$d\ ln\ tfp=\sum\limits_{g\in\mathcal{G}}s_g^L\cdot d\ ln\ \tilde{A_g}+s^K\cdot d\ ln\tilde{A}_k+\sum\limits_{g\in\mathcal{G}}s_g^L\cdot d\ ln\ \Gamma_g^{auto}\cdot \pi_g$,
$d\ ln\ s^K=(\lambda-1)\cdot ln\ \tilde{A}_k+\frac{1}{s^K}\cdot\sum\limits_{g\in\mathcal{G}}s_g^L\cdot d\ ln\ \Gamma_g^{auto}\cdot(1+(\lambda-1)\cdot\pi_g)$,
其中$d\ ln\ \tilde{A}_g=d\ ln\ A_g+d\ ln\ \Gamma_g^{deep}$,$d\ ln\ \tilde{A}_k=d\ ln\ A_k+d\ ln\ \Gamma_k^{deep}$,$s_g^L=w_g\cdot\frac{\mathscr{l}_g}{y}$为$g$组的GDP份额
要素增加和生产力深化技术使$g$组的真实工资因生产率($d\ ln\ y$)增长而提高,并通过$\frac{\lambda-1}{\lambda}\cdot d\ ln\tilde{A}_g$影响相对工资,相对工资是否提升取决于技术导致的生产效率提升和生产成本下降之间的博弈。当$\lambda>1$时,即为标准的SBTC文献的机制,技术增加$g$组的生产效率并提高其他工人的工资,因此基于技术的技术或资本-技术互补性的理论难以解释非技术工人的工资为什么会停滞或下降。
要素增加和生产力深化技术对于全要素生产率TFP的影响由$\sum\limits_{g\in\mathcal{G}}s^L_g\cdot d\ln\ \tilde{A}_g+s^K\cdot d\ ln\ \tilde{A}_k$,其逻辑是$g$组工人生产率提升1%,则整体TFP提升$s_g^L$%,资本生产率增加1%,TFP增加$s^K$%。
自动化对工资的影响为$\frac{1}{\lambda}d\ ln\ y-\frac{1}{\lambda}d\ ln\ \Gamma_g^{auto}$,该式第一项衡量了生产率效应,而第二项表明一组工人的真实工资变化依赖于他们受到的任务置换影响,该影响与替代弹性无关。
自动化对TFP的影响为$\sum\limits_{g\in\mathcal{G}}s_g^L\cdot d\ ln\ \Gamma_g^{auto}\cdot \pi_g$。若自动化带来的成本节约$\pi_g$是微小的,自动化会通过任务置换对工资结构产生可观的冲击,且只带来少量整体生产力提升。
自动化同时也会增加资本份额,降低劳动份额的附加值。
全模型:多部门模型
假设存在多个产业$i\in\mathcal{I}={1,2,…,I}$,产业$i$的产出由大小为$M_i$的任务集合$\mathcal{T}_i$使用CES生产函数聚合而成。
$y_i=A_i\cdot (\frac{1}{M_i}\int_{\tau_i}(M_i\cdot y(x))^{\frac{\lambda-1}{\lambda}}\cdot dx)^{\frac{\lambda}{\lambda-1}}$,$x$为任务索引,$A_i$为希克斯中性技术进步,$\tau_{gi}$表示产业$i$分配给$g$类劳动力的任务,$\tau_{ki}$为对应的资本分配。
产业级别的任务分配$\Gamma_{gi}(m,\Psi)=\frac{1}{M_i}\int_{\tau_{gi}}\psi_g(x)^{\lambda-1} dx,\Gamma_{k_i}(w,\Psi)=\frac{1}{M}\int_{\tau_{ki}}(\psi_k(x)\cdot q(x))^{\lambda-1}dx$
作者假设所有产业的输出以规模效用不变的方式整合为总产出$H(y_1,…,y_I)$,在文中采用隐含的指出份额$s_i^Y(p)$,其中$p=(p_1,…,p_I)$为产业价格。
-
命题3(命题1的多部门形式)—多部门均衡
$w_g=(\frac{y}{\mathscr{l}_g})^{\frac{1}{\lambda}}\cdot A_g^{\frac{\lambda-1}{\lambda}}\cdot (\sum\limits_{i\in\mathcal{I}}s_i^Y(p)\cdot(A_ip_i)^{\lambda-1}\cdot\Gamma_{gi})^{\frac{1}{\lambda}}$,
$p_i=\frac{1}{A_i}(A_k^{\lambda-1}\cdot\Gamma_{ki}+\sum\limits_{g\in\mathcal{G}}w_g^{1-\lambda}\cdot A_g^{\lambda-1}\cdot\Gamma_{gi})^{\frac{1}{1-\lambda}}$,
$1=\sum\limits_{i\in\mathcal{I}}s_i^Y(p))$
没有涟漪效应的工资方程
基于假设1,技术变革对工资的冲击可以被写成$d\ ln\ w_g=\frac{1}{\lambda}d\ ln\ y+\frac{1}{\lambda}\sum\limits_{i\in \mathcal{I}}w_g^i\cdot d\ ln\ \zeta_i+\frac{\lambda-1}{\lambda}d\ ln\tilde{A}_g-\frac{1}{\lambda}\sum\limits_{i\in\mathcal{I}}w_g^i\cdot d\ ln\ \Gamma_{gi}^{auto}$
其中,$d\ ln\tilde{A}_g=d\ lnA_g+\sum\limits_{i\in\mathcal{I}}w_g^i\cdot d\ ln\Gamma_{gi}^{deep}$,$d\ ln\zeta_i=d\ ln\ s_i^Y+(1-\lambda)\cdot(d\ ln\ p_i+d\ ln\ A_i)$,$w_g^i$表示$g$组在产业$i$中获得的收入份额,$\sum\limits_{i\in\mathcal{I}}w_g^i=1$。
在多部门的方程中,工资额外地受到技术转移改变产业组成的影响,方程通过$d\ ln\zeta_i$捕获这一现象。
实证分析
模型与数据联结
简化形式分析将工资方程中的$d\ ln\ y$纳入常数项;产业转移项$\sum\limits_{i\in \mathcal{I}}w_g^i\cdot d\ ln\ \zeta_i$通过$g$组劳动力对产业log附加值份额的影响确定参数;包含要素增加和生产力深化的$\frac{\lambda-1}{\lambda}d\ ln\tilde{A}_g$基于SBTC文献确定参数,作者假定$\frac{\lambda-1}{\lambda}d\ ln\tilde{A}_g=\alpha_{edu(g)}+\gamma_{gender(g)}+v_g$,其中$v_g$为额外的未察觉要素,教育和性别均以哑变量形式呈现。
模型的关键解释变量为$\sum\limits_{i\in \mathcal{I}}w_g^i\cdot d\ ln\ \zeta_i$。基于任务置换发生在可被自动化的任务上(作者使用常规任务具化)。
假设2:只有常规任务能够被自动化,且在一个产业内,不同类型的劳动力以一个相同的速率从常规任务中被置换。
此处分析假设$\lambda=1$,$Task\ displacement_g^{direct}=\sum\limits_{i\in\mathcal{I}}w_g^i\cdot\frac{w_{gi}^R}{w_i^R}\cdot(-d\ ln\ s_i^{L,auto})$
$w_g^i$为$g$类劳动力在产业$i$中获取的工资份额;$\frac{w_{gi}^R}{w_i^R}$参数化了$g$类劳动力在产业$i$中常规任务的专业化程度,该项可被自动化直接影响;在产业$i$中自动化引起的劳动力份额下降百分比为$-d\ ln\ s_i^{L,auto}$。作者使用两种方法测量最后一项,一种简便方式是将所有的劳动力份额下降归结于自动化,当$\lambda=1$时是有效的;另一种更倾向的方法是采用产业级别的自动化技术采用率分离自动化引起的产业劳动力份额下降。
数据、测量和描述性分析
- 49个产业1987~2016年BEA 综合工业水平生产账目(劳动力份额、要素价格和附加值)
- 1987~2016年间专用设备服务价值在附加值中的变化
- 1987~2016年间专业软件服务价值在附加值中的变化
- 1993~2014年间调整机器人渗透率
作者将1987年至2016年的行业(log)劳动力份额的变化与3个自动化技术的代用指标进行回归,并将自动化驱动的劳动力份额下降作为预测值计算。此外,作者通过中间产品进口变化代替外包进行分析。作者控制了总资本与附加值比率和产业全要素生产率、销售集中度、利润估计值、工会化率和中国进口竞争。
作者使用了人口普查和美国社区调查ACS数据衡量劳动力方面信息。
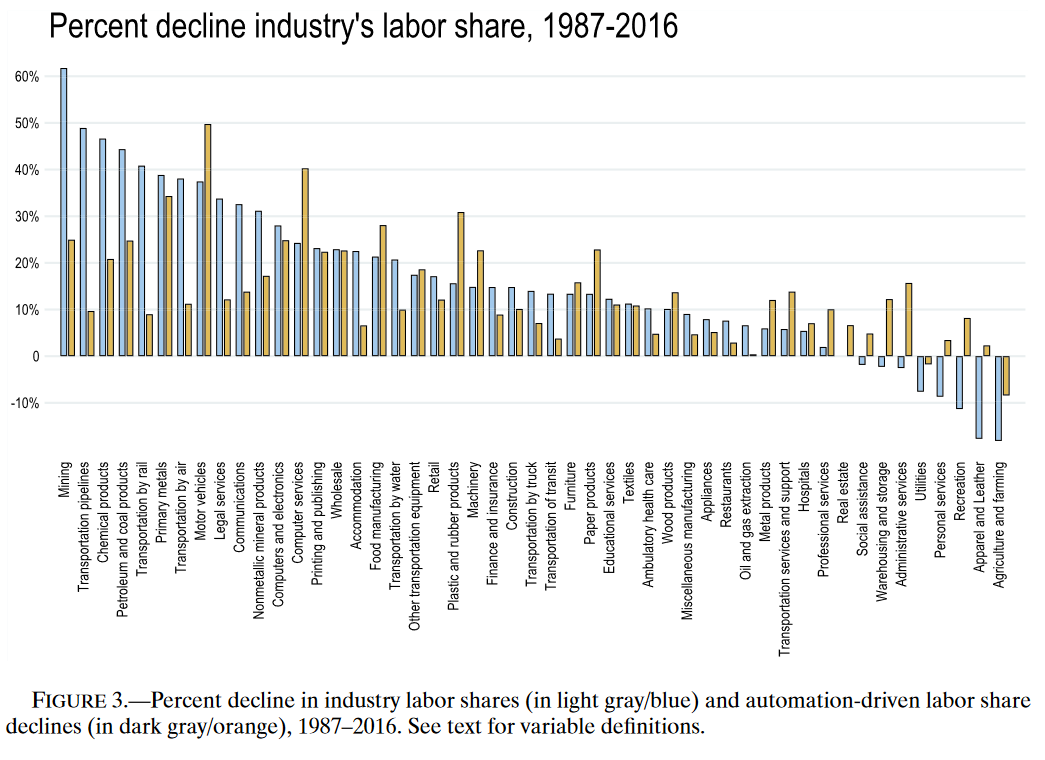
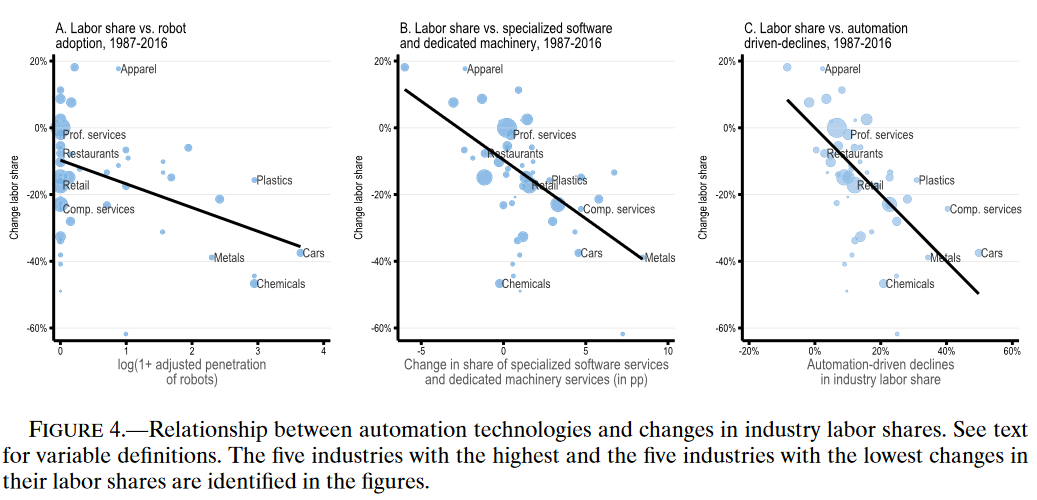
产业劳动力份额下降与自动化驱动劳动力份额下降有很强的相关性,表明劳动力份额下降最大的产业通常处于自动化技术采用的前沿。
自动化的三种替代共同解释了45%的产业劳动力份额变化方差。
人口统计群组中工作置换与工资关系
通过1980年人口普查(早于自动化技术主要突破)计算工资份额$w$。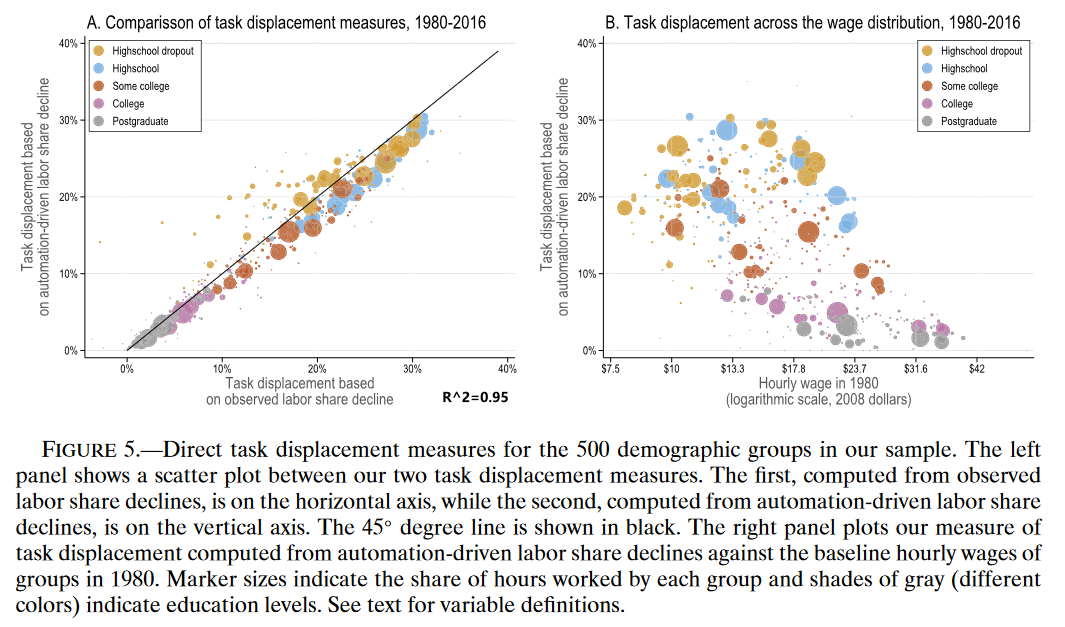
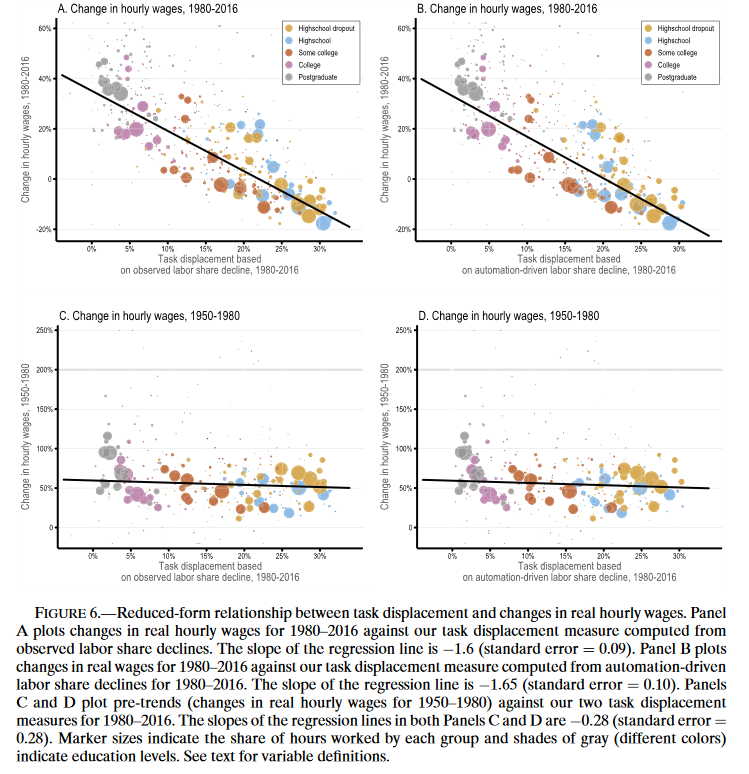
C、D两图证明了A、B描述的关系在1950~1980年期间不存在,所有类型工人拥有近似的稳健工资涨幅。
相关关系分析也指出低学历(无本科学历) 的工人的工作更容易被置换。
模型简化形式分析
基准模型
$\Delta ln\ w_g=\beta^d\cdot Task\ displacement_g^{direct}+\beta^s\cdot Industry\ shifters_g+\alpha_{edu(g)}+\gamma_{gender(g)}+v_g$
两种任务置换测量方式的回归结果:
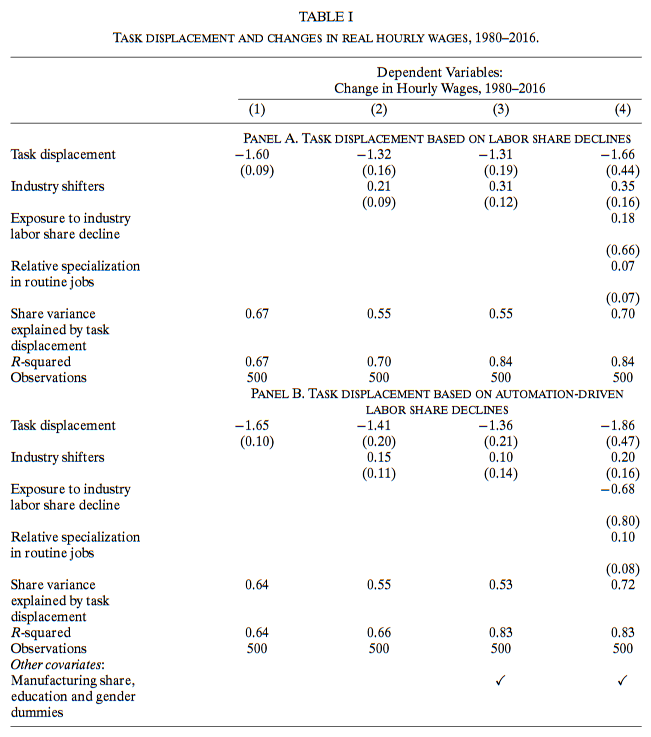
工具变量估计
将第二种测量作为工具变量估计,使用2SLS估计得到类似结果。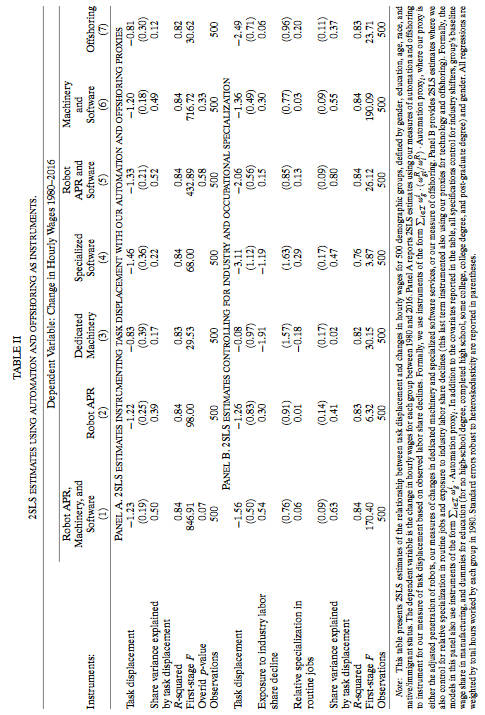
Panel A 第一列是对上一个表格第三列的扩展,与第二种测量方法结果近似,任务置换工资变化变异的50%。第1~6列无法拒接全部一致的假设,符合这些技术通过任务置换的方式施加影响的假设限制。
Panel A的第7列使用外包数据作为工具变量, 它同样为任务置换和受影响群体的真实工资下降贡献了解释,但仅解释了工资变化的12%变异。
Panel B是上一表格第4列的扩展,与Panel A结果近似,虽然不如Panel A精确。
任务置换与SBTC
作者对任务置换和不同形式的SBTC进行了对比。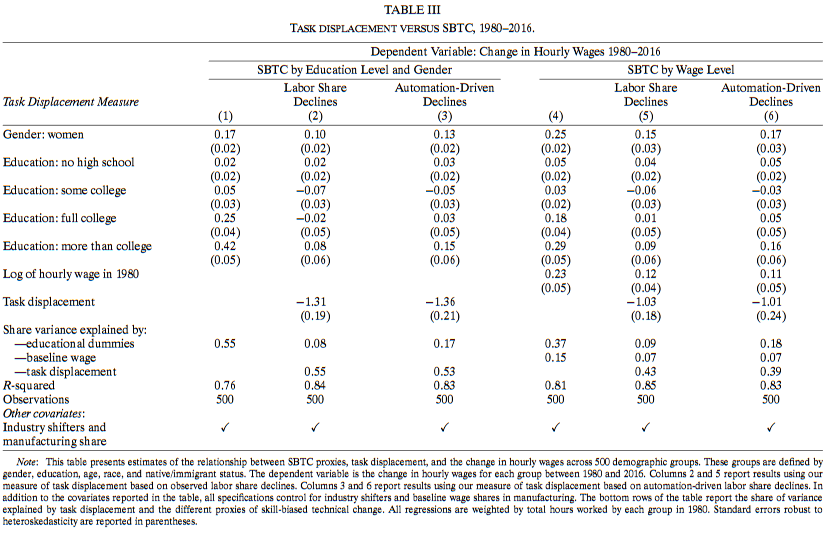
列1显示SBTC变量是显著的,且作用符号符合预期,教育解释了55%的工资变化的变异。然而,当加入了工作置换的变量后(列2 & 列3),教育水平的差异不再显著。工作置换分别解释了80% [(0.42-0.08)/0.42] 和65%的研究生工资溢价,并解释了部分性别工资溢价。整体上,工作置换解释了超过50%的整体工资变化,于此同时教育解释的比例下降至17%。
就业结果
如果工作置换确实导致了对一个人口统计特征群组更低的劳动力需求,那么我们应该不仅观察到工资下降,同时也能观察到就业减少。
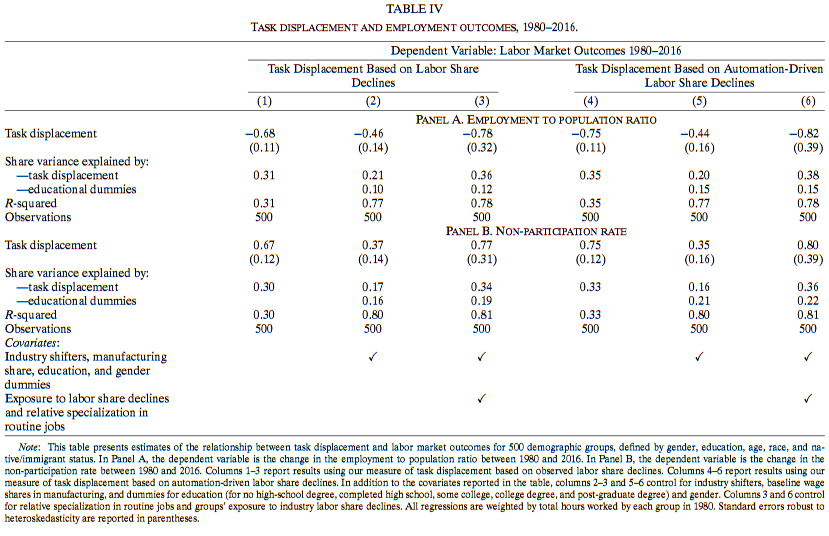
结果与预期一致,Panel B表明工作置换带来的大部分变化是通过不参与就业导致的。但就业效应不反应全部劳动力份额下降行业/常规工作工人面临的不良趋势。
资本、全要素生产率、去工会化、进口和利润
为避免其他工业级的趋势与自动化技术导致的劳动力份额效应相混合,作者对这些趋势进行了处理。结果显示,当控制了自动化测量量,这些趋势与劳动力下降没有显著的相关性。
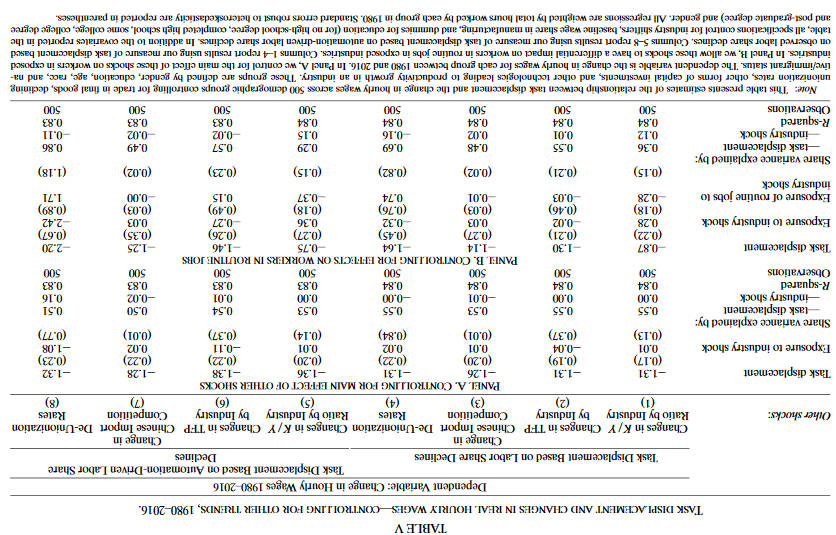
另一个重要的担忧是产业集中度和利润会影响劳动力份额和工资结构。结果同样表明不影响结论。

地域差异
作者将美国地区分为多组进行检验。Panel A包含9个美国区域的300个人口统计特征组;Panel B通过吸收影响人口组别的所有全国性趋势的固定效应,分离了区域和全国变化。结果表明,工作置换变量负向显著,但影响稍小,因此工作置换在地区级别很重要,虽然在理解工资结构的演化方面不如全国性趋势那么重要。
Panel C、D包含722个美国社区区域,通过54个粗略的性别、教育、年龄和种族分组重复了Panel A、B,结果与之相似。

作者还在附录中进行了其他稳健性检验,所有的检验都支持结论。
一般均衡效应与量化分析
简化形式的分析忽视了3个一般均衡效应。
- 常见的生产力对真实工资的影响在截距项中,使估计不能反应工资水平的变化
- 模型没有分离由自动化引起的产业转移,丢失了自动化冲击的一个环节
- 回归分析仅考虑了通过工作置换带来的自动化直接影响,没有考虑涟漪效应。
一般均衡效应与传播矩阵
总体任务份额$\Gamma_g(w,\zeta,\Psi)=\sum\limits_{i\in\mathcal{I}}\mathop{\underbrace{s_i^Y(p,c)\cdot(A_i,p_i)^{\lambda-1}}}\limits_{=\zeta_i}\cdot\mathop{\underbrace{\frac{1}{M_i}\int_{\tau_{gi}}\psi_g(x)^{\lambda-1} dx}}\limits_{=\Gamma_{gi}}$
是对特定行业任务份额$\Gamma_{gi}$的加权求和。其中产业转移$\zeta=(\zeta_1,…,\zeta_I)$。
为刻画涟漪效应,考虑任意技术变化对群组$g$的真实工资有直接效应$z_g$。例如自动化技术的的$z_g$为$g$群组的任务置换效应。使用$z$表示$z_g$的列向量,并对$w_g=(\frac{y}{\mathscr{l}_g})^{\frac{1}{\lambda}}\cdot A_g^{\frac{\lambda-1}{\lambda}}\cdot\Gamma_g^{\frac{1}{\lambda}}$求微分
$d\ ln\ w=z+\frac{1}{\lambda}\frac{\partial ln\Gamma(w,\zeta,\Psi)}{\partial ln\ w}\cdot d\ ln\ w\Rightarrow d\ ln\ w=\mathop{\underbrace{(1-\frac{1}{\lambda}\frac{\partial ln \Gamma(w,\zeta,\Psi)}{\partial ln\ w})^{-1}\cdot z}}\limits_{\Theta}$
其中,$\frac{\partial ln \Gamma(w,\zeta,\Psi)}{\partial ln\ w}$为$ln\Gamma(w,\zeta,\Psi)=(ln\Gamma_1(w,\zeta,\Psi),…,ln\Gamma_G(w,\zeta,\Psi))$对工资$w$向量的$G\times G$雅各比矩阵,并将之作为传播矩阵。虽然传播矩阵比特定任务的生产力函数$\psi_g$的全集要低维,但是它完全解释了涟漪效应和技术变革的一般均衡影响。
传播矩阵具有几项性质。$\theta_{gg’}>0$捕获了群组$g$和$g’$之间的任务竞争程度;$\Theta$矩阵的行和$\varepsilon_g$总是介于0和1之间;$\Theta$矩阵对任意两个群组$g$和$g’$总是满足对称性$\varepsilon_g-\theta_{gg’}/s_{g’}^L=\varepsilon_g’-\theta_{g’g}/s_g^L$ (其中$S_g^L$为群组$g$的劳动份额总和);$\Theta$矩阵的元素指定不同的工人是q互补还是q替代的,当且仅当$\Theta_{gg’}>s_{g’}^L\cdot\varepsilon_g$时$g’$型工人供给增加,$g$型工人真实工资下降。
(下文将传播矩阵的第g行写成$\Theta_g=(\theta_{g1},…,\theta_{gG})$)
LLM认为‘q-complements'用于区分不同类型的互补,'q'指代工人拥有特定的技能或任务。q互补指两类工人拥有在生产过程中相互补充的技能-
命题4—GE效应:自动化对工资,产业价格和总量的影响
$d\ ln\ w_g=\Theta_g\cdot (\frac{1}{\lambda}d\ ln\ y+\frac{1}{\lambda}d\ ln\ \zeta-\frac{1}{\lambda}d\ ln\Gamma^{auto})\ for\ all\ g\in G$
$d\ ln\zeta_g=\sum\limits_{i\in\mathcal{I}}w_{gi}\cdot(\frac{\partial ln\ s_i^Y(p)}{\partial ln\ p}\cdot d\ ln\ p +(\lambda-1)\cdot d\ ln\ p_i)\ for\ all\ g\in\mathcal{G}$
$d\ ln\ p_i = \sum\limits_{g\in\mathcal{G}}s_{gi}^L\cdot(d\ ln\ w_g-d\ ln\ \Gamma_{gi}^{auto}\cdot\pi_{gi})\ for\ all\ i\in\mathcal{I}$
$d\ ln\ tfp=\sum\limits_{i\in\mathcal{I}}s_i^Y(P)\sum\limits_{g\in\mathcal{G}}s_{gi}^L\cdot d\ ln\ \Gamma_{gi}^{auto}\cdot\pi_{gi}$
$d\ ln\ y=\frac{1}{1-s^K}\cdot(d\ ln\ tfp+s^K\cdot d\ ln\ s^K)$
$d\ ln\ s^K=-\frac{1}{s^K}\sum\limits_{g\in\mathcal{G}}s_g^L\cdot(d\ ln\ w_g-d\ ln\ y)$
其中,$d\ ln\Gamma^{auto}=(\sum\limits_{i\in\mathcal{I}}w_1^i\cdot d\ ln\Gamma_{1i}^{auto},…,\sum\limits_{i\in\mathcal{I}}w_G^i\cdot d\ ln\Gamma_{Gi}^{auto})$
$d\ ln\zeta=(d\ ln\zeta_1,…,d\ ln\zeta_\mathcal{G})$
$d\ ln\ p=(d\ ln\ p_1,…,d\ ln\ p_I)$
真实工资变化依赖于生产力效应$d\ ln\ y$,产业结构的诱发转变$d\ ln\zeta$和所有群组经历的直接任务转置$d\ ln\Gamma^{auto}$。由于涟漪效应的存在,直接影响左乘了传播矩阵$\Theta$的第$g$行,在直觉上是群组的工资变化依赖于与他们竞争相同任务的其他群组是否从他们的任务中被淘汰。
与之前一样,我们可以通过该命题计算自动化对工资、产业份额、价格、TFP、GDP和资本份额全部的般均衡影响。此外,需要指定跨产业的完整需求系统来决定技术变化如何影响产业组成,并进一步影响工资结构;也需要参数化并估计传播矩阵来说明自动化内生的任务重配及导致的涟漪效应。
该命题表明自动化产生的直接任务置换是导致任务份额变动的外生冲击,而传播矩阵中编码的涟漪效应与产业构成变化决定了任务置换的全部一般均衡影响。
参数化、校准与估计
本章采用依赖假设2的更普遍化任务转置测量,同时放松了固定替代弹性$\lambda=1$的假设。
在产业$i$中群组$g$经历的自动化驱使任务置换$d\ ln\Gamma_{gi}^{auto}=\frac{w_{gi}^R}{w_i^R}\cdot\frac{-d\ ln\ s_i^{L,auto}}{1+(\lambda-1)\cdot s_i^L\cdot\pi_i}$
其直接任务替代效应为$Task\ displacement_g^{direct}=\sum\limits_{i\in\mathcal{I}}w_g^i\cdot\frac{w_{gi}^R}{w_i^R}\cdot\frac{-d\ ln\ s_i^{L,auto}}{1+(\lambda-1)\cdot s_i^L\cdot\pi_i}$
分母上的$1+(\lambda-1)\cdot s_i^L\cdot\pi_i$是调整成本减少$\pi_i$后的自动化任务替代。
令产业$i$的资本与劳动力替代弹性$\sigma_i=1,\lambda=0.5,\pi_{gi}=\pi_i=30%$。
产业需求:使用简单CES需求$s_i^Y(p)=\alpha_i\cdot p_i^{1-\eta}$,根据文献其中产业间替代弹性$\eta=0.2$
传播矩阵:根据对称性,参数化两个人口统计群组的竞争程度与他们n($n\in \mathcal{N}$)维度距离有关$\theta_{gg’}=\frac{1}{2}(\varepsilon_g-\varepsilon_{g’})\cdot s_{g’}^L+\sum\limits_{n\in\mathcal{N}}\beta_n\cdot f(d_{gg’}^n)\cdot s_{g’}^L\ for\ all\ g’\neq g\ and\ \theta_{gg}=\theta\ for\ all\ g$
其中$f$是群组$g$和$g’$之间给定$n$维距离$d_{gg’}^n$的递减函数,$\beta_n\geq 0$表示在中介涟漪效应上的$n$维重要性。距离由职业和产业就业份额(考虑所执行任务的重叠)和按年龄划分的教育程度(该方法允许未上过大学的人也被测量)。
基于这些参数,假设4中的工资变化可以被写成
$\begin{aligned}d\ ln\ w_g &= \frac{\varepsilon_g}{\lambda}\cdot d\ ln\ y-\frac{\theta}{\lambda}\cdot Task\ displacement_g^{direct}-\sum\limits_{g’\neq g}(\frac{1}{2}(\frac{\varepsilon_g}{\lambda}-\frac{\varepsilon_{g’}}{\lambda})+\sum\limits_{n\in\mathcal{N}}\frac{\beta_n}{\lambda}\cdot f(d_{g,g’}^n))\cdot s_{g’}^L, and\ \beta_n\geq0\\ &s.t.\ \theta+\sum\limits_{g’\neq g}(\frac{1}{2}(\varepsilon_g-\varepsilon_{g’})+\sum\limits_{n\in\mathcal{N}}\beta_n\cdot f(d_{g,g’}^n))\cdot s_{g’}^L,and\ \beta_n\leq0\end{aligned}$
约束条件代表涟漪效应,$f$被设定为倒置的sigmoid函数,误差项$u_g$源自$g$组未被注意的工资影响。在向量上,$\mathbf{u}=\Theta\cdot\mathbf{v}$。为了参数估计,作者施加了一个排除限制,每组任务转置$Task\ displacemetn_g^{direct}$与$\mathbf{u}$正交,或与$\mathbf{v}$等价。
$\mathbb{E}[v_g\cdot(1,Task\ dispalcement_g^{direct},{\sum\limits_{g’\neq g}f(d_{g,g’}^n)\cdot s_{g’}^L\cdot Task\ displacement_{g’}^{direct}}_{n\in\mathcal{M}})]=0$, $g= 1,…,G$
一般均衡估计
最后一列通过作者倾向的方式测量任务置换。第一个面板总结了自动化对工资结构的影响。图表的Panel A展示了普通生产力效应$\frac{1}{\lambda}\cdot d\ ln\ y$为所有群组提升了近45%的工资。Panel B加入了自动化引起的产业组成变化$\frac{1}{\lambda}\cdot d\ ln\zeta$,由于$\eta<1$,自动化会引起的向自动化程度低的部门(如服务业)的转移,并增加这些行业的人员需求,然而这一效应对美国薪资结构的影响是轻微的。Panel C加入了直接任务置换效应$-\frac{1}{\lambda}\cdot d\ ln\Gamma^{auto}$,它产生了相当大的工资变化离差,导致一些组别实际工资下降了25%,并解释了美国1980~2016年薪资结构的总体变化的94%。Panel B和Panel C的对比表明,自动化对工资结构最大的冲击就是通过直接任务置换产生的。与简化形式分析对比,可知涟漪效应使被置换的群组能增竞争有其他群组完成的非自动化任务,从而将置换效应扩散到各个群组之中。
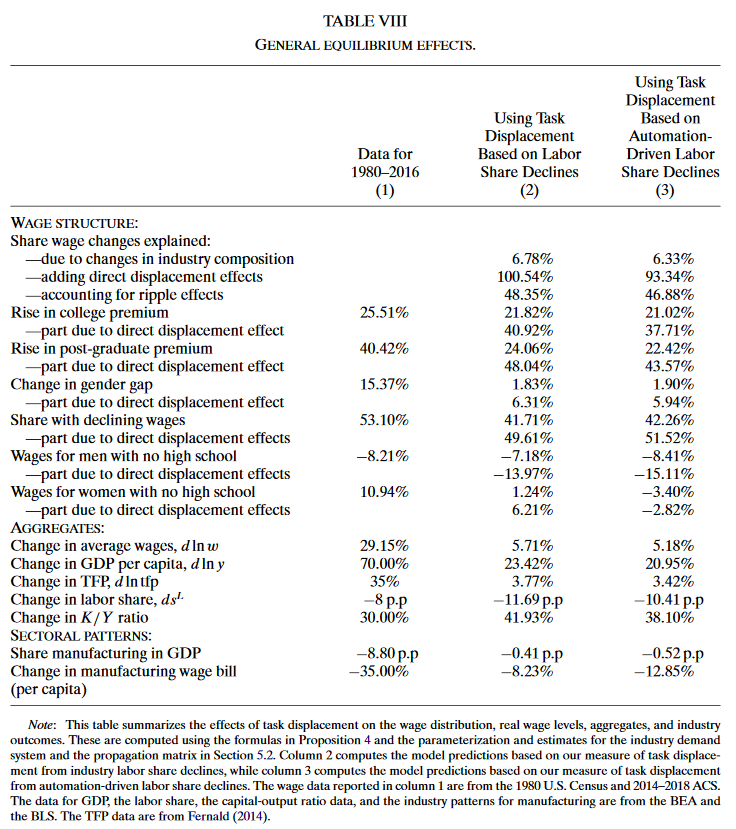
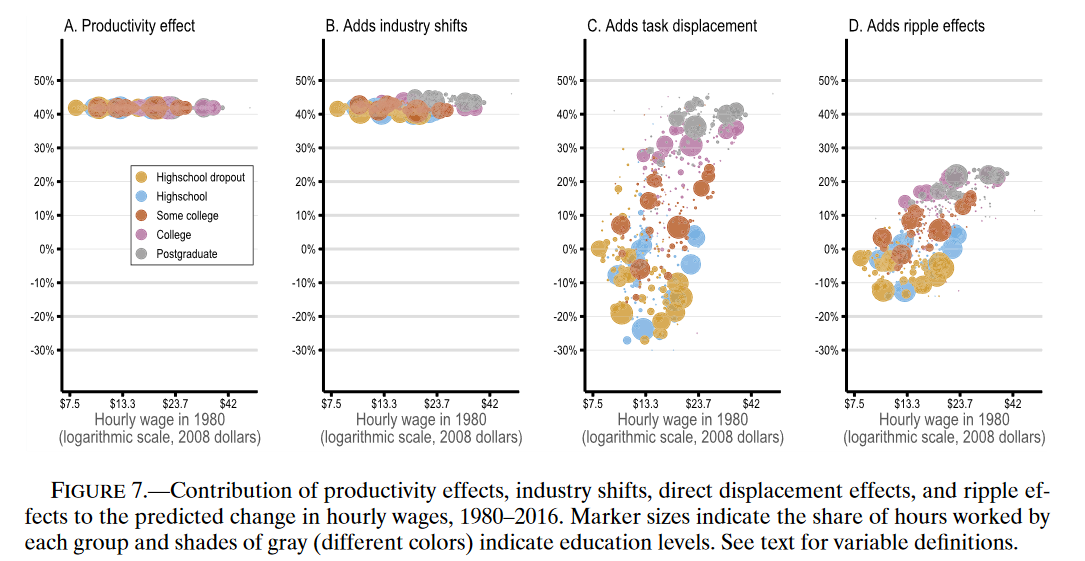
下图绘制了工资变化的预测模型和真实工资变化。
这一期间的劳动力市场中,虽然生产力效应很大(约45%),但仍然由于自动化效应而有所下降。工作置换效应创造了21%的大学溢价和22%的研究生溢价。此外,任务置换仅能将性别差距缩小2%,涟漪效应会抑制自动化直接效应对性别差异减少的作用。
模型没有解释受过高教育的工人工资增长的很大部分,作者可能是新技术之间的互补性或高技能职业赢者通吃等原因。
任务置换在1980~2016年间仅累计获得3.4%的TFP提升,因此平均真实工资增长缓慢,还有很多组别真实工资下降。任务置换对产业结构的整体影响也是微小的,但对制造业比较大。
任务置换解释了结构上劳动力份额下降及资本-GDP比值增加。
做“好”研究必读文献清单
珞珈管理发布了一个经典文献清单,主要包括Foundations of Behavioral Research、Theory and Theoretical Contributions、Scale Development and Common Method Variance、Mediation, Moderation, and Congruence Analysis、Multilevel Modeling and Its Applications、Moderated Mediation and Mediated Moderation in Mono-level and Multilevel Frameworks、Longitudinal Design and Data Analysis、Missing Data, Causality and Endogeneity几个常见主题,先存再说。
业界动态
用户行为分析模型实践——H5通用分析模型
这篇文章主要针对H5埋点,目前H5网页埋点的自由度比较高,导致业务中埋点的重复劳动较多,因此作者提出了一个系统性的埋点分析框架提高分析效率。
作者认为应用上线的初期主要关注用户访问情况和留存情况相关指标,并给基于此构建了分析框架。
- 基础分析
- 用户浏览次数、人均访问页面数、人均使用时长、新老用户访问数据
- 页面分析
- pv、uv、访问时长
- 留存分析
- 留存率
这些指标基本上就是目前业界通用的度量,没有太多新意,也不涉及具体分析目的。
比如我的个人学术Blog使用百度统计做的埋点分析。(其实只是加了个百度统计API,都是它自己干的)
数据惨淡,基本都是我自己、挂的代理,以及应该有几个采集爬虫。居然真的有用户看orz,有从我github进的,居然有必应进的orz,好紧张…..


埋点方案
- 自动采集
前端开发者通过引入h5sdk.js打开自动采集开关(如网页注入百度统计hm.js),脚本按照给定规则进行页面监听EventListener,当用户活动触发对应的事件时会组装数据,之后通过HTTPS传入后台。
实践中,直接统计网页停留时长是不准确的,例如用户缩小浏览器、tab到其他网站等失去焦点行为需要额外处理。
- 三大规则场景
- URL变化时触发事件,进行采集
- URL变化=window.location.origin+window.location.pathname+window.location.hash三部分中任意一个变化,不包含window.location.search变化
- 目前多数网站多是SPA应用,其前端路由有hash模式和history模式两种,当通过前端路由页面切换时,肯定会触发hash模式或history模式相关API
- 对两种模型进行EventListener
- window.hashchange事件——hash模式
- window.popstate事件、pushstate & replacestate自定义事件——history模式
- 对两种模型进行EventListener
- 页面得到焦点focus、失去焦点blur
- tab切页visibilitychange事件
- URL变化时触发事件,进行采集
若一个行为同时满足2个或以上的规则时,只好选取一个规则上报数据
埋点设计
埋点通常成对出现,页面进入-离开、得到焦点-失去焦点、tab-返回。
2个埋点能够覆盖上述3种规则场景,方便计算页面停留时长且便于逻辑判断避免重复。
- 参数设计
- 开发者传入参数
- unique_id:用户唯一标识
- topic_id:网站唯一标识
- current_env:网站环境,默认prod
- SDK内部获取参数
- duration:页面停留时长
- last_page_url:上一页面URL
- page_url:当前页面URL
- SDK需要参数
- eventType
- 用户自定义参数
- 开发者传入参数
数据上报
兼容性&容错性
兼容性依赖于window对象
容错性:try catch
个人数据保护合规
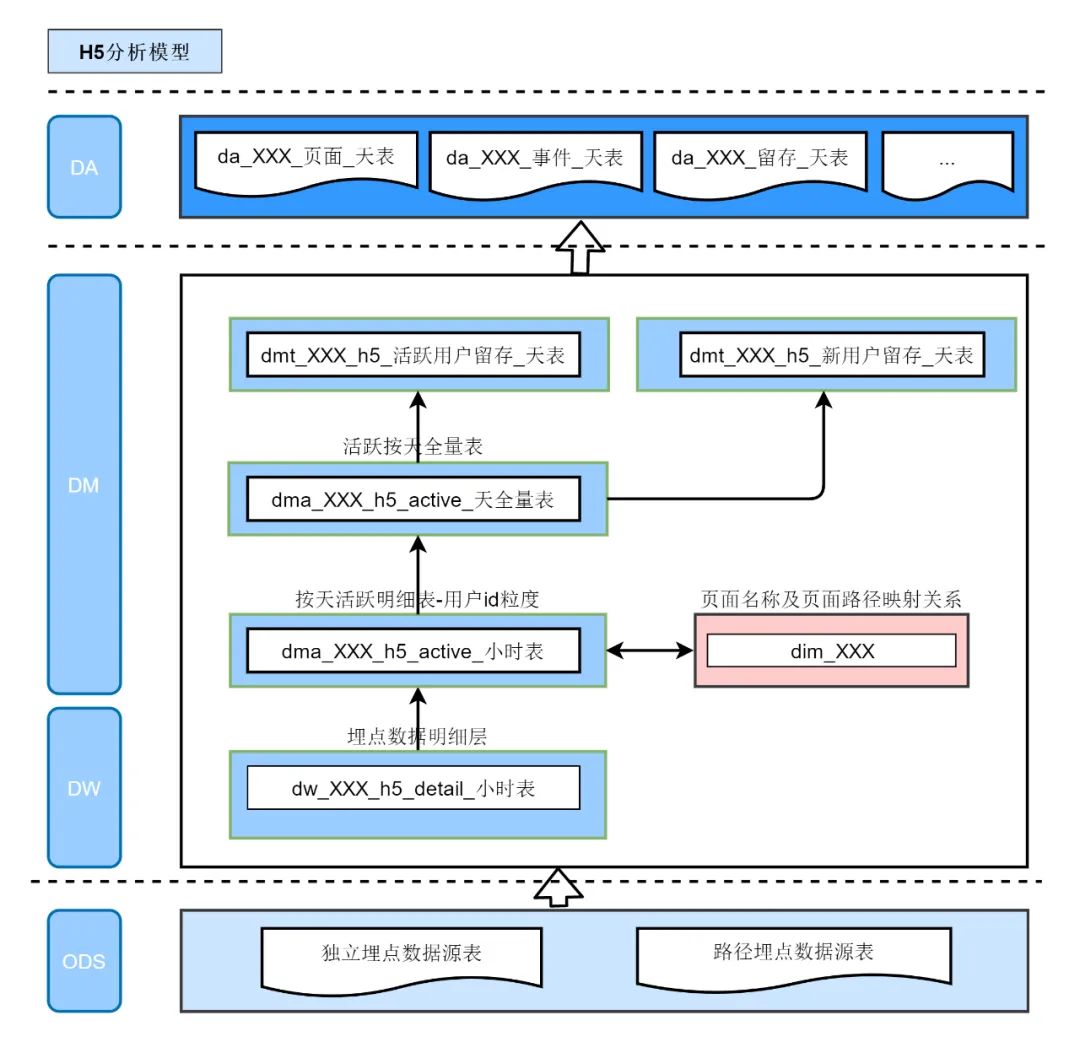
数仓方案
数据展示
消费电子与家居生活2022-2023年度行业报告&新趋势洞察丨36氪研究院
利益关联:抖音商城参与并提供数据,存在主观偏差
调研问题:消费电子&家居行业发展与消费者洞察
调研人员:36氪研究院、抖音电商
调研日期:——
调研范畴:家具家电&3C数码
调研对象:具有购买力和购买欲望的2000名消费者与潜在消费者的人口统计特征、认知、决策、购买及需求行为变化
调研方法:桌面研究、调查问卷
调研结论:
-
消费电子&居家产品稳步增长
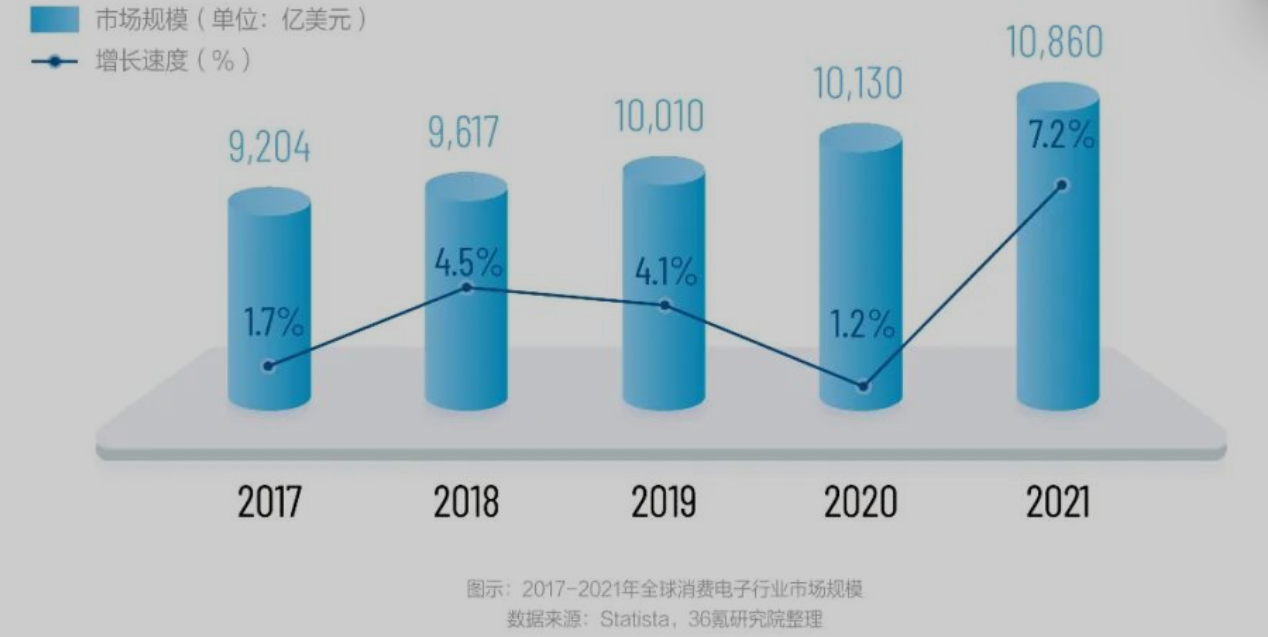
- 电子产品快速迭代
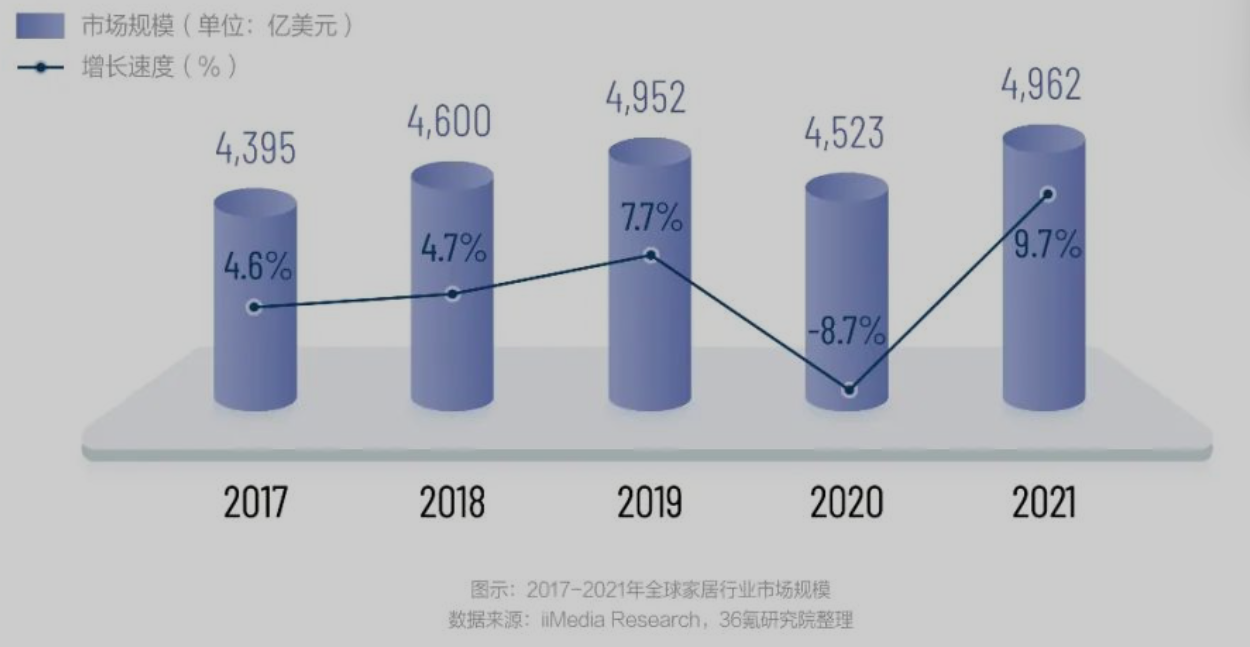
- 家电生活对宏观经济变化敏感型高,回暖向好
- 数字化技术带来经济价值提升
- 线上销售渗透率提升
- 电子产品快速迭代
-
消费电子与智能家居的应用场景多元化
-
作为终端设备交互入口的5G智能手机出货量提升
-
智能家居主要面向视频娱乐、家庭监控、智能照明等场景
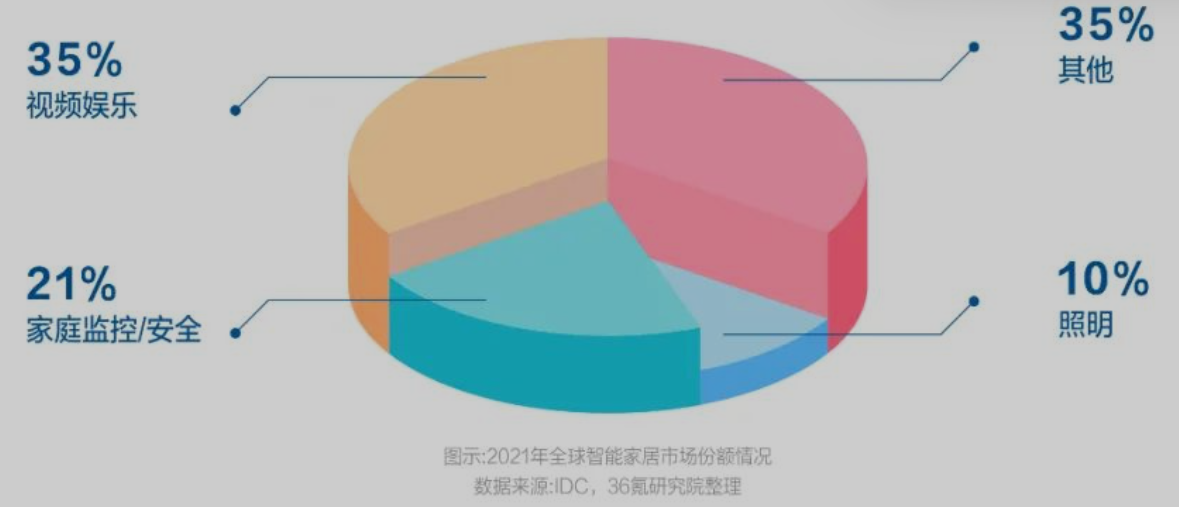
-
集中于娱乐和控制两个方面,与我期待的智能家居不一致
主要满足保健需求,激励需求的增益不足
-
-
中国消费电子&智能家居内生韧劲强
- 中国拥有全产业链,消费电子产量占全球70%+
- 家居产业增势强,韧性足
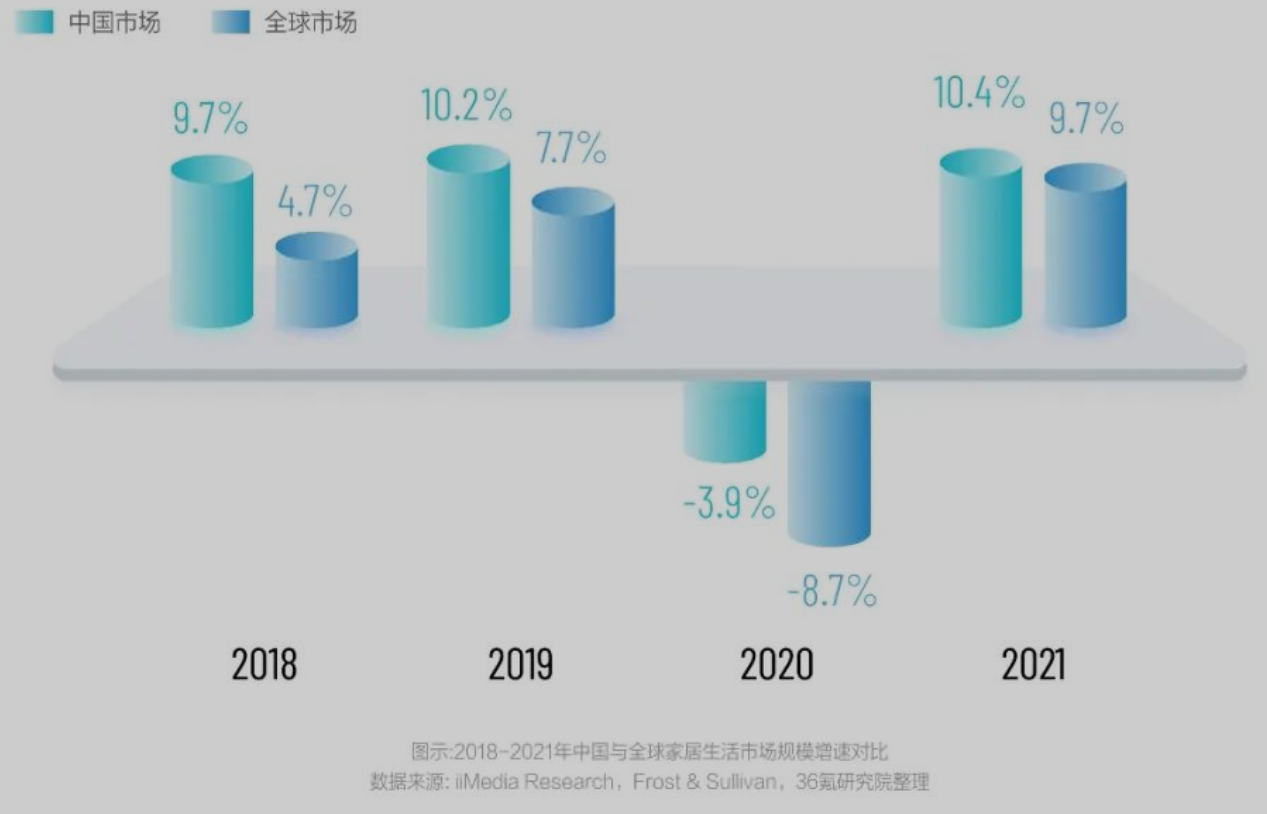
- 消费电子电商渗透率40%~50%
- 家居产品(非智能家居)渗透率不足10%
- 抖音投稿持续增长(图表没有纵坐标,不可信)
-
-
消费者洞察
- 59.8%被试期待智能产品解决生活琐事、轻松享受生活
- 什么是琐事?
- 54.3%期待低碳环保、低耗节能
- 50.9%期待安全健康
- 50.7%期待居家生活自在,丰富多彩,快乐
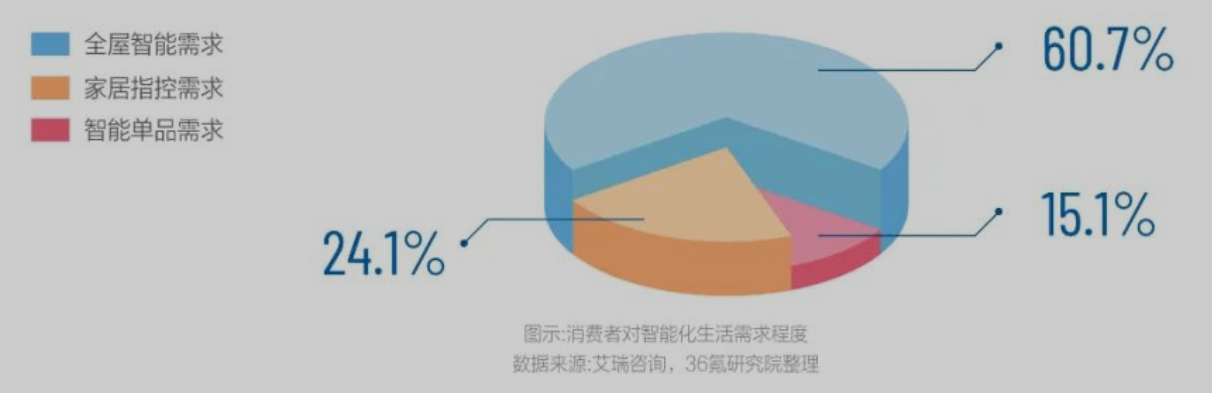
- 59.8%被试期待智能产品解决生活琐事、轻松享受生活
技术技巧
Python库: 制作各种用途的二维码
1
2
3
4
5
import segno
qrcode = segno.make("文字内容/URL")
qrcode.save('qrcode.png', scale=4) # .save/.show
该python库还可以定时发送邮件、发起电子支付、打开地图等。
Python 实现各种算法及其可视化展示丨github 标星15.5w
-
Fan, J., Sun, T., Liu, J., Zhao, T., Zhang, B., Chen, Z., Glorioso, M., & Hack, E. (2023). How well can an AI chatbot infer personality? Examining psychometric properties of machine-inferred personality scores. Journal of Applied Psychology. https://doi.org/10.1037/apl0001082 ↩
-
Belcastro, L., Marozzo, F., Talia, D., Trunfio, P., Branda, F., Palpanas, T., & Imran, M. (2021). Using social media for sub-event detection during disasters. Journal of Big Data, 8(1), 79. https://doi.org/10.1186/s40537-021-00467-1 ↩
-
Acemoglu, D., & Restrepo, P. (2022). Tasks, Automation, and the Rise in U.S. Wage Inequality. Econometrica, 90(5), 1973–2016. https://doi.org/10.3982/ECTA19815 ↩