• 学术相关
  • 网络内容流行性阶段（如爆发）预测方法
  • 【科研数据分享】推荐系统数据集汇总
• 技术技巧
  • 淘宝用户购物行为数据可视化分析
• 娱乐
  • 文献丨社会韧性及其建模
    • 韧性概念
    • 社会系统韧性
    • 社会组织韧性建模
    • 韧性计算
    • 网络构建和干预

学术相关

网络内容流行性阶段（如爆发）预测方法¹

作者一上来就做出假设：社交媒体线上内容流行度的演变包含多个阶段。作者认为前人的研究过多集中在预测流行性的总量和级别上，缺少对流行性过程和趋势的分析，因此作者致力于对社交媒体内容的动态演化进行建模。

作者采用的社交媒体平台为新浪微博，流行度的测量采用转发数，并解释其认为转发是社交媒体网络信息扩散的核心驱动。很明显作者缺乏足够社会科学认知，采用了一个简易的测量方式，这是计算机领域学者研究中常见的问题，进而导致这些研究在业界实际运营中会产生一定的问题。因此，跨学科合作仍然是最佳选择。现有研究中是否有合适的网络信息测量呢？目前常用的措施都是将转发、浏览、点赞作为指标，它们对特定的问题背景，如商业、时事信息传播，应该如何加权综合或引入其他指标？

现有的研究主要采用三类方法建模流行性：区分方法、生成方法、基于深度学习方法。区分方法主要依赖特征工程，并构建有监督的分类模型。区分方法比较灵活，但经常使用静态特征，不擅长处理动态流行性演化。生成方法通常建模描述用户行为或流行性时间序列的生成过程。生成方法具有较好的可解释性，但通常需要强假设且计算复杂度比较高。深度学习方法通常效果更好，但是需要大量的训练数据且不可解释。

问题建模

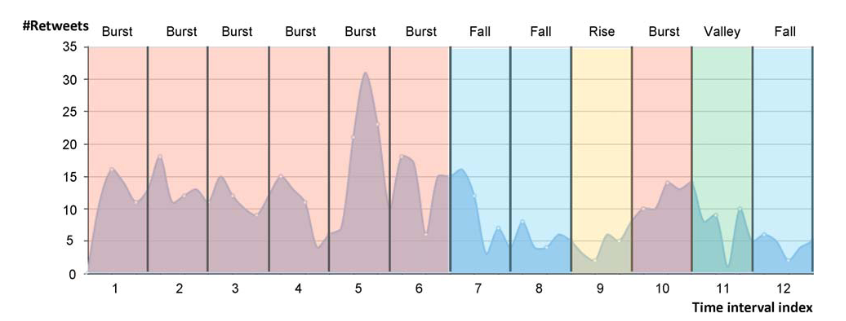
上升阶段—爆发阶段—下降阶段—低谷阶段

线上内容的生命周期被分割为$K$个等长的时间窗。第$k$个时间窗内，不同时间单元（更短周期）新转发数为$s_{k1},s_{k2},…,s_{kn}$，$n$为每个时间窗内时间单元数。

当第$k$个时间窗口满足$\frac{max{s_{ki}|i=1,…,n}}{\frac{1}{nK}\sum\limits_{k=1}^K\sum\limits_{i=1}^ns_{ki}}>\tau_B$时标记为爆发，当期满足$\frac{min{s_{ki}|i=1,…,n}}{\frac{1}{nK}\sum\limits_{k=1}^K\sum\limits_{i=1}^ns_{ki}}<\tau_V$时定义为低谷。

若不属于爆发/低谷阶段，则对每个时间窗口内拟合OLS，斜率$w_k=\frac{\sum\limits_{i=1}^ns_{ki}(x_i-\bar{x})}{\sum\limits_{i=1}^n x_i^2-\frac{1}{n}(\sum\limits_{i=1}^nx_i)^2}$，可被简化为$w_k = \frac{6\sum\limits_{i=1}^n s_{ki}(2i-n-1)}{n(n^2-1)}$。当斜率$w_k>0$是定义为上升阶段，$w_k<0$时定义为下降阶段。

给定$N$个时间窗口作为输入间隔，接下来的$d$个时间窗口作为响应间隔。

算法模型

Popularity Stage Prediction（PSP）算法为多类别分类算法。

• 先验因子加权算法 Factor Prior Weighting Algorithm — FPW

  • 动态因子

    • 时间窗口内转发数/转发用户

    • 转发树结构—原始推文为根节点

      • 意味着更激烈的讨论
      • 最大深度
      • 平均路径长度（Wiener index维纳指数）

    • 用户回复网络结构

      不同于转发数，记录的是转发用户的树结构

      • 意味更高的互动频率
      • 网络密度
      • 平均度

    • 社交网络结构

      关注网络

      • 平均粉丝数
      • 被关注者数

  • 单一动态因子预测

    • 每个因子对应一个时间序列$v_1,v_2,…,v_t$，$t$为时间窗口
    • 每一个时间序列可以提取一阶导数、二阶导数等特征
    • 基于提取特征构建分类模型（KNN、SVM )预测未来流行阶段

  • 算法

    • 认为不同动态因子捕捉流行性演变的不同方面
    • 每个动态因子的权重为先验因子向量$p_1,p_2,…,p_R$，其中$R$为先验因子数

• 流行阶段聚类算法

  • 前人研究表明短时流行性变化遵从有限数量的模式
  • 应用K-means聚类算法
    • 阶段序列间距离：阶段序列对应位置上，阶段不同的数量
    • 簇数$K=4$
      • Burst; valley; rise; fall
    • ？好像有点问题

• 流行阶段预测算法

  

  • 使用平衡因子$\alpha$组合先验因子加权算法和流行阶段聚类算法

实验结果

使用五折交叉检验，报告平均F1分数，处理了数据不平衡问题。爆发和低谷的阈值由信息安全的专家设置，$\tau_B=3,\tau_V=0.1$。推文的生命周期被划分为10个时间窗口，每个时间窗口有5个时间单元。

基准模型：投票方法、静态因子方法、动态因子方法、LSTM、DeepCAS、DeepHawkes。投票方法、静态因子方法、动态因子方法和本文使用分类器使用SVM。

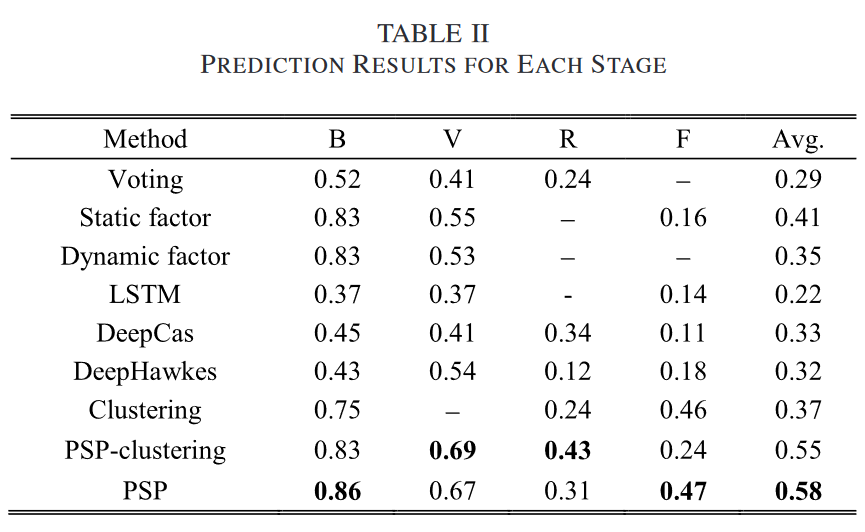
案例

【科研数据分享】推荐系统数据集汇总

​ 涉及电影、书籍、电子商务网站用户行为等竞赛和真实业界数据集

• Retailrocket Recommender System dataset
  • 4.5个月内用户浏览、点击、加入购物车、交易行为
• Outbrain Click Prediction Dataset
  • 用户浏览网站点击行为

技术技巧

淘宝用户购物行为数据可视化分析

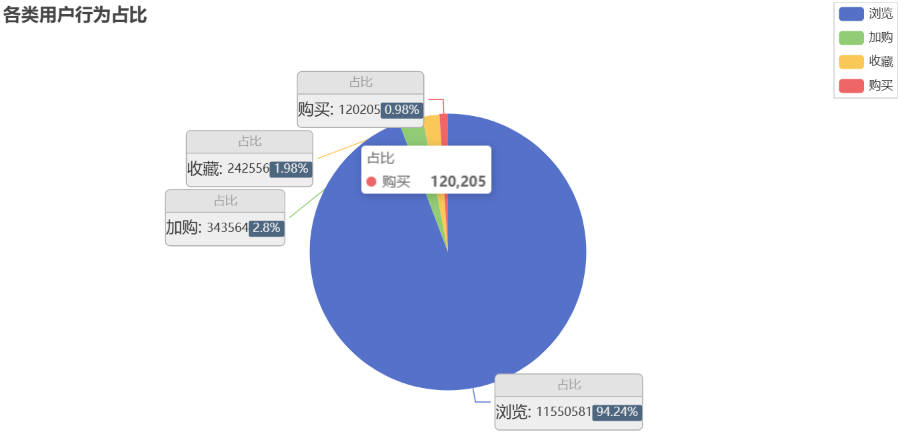
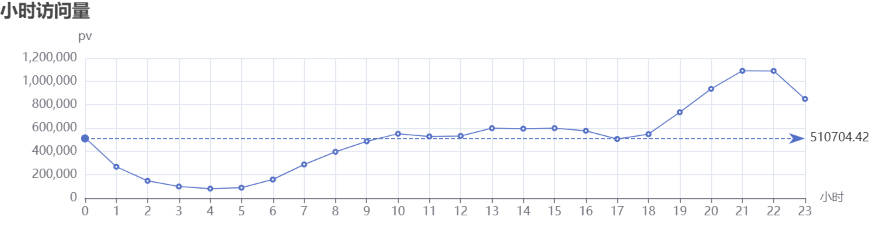
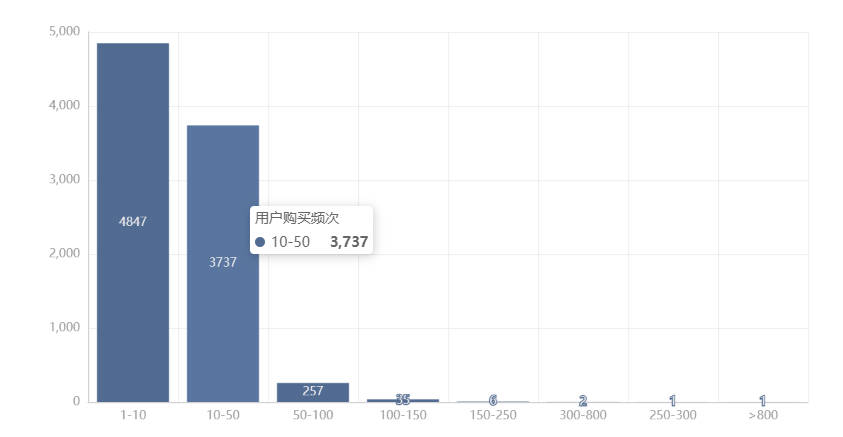
淘宝用户购物行为数据可视化分析

流量分析、ARPU分析、ARPPU分析、复购分析

淘宝用户购物行为数据可视化分析(使用matplotlib)

新增、留存、访问深度、跳失率、漏斗分析、RFM

淘宝用户行为可视化分析——基于pyecharts

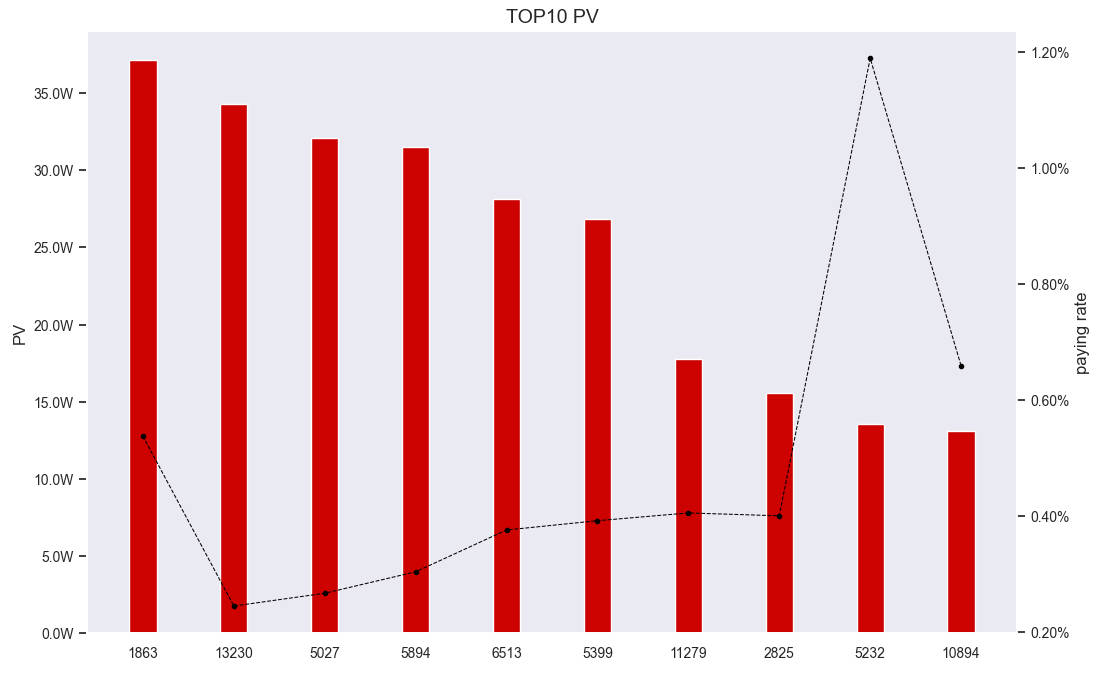
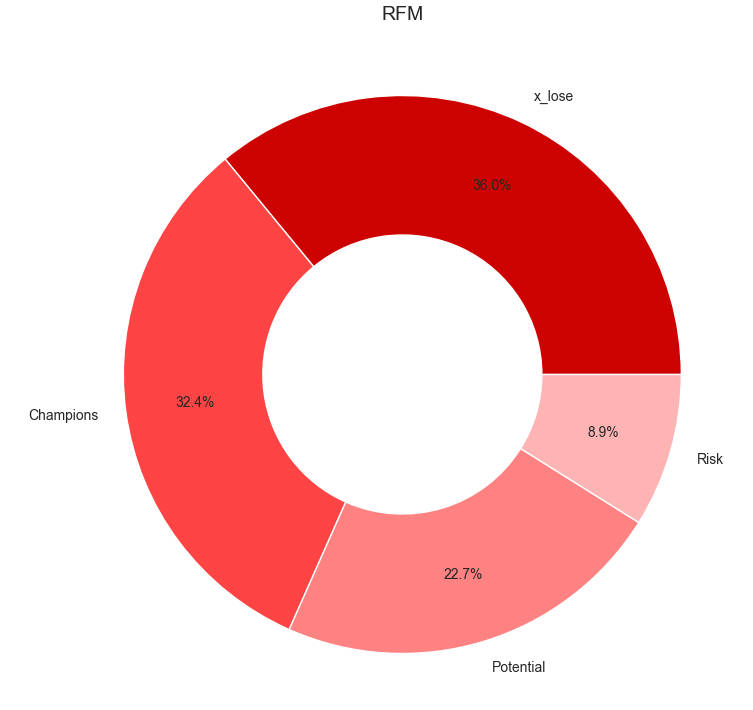
娱乐

文献丨社会韧性及其建模²

这篇文章挺好玩的，但感觉结构组织比较松散，创新点部分很多没讲清楚，方法上有一些不合理的地方，缺少有力的实证。可能作者没有完成，做不下去了。

比较有意思的是通过鲁棒性和适应性衡量社会韧性（不做一个质性吗？），还有用可能的网络结构数量衡量适应性。

应该略读的，但总是期待它下一步有没有什么好玩的做法，大多数有趣点Abstract没讲。

韧性指系统抵御动荡及从冲击中恢复的能力，它是一种系统性的通用动态属性。韧性不仅需要考虑冲击的强度，同时也要求系统拥有吸收不同类型冲击的能力，且必须有能力从冲击中恢复。由于评估对冲击的响应和从不同冲击中恢复的能力，需要考虑到系统的具体情况，因此难以对韧性下达准确定义，作者希望各学科学者基于学科情况自行定义。

作者开发了一个可以即时计算鲁棒性和适应性，进而评估组织韧性的框架，旨在构建一个更宽广的理论基础，并致力于具体解释概念化社会组织问题。

韧性概念

作者首先回顾了对韧性讨论较多的两个领域的知识，工程学和生态学韧性。

• 区分鲁棒性、稳定性和韧性
• 适应性与恢复之间的联系
• 鲁棒性与现有系统风险测量的关系
• 韧性系统是否总是回到稳态

鲁棒性与适应性

虽然不同学科对韧性的具体定义有所差异，但整体上韧性存在部分普遍特征，它与鲁棒性（结构性：抵抗冲击）和适应性（动态性：克服冲击）有紧密关联。

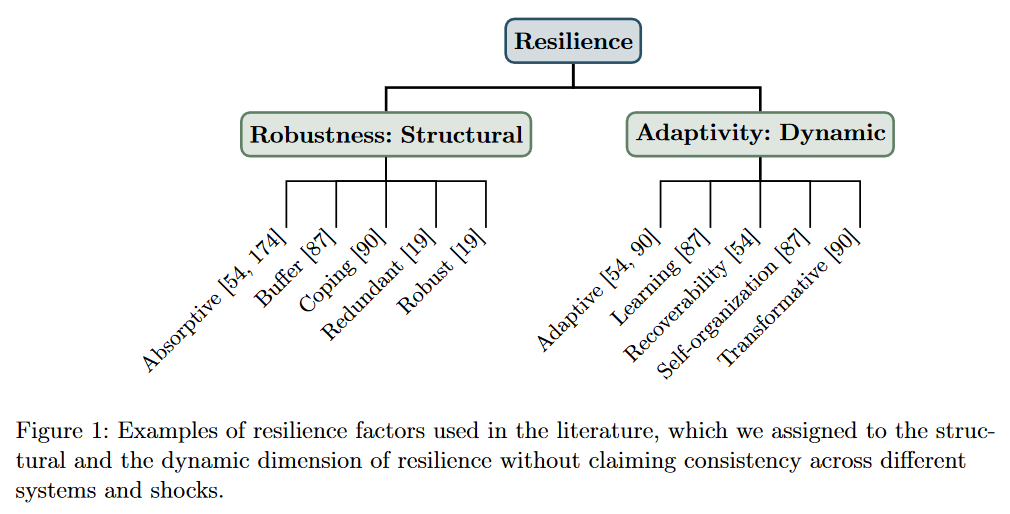
作者从网络拓扑、稳态、反应和创造性破话角度指出了现有韧性测量分析在社会组织方面存在局限性，韧性意味着以可持续方式应对变化。

基础设施系统韧性

在基建领域，韧性也是一个经常被关注的特征，这里的韧性被认为是系统在各种挑战下，维持可接受水平服务的能力。

适应性指现有结构正在运行的过程的潜在动态变化，而非结构变化。但一定程度的鲁棒性可以成为自适应性的先决条件。

韧性与鲁棒性最大的区别在于韧性具有恢复能力，虽然在工程领域这种韧性通常与人类干预有关系，但是将之排除在系统韧性之外，简单地将韧性与鲁棒性等同是不正确的。

量化冲击的影响需要建模系统的反馈，进而才能评估系统性风险。通常鲁棒性被定义为抵抗黑天鹅事件的能力。衡量鲁棒性一般采用损失评估模型，即估计系统元素抵御给定等级的压力或伤害，且没有失能或功能衰退的能力。

然而，单一聚焦于极端事件的鲁棒性评估忽视了系统内部一些轻微伤害引发问题瀑布的放大效应。因此，鲁棒性也需要关注部分系统元素失误的可能性及是否存在该失误被传导放大的机制。许多基础建设网络通过移除部分节点并分析网络影响进行鲁棒性测试。为理解系统的放大机制，我们需不仅要对节点内进行动态建模，也要关注节点间的量化交换，即需要建立耦合动态网络框架。

总的来说，基建领域的韧性过于关注系统的鲁棒性，但分析表明简单的将韧性降维成鲁棒性是存在问题的。

生态系统韧性

历史上，韧性概念第一次被使用就发生在生态学领域。生态系统永远在更新和重组过程，因此，生态学的韧性概念并不将结构上的鲁棒性视作首要特征，转而更关注生态系统在动态上的适应性，如“韧性是一个系统在短暂扰动后重回稳态的能力”。

许多系统事实上是亚稳态的，它们能在小型扰动下保持稳定，但当扰动超过特定级别后就会变得不稳定，系统会脱离稳态，并可能达到新的均衡稳态。【物理学、化学：相变；社会学、生物学：政变】

由于系统会不断地自我演化，所以简单地将生态系统恢复的韧性定义为在扰动后系统是否回归原先状态或达到新的稳态是不正确的，即使没有扰动系统也可能不断变化。更普遍地，韧性被定义为“生态系统在不改变自组织过程和结构的前提下，抵御大量的扰动的能力”，并进一步提出了系统的易损性和敏感性概念。

对于生态系统韧性而言，恢复的时间尺度很重要。如果时间尺度过长，那么系统不会被认为有韧性。所以一个常见的测量是使用生态系统恢复到接近正常状态所需时间的倒数。但问题是韧性本身也依赖时间尺度，例如在当天尺度下，系统可能被认为拥有恢复到正常状态的能力，但是在十年的尺度上，系统可能没有韧性。

因此，将韧性降维成适应性也存在问题。作者认为有韧性的生态系统使用鲁棒性抵御低水平的扰动，之后系统会调整自身使其适应改变后的环境。

进一步的，潜力和连通性也是生态系统韧性的重要概念。潜力决定了系统在未来可选择的转变方向数量，类似于适应性概念。连通性指随着时间推移，产生的高水平内部控制性和有限的应对扰动潜力，类似鲁棒性概念。它指出了高度鲁棒可能产生对韧性的负面影响。

一种观点是生态系统韧性以循环的方式在不断改变，因为不断增强的连通性会，由于不断降低了系统潜力，最终会导致系统崩溃，而在释放阶段系统的连通性较弱，而潜力又较强，因此有很强的重组能力，进而形成循环。作者认为这也符合社会组织的复苏。但是这种循环尚无实证，作者在这方面的推进进行了尝试。

不同时间和空间尺度的适应性循环间的耦合关系，可能导致一个嵌套层次结构——扰沌。

扰沌，是一个科学术语，用来描述不断进化的，与多个元素相互关联的分层系统，为了理解和解决这一难题而提供了一个重要的新的结构框架。在扰沌的系统结构中，包括那些自然（如森林）和人类（如资本主义），以及复杂的人与自然的系统（例如，控制自然资源使用的森林服务机构），在不断的适应性的周期中的“生长、积累、重组、更新”是相互连接的。

什么样的冲击会导致系统丧失韧性是一项关键研究，非参数回归模型或机器学习模型（如符号回归）是常用的分析手段。丧失韧性的早期信号可以在时间序列中被识别，如临街慢化（在扰动中恢复速度变慢）、系统变量自相关增加都有可能是潜在指标。

社会系统韧性

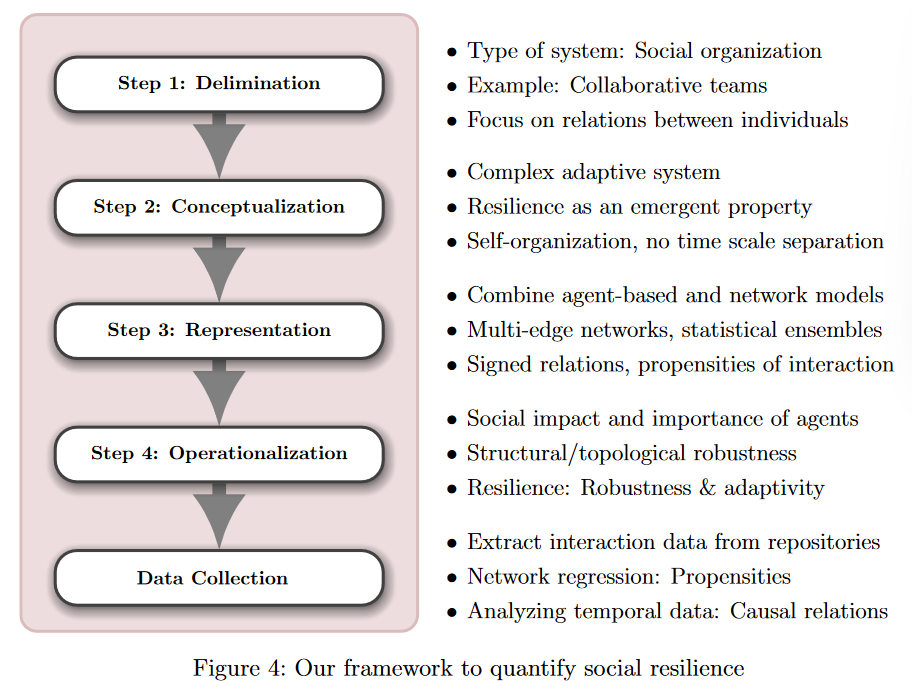
• 范围界定

研究的变量是社会韧性，而非社会中的韧性，需要从系统的角度分析。而研究对象是社会组织或集体，即被嵌入到特定环境并追求集体目标的正式或非正式的相关个体组合。

心理学对个体韧性有较多的研究，但是社会韧性需要将个体整合为集体。作者假设集体拥有$10^2$个个体，这个规模让个体仍然很重要，但又足够大来形成集体。社会韧性不同于个体韧性，也不是个体韧性的简单加和。

作者对社会组织韧性的定义为：“组织或社区应对社会、政治和环境变化带来的外部压力和扰动的能力。”此处定义强调冲击源自组织外部，而非内部流程，这是本篇文章关注的焦点。

社会韧性不止关注在扰动后系统的持久性，同时也关注系统设法增强其未来调整水平的能力。

近期研究表明3个因子对社会系统的韧性有重要影响：对扰动的易损性；对该易损性的预测、预见或态势感知能力；适应能力、灵活性或流动性使其减轻易损性。

量化社会韧性的两大难题包括如何定义一个考虑系统动态变化的韧性测量方法及使用现有数据测量变量。

• 概念化

社会系统是一个复杂适应系统，包含多个大量相互作用的系统元素Agent。作者从微观/Agent视角开始，直至宏观/系统视角理解社会韧性。技术上，作者结合了ABM和时序多层网络模型。

Agents为异质性网络节点，通过社会地位、角色、知识、观点等依赖其他智能体的动态属性刻画。由于极大的社会组织会涌现出内聚力或合作等规模现象，作者的目标并不包括极大的社会组织。在小的系统中，随机影响、路径依赖、局部效应等因素都会对动态产生较大的相对影响，所以让所有智能体以类似方式交互的平均场法是不合适的，我们需要能够反映Agents异质性的模型。

社会组织属于自组织系统，关于协同进化、学习等二阶涌现由于智能体之间的互动而产生，导致系统的动力学特征难以被预测。

社会组织是一个非常不稳定的系统，几乎不能定义一个参考状态，因此无法分离冲击和随后的恢复过程。社会系统的稳健性和适应性变化是在瞬间产生的，且稳态与非稳态难以区分。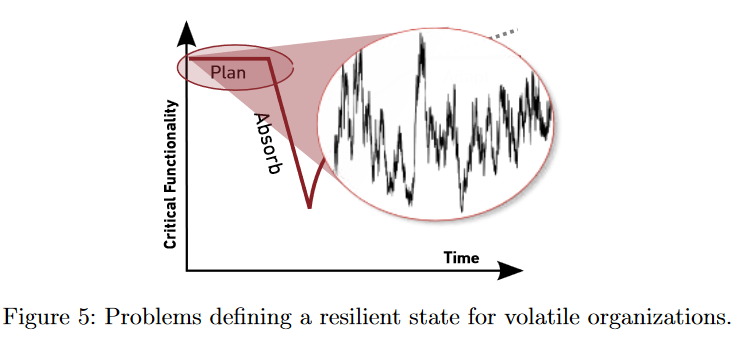

社会组织韧性建模

网络表示

网络是复杂系统建模的一种方式。网络的结点为Agents，边$a_{ij}$表示节点间关系或互动。网络使用邻接矩阵$A$表示，实体间的连接通常是有向的，即$a_{ij}\neq a_{ji}$。一对节点间的连接往往是多重的，即$a_{ij}\geq 1$，且有时间约束$a_{ij}(t)$符合因果顺序。

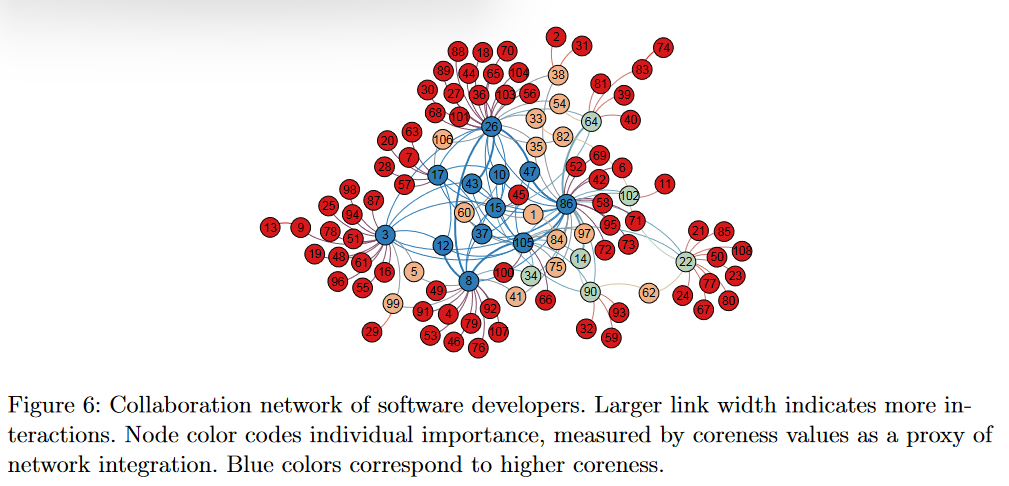
对于社会韧性而言，重要的是Agents之间的社会关联$w_{ij}$，关联拥有正（支持）负（反对）向之分。通常社会交互数据较为常见，但正负向关联数据少有，因此需要从交互数据中推断关系方向。

社会关联符号对社会网络的鲁棒性有关键的影响。考虑3个Agents的三角关系，结构平衡理论认为如果社会结构包含平衡的三元关系，网络就被认为是稳定的。确定平衡状态的经典方法只考虑正负向关联的符号$S_{ijk}=sign(w_{ij})\cdot sign(w_{ik})\cdot sign(w_{kj})$，若$S_{ijk}=1$三角关系是稳定的，若$S_{ijk}=-1$则不稳定，并有向稳定结构转变的趋势。线性指数是衡量不平衡结构向平衡结构转变的最小符号变化数，可被用来测量结构的鲁棒性。

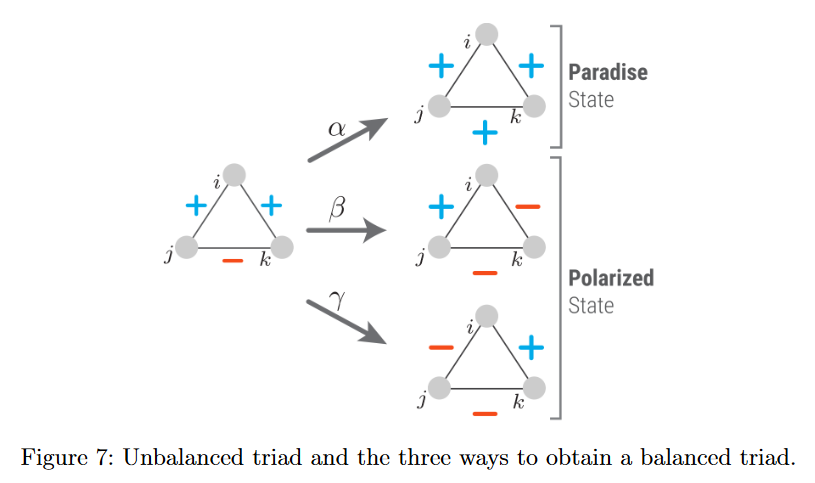
社会组织建模的主要挑战是不仅agents属性存在大量异质性，agents之间的交互也存在大量异质性。例如两个开发者进行协作，处理同一段代码，它可以使用二分图网络表示。协作网络是两个开发者处理同一段代码，则有直接关联的映射网络；代码的映射网络是它们被同一个开发者处理的网络。当两个开发者协同处理多段代码时，每个网络投影的节点会有多个连接，进而形成多边网络。

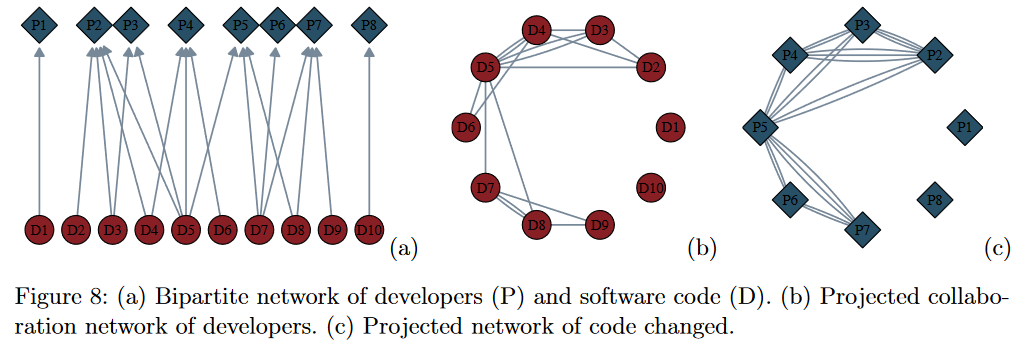
考虑到这些异质性，构建表示社会组织的网络需要从知识图谱（关系图谱）开始，它直观地将个体之间的多种联系方式展示了出来。

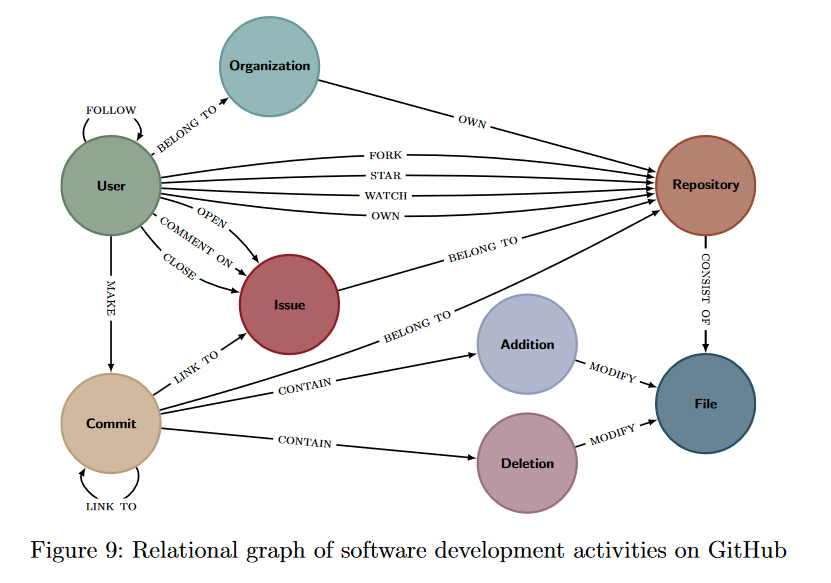
在知识图谱中，我们建立了多种映射，每一个映射都有自己的网络，这些网络组合形成了一个多层网络（multi-layer network）。多层网络中每一层的结点和交互都是不同的。当多层中结点是相同的，但交互关系不同时，称之为多路复用网络（multiplex network）。多层网络可以表示为张量。

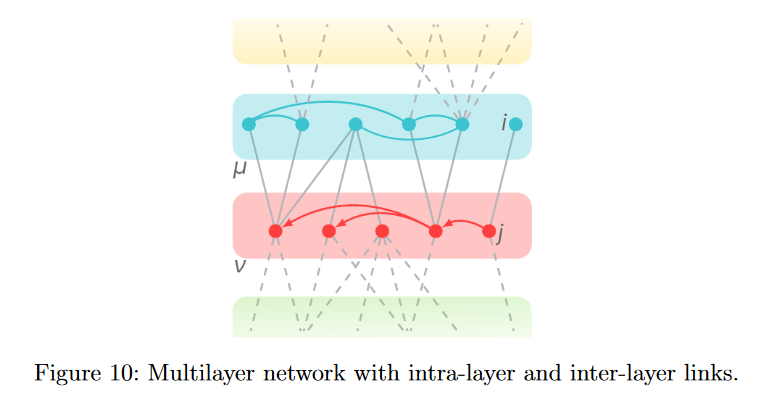
网络在分解为两个Agents之间任意类型交互的双边互动时，存在明显局限性（$C_n^2$连接数过多）。因此，作者使用超图，一种高阶网络，使更高阶节点包含同时互动的Agents群组，群组之间的互动表现为高阶节点之间的连接。第一阶是标准网络，第二阶包含2个Agents的群组，第三阶包含3个Agents的群组，以此类推。超图可以通过跨层连接来表示不同规模群组之间的互动。

网络集成

利用现有数据构建集体网络表示只是一种可能的方法，且不一定是典型方法。理想状态下，我们需要一个所有可能网络出现的概率分布，这样的网络集成很大程度上由Agents之间的连接约束决定。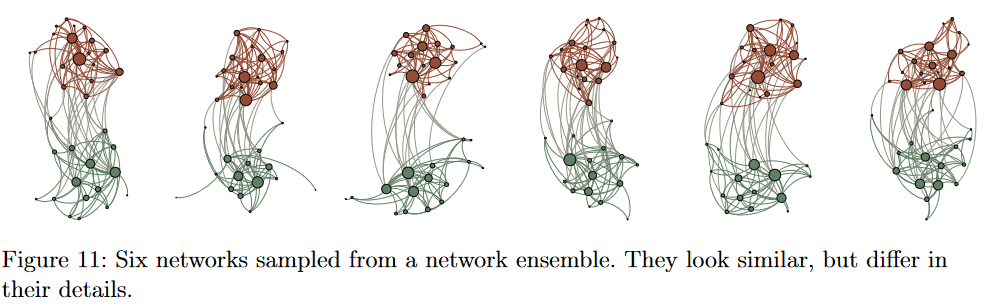

假设不存在连接约束，则对于$n$个节点$m$条边的网络，我们可以组合成大量的随机网络，且每个网络形态都是等概率的。

方法部分作者很多没有交代

作者提出一种广义超几何图谱集成Generalized Hypergeometric Ensemble of Graphs方法来刻画具有异构约束的多边网络模型。该方法使用二元关联倾向$\Omega_{ij}$捕捉节点形成连接的偏好，反映了同质性或互惠等社会机制。gHypEG可以将正式任务整合在班级或社区中，令不同“区块”$k,l$（如社区）的节点$i,j$之间有连接倾向$\Omega_{kl}^B$。被纳入的特征可以通过极大似然估计计算权重。

倾向性$\Omega_{ij}$通过多路复用网络回归计算。每个网络层$l$编码的Agents之间不同类型的已知关系作为解释变量IV。通过拟合$\Omega_{ij}$获得每层对DV交互数量的影响，这样使观察到的网络具有最大可能性。

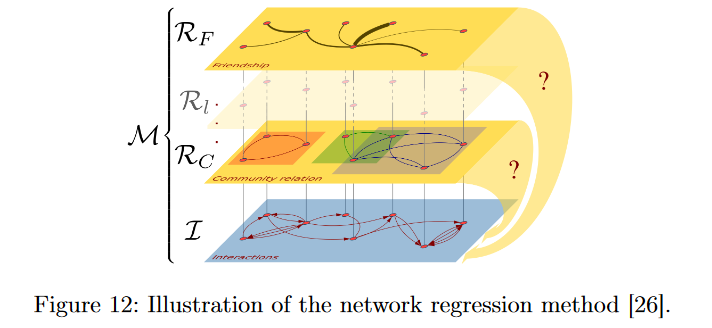
通过标定倾向性，该方法可以计算出在给定链接约束下，观察的网络存在多少种可能结构，进而可以被用于量化网络的适应性能力。作者使用其标准化的香农熵作为潜力值，量化适应能力。

作者使用交互数量来分析社会关系的正负向。当交互数量较多时，社会关系通常是正向的；当交互数量较少，则通常是负向的。两个Agents之间的社会关系权重$w_{ij}=Pr(A_{ij}<\hat{a}_{ij})-Pr(A_{ij}>\hat{a}_{ij})$。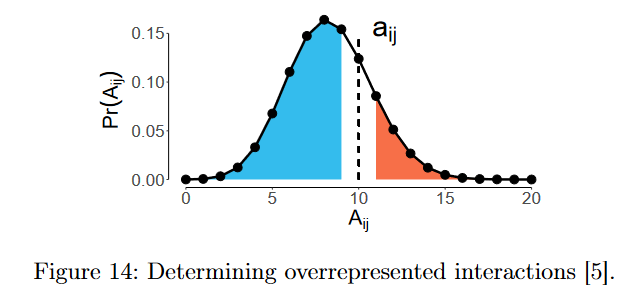

社会组织动态性

社会组织网络必须考虑组织成员的进入和退出，这些节点及其边不是随机的。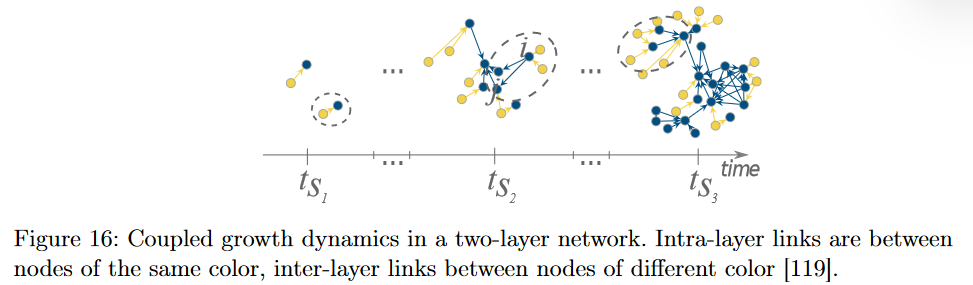

紧随着节点和边的增减变化的是网络连接的重构，结构变化通常反映了组织的变化。

网络动力学变化改变了其拓扑结构，这些动态变化捕获了Agents之间的互动关系。这一过程是高度路径依赖的，满足时序和因果关系。我们可以构建高阶网络，每一阶捕获给定路径的因果路径，实现因果路径建模。

时序网络反映了活动的突发性，网络中并非所有的边在任何时间上都是活跃的。时间成分对单个Agent的中心性衡量有显著影响。中介中心性偏好作为Agent中心的信息传递重要性量化。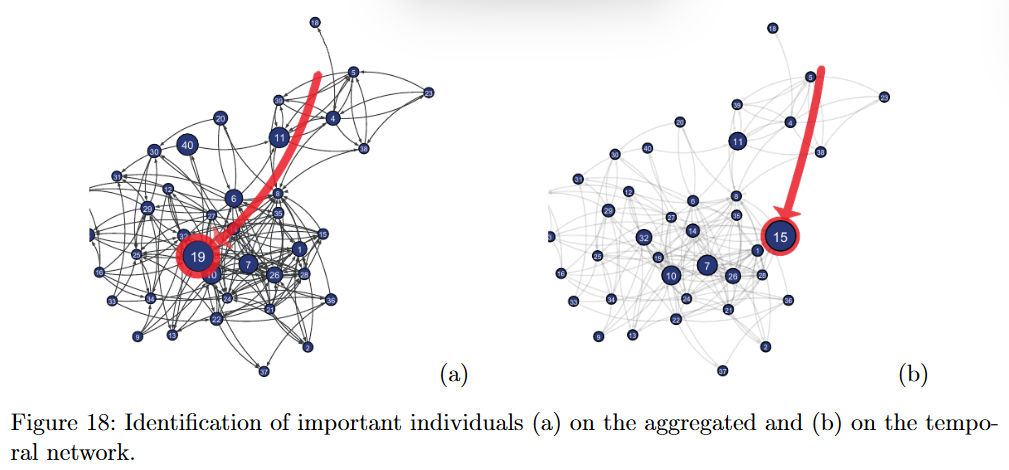

组织网络的动态性刻画了内外部冲击的规模和起点，例如内部冲击可能导致Agents脱离网络，并引发级联和重构；外部冲击会改变工作条件和协作关系。

韧性计算

• 操作化

Agent量化属性主要包括Agents重要性和Agent社会影响力。

Agents拥有不同重要性$r_i$反映了他们的社会地位、声誉、组织关系、知识等。作者指出有向网络的一种可能量化方法是使用Agents特征向量的中心度衡量，而无向网络使用coreness或加权k-core中心度量化。

对于时序网络中介中心度可以量化Agent重要性，Agent的功能性角色只能通过社区模式或特殊的Agents拓扑嵌套进行部分推断。

个体社会影响力为$I_i=\sum\limits_jw_{ij}r_j=I_i^p-I_i^n$，其中$w_{ij}$为Agents之间的关联的权重和方向，$I_i^p$为所有正向关系之和，$I_i^n$为所有负向关系之和。而个体的总影响$q_i=r_i+I_i$，即自身重要性和社会影响之和。

作者认为拓扑鲁棒性只能通过特定冲击来衡量。对Agent脱离的鲁棒性可以通过Agents的coreness关联表示，移除特定Agent有助于分析级联效应。集中化反映了互动主要集中在少数Agents之间，当失去这些Agents时系统风险会上升。中介中心度偏好和Eigengap反映了通讯瓶颈及识别守门员。

作者将网络分解为三元结构，并分析其$S_{ijk}$平衡关系来衡量结构鲁棒性。但这种方法分析的三元结构是孤立的，也没有考虑到正负向关系的权重和Agents重要性。作者试图通过新的权重平衡测量来修正这些问题。

韧性$\mathcal{R}(R,A)\sim R\cdot A$表明鲁棒性是双刃剑。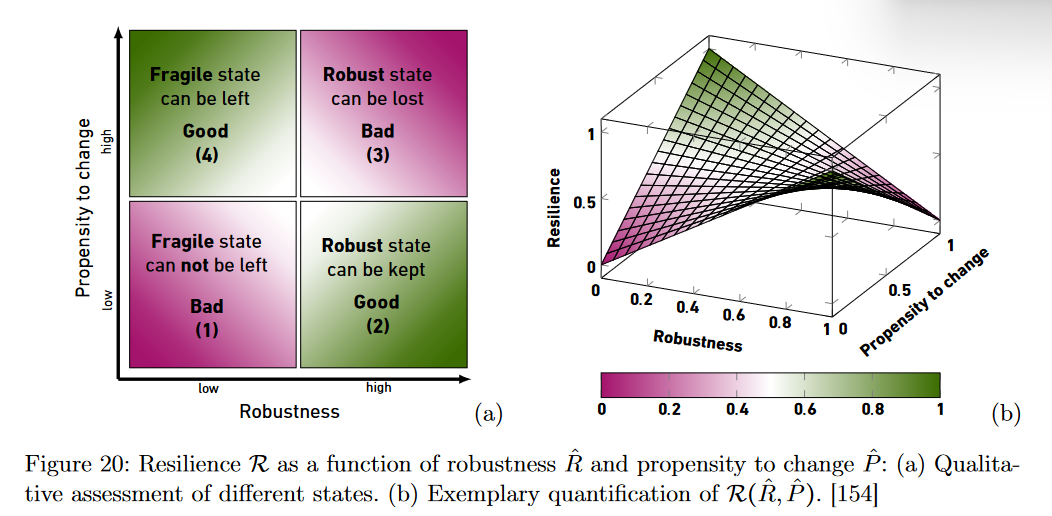

作者将社会组织韧性转化为$\mathcal{R}(\hat{R},\hat{P})=\hat{R}(1-\hat{P})+\hat{P}(1-\hat{R})$，使用代理变量进行测量。

网络构建和干预

• 数据收集
• 交互提取
• 时间窗检测
• 时序数据分析
• 网络回归
• 校准和验证

干预措施干货不多，比较有趣的一点是可以通过多层网络拆解社会组织关系，从特定组织关系类型识别合适的Agent节点进行干预，还有移除部分节点可以增强组织的韧性。

• Previous
  【阅】本周阅读摘选2023-02-20 → 2023-02-26
• Next
  【阅】本周阅读摘选2023-03-06 → 2023-03-12