日常 复杂科学 数智化营销 消费者行为 仿真与决策

【阅】本周阅读摘选2023-03-13 → 2023-03-19

Posted by Cao Zihang on March 21, 2023 Word Count:
本周阅读摘选
2023-03-13 → 2023-03-19
目录

学术相关

Nat. Neurosci. 速递：社交网络中实时分布式学习的神经计算机制1

基于人口流动-引力耦合协调的同城化测度方法及优化策略——以武汉大都市区为例2

品味区分、享乐欲望与亲密关系：当代消费社会学三题3

本文综述了自上世纪80年代以来，布尔迪厄的《区分》（品味区分）、坎贝尔的《浪漫伦理与现代消费主义精神》（享乐欲望）和泽利泽的多本专著（亲密关系）这三大消费社会学取向的代表作，对后续如何围绕这三个命题进行理论和经验的重建。

消费社会学最早在1976年由商科学者《迈向消费社会学》一文中出现，但社会学直到1983年仍然只有“消费者”的概念，并解释为经济学的供需关系，在80年代后，社会学对消费的关注才开始快速发展。

从发展历程上看，消费社会学具有较强的跨学科属性，代表作品如《牛津消费研究手册》（Oxford Handbook of Consumption）和《劳特里奇消费研究手册》（Routledge Handbook on Consumer）。

基于《劳特里奇消费研究手册》主编Keller的说法，消费社会学第一阶段关注的是消费行为背后的社会与文化范畴；第二阶段是消费活动的表达形式与文化动力；第三阶段是消费品物质技术面向和日常生活实践面向。

  • 品味区分命题——布尔迪厄（法·1930~2002）
    • 聚焦时空：法国20世纪60至70年代
    • 消费品味是社会群体分层之间差异甚至厌恶的体现

布尔迪厄以《区分：判断力的社会批判》一书为代表，推动了“品味”的文化实践研究，使之成为该研究的主流核心概念。布尔迪厄认为，社会是一个以消费品位或习性形成的区分性空间，这个空间划分出不同的社会阶层，体现为人们所拥有的差异化消费品位。

  • 批判经济学对消费研究的问题
    • 经济学只关注物品的有用性，因而不加区分地理解物品的价值。
    • 没有关注消费群体内部的异质性
  • 将消费从经济维度延伸至文化维度
    • 消费体现品味
      • 偏好&厌恶
      • 同类群体集合；异类群体阻隔
  • 消费品味体现的社会阶层区分
    • 基于资本总量、资本构成（文化资本、经济资本比例）及两种资本的社会轨迹变化三个维度
    • 较高的社会阶层将自身作为合法性文化，在三个维度空间的高低区分上具有批判性，使被统治阶层只能作为陪衬，既向上承认和追求高等的消费品味，但又由于阶层所限而使自己的消费品味智能处在边缘
  • 重点分析文化消费（图书、音乐）、食物消费、外观消费（衣服、运动）三个方面的消费社会学
    • 食物消费
      • 资本总量：较高社会阶层人群消费精致、清淡的食物，鄙视较低社会阶层人群以高热量、增肥食物为主的饮食习惯
      • 资本构成：具有较多文化资本但经济资本较少的群体重视稀有食物，具有较少文化资本但较多经济资本的群体重视丰盛度
      • 社会轨迹
        • 品味继承

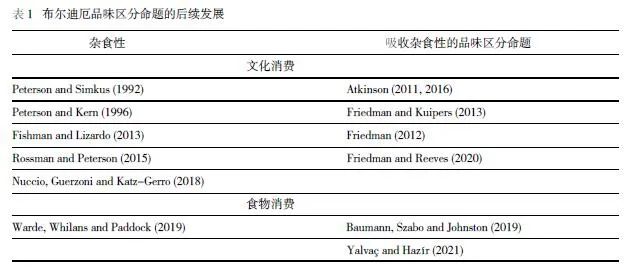
对布尔迪厄观点最有代表性的反驳是美国文化社会学家Richard Peterson的“杂食性”观点。他们批判布尔迪厄的研究对象处于20世纪60~70年代具有贵族传统的法国，而不适用于其他国家和时段。该观点认为布尔迪厄将社会阶层成员看做单一品味的势力者，但美国较高社会阶层成员实际上是杂食主义者，他们不仅消费该阶层的文化象征产品（古典音乐等），也消费属于较低社会阶层的文化产品（如摇滚音乐）。

Peterson通过美国公众艺术参与的多轮调查数据（1982-）发现，美国较高社会阶层群体中，只有约30%会偏好古典音乐，他们也会喜欢消费乡村和摇滚等通俗音乐。也有人从历史中寻找杂食性现象，如19世纪初意大利的古典音乐乐谱销售记录，指出消费古典音乐的原因更多取决于一个人过去的消费历史，而非阶层。

这些研究大多假设品味的对象是一成不变的，而不受环境的影响，这正确吗？另外，是否杂食及消费比例真的能代表品味吗？或者说测量的校标是什么呢？现实阶层与期望阶层是否进行了区分呢？

杂食主义消费品味，蕴含着开放、平等与包容的意涵，又是布尔迪厄研究的反命题，因而不管是从现实旨趣还是从学术旨趣来看都受到学界欢迎。

布尔迪厄主义者对杂食主义者观点进行了批判。其一，杂食主义者没有真正验证布尔迪厄概念框架，布尔迪尔的概念中不仅有资本总量，也有资本构成和资本的社会轨迹，而杂食性研究在量化分析中仅关注了资本总量（基于收入的经济总量和基于教育水平的文化资本），完全忽视了资本构成和资本的社会轨迹。其二，从品味区分作为反向的厌恶而非正向的偏好角度，布尔迪厄命题能够解释为什么消费品位看似杂食，但实际上背后也有品味区分的蕴涵，而杂食主义者只测量了偏好。其三，杂食主义者忽视了底层群体，且精英群体的杂食性消费也是高度选择区分的结果，只有精英才能通吃高雅与通俗文化。

img

  • 享乐欲望命题——柯林·坎贝尔（英·1940-）
    • 聚焦时空：英国18世纪
    • 现代消费是为了追求享乐幻想的欲望感，而非填补匮乏的满足感

坎贝尔的《浪漫伦理与现代消费主义精神》一书提出的享乐欲望概念引发巨大反响。他认为消费主义精神的现代模式不是基于感官与物品匮乏下的需求满足，而是在欲望引导下出现既获得又幻灭的交织性。

  • 现代消费社会实际兴起于18世纪英国工业革命
    • 同期，英国诞生了休闲主义的思潮与运动，流行时尚发端
    • 浪漫与休闲消费反映了当时新兴消费力量——中产阶级的生活
  • 与传统消费主义相比，坎贝尔认为现代精神下的消费是有规律且永无止尽地生产想要更新产品或服务的欲望。
    • 这种欲望是以享乐为导向的
    • 追求体验，需要持续刺激；
    • 快乐源自产品的象征意义带来的想象式享乐，当拥有变成现实时，会产生幻灭感，进而再生产并追求进一步的欲望
    • “欲望—获得—使用—幻灭—更新—欲望”循环
  • 坎贝尔的解释逻辑为当时时尚消费的享乐欲望找到18世纪的艺术与宗教思潮推动的浪漫伦理这一正当理由。
    • 坎贝尔认为在为资本主义生产提供伦理正当性支持的加尔文教之后的新教教义和资本主义关系，使宗教的生产伦理正当性转向了消费伦理的正当性
    • 宗教的合理性席卷了文化艺术领域，形成了一股社会文化变迁的“浪漫主义运动”
  • 坎贝尔指出经济学观点无法解释现代消费主义精神

坎贝尔的观点对消费社会的形成，尤其是时尚消费领域，观点尖锐新奇，对学界很有冲击力。

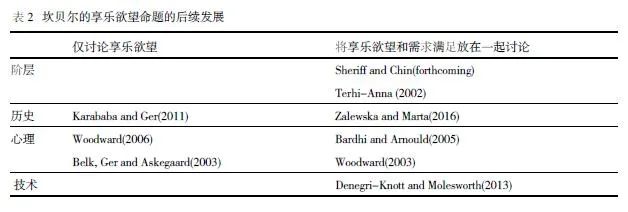
但在消费社会学实证研究中，坎贝尔的享乐欲望理论毁誉参半。一方面，它深刻揭示了当代时尚消费现象；另一方面，人们批评它不足以概括所有行业、地区甚至消费者的文化与动机，尤其是坎贝尔激进地建立了满足需求（前现代消费主义精神）与享乐欲望（现代消费主义精神）的二分法，引发诸多批判。

Terhi-Anna通过芬兰数据量化研究反驳了坎贝尔的观点，她认为坎贝尔将欲望变得过于一般化了，反而不合实际，需要分类讨论。其他学者也有类似的发现，他们认为不同阶层群体会有不同的享乐欲望想象，导致消费取向可能同时将享乐与理性需求纳入。

从互联网时代的技术视角，Denegri-Knott & Molesworth批评坎贝尔的理论忽视了当前消费场景中的技术镶嵌情况，他们进一步指出，消费欲望是人类-软件混合体。如今，软件承担寻找消费者的任务，但软件既会唤起消费者的欲望和想象，也会使欲望变得更加有利于管理，反而让人们转向需求满足的实用目的。

img

  • 亲密关系命题——泽利泽
    • 聚焦时空：美国19世纪中叶至20世纪上半叶
    • 消费不仅仅是市场商品化行为，也是日常生活交叉至亲密关系领域，具有道德神圣化的逻辑

泽利泽从经济社会学进入消费社会学领域，她批评了经济社会学对消费研究漠不关心的问题。她聚焦于私人生活的亲密关系，消费活动不再是利益最大化与理性标准同质化的经济活动，而是经济与社会文化共同影响下的交叉生活。亲密关系的人际作用与道德属性直接影响人们对消费内容的理解。泽利泽要解释的经济学领域核心概念，关注紧密关系的商品化效应和对商品的神圣化与道德化效应。

WWW’23「美团」用于点击率预测的深度行为路径匹配网络4

作者设计了一种用户行为路径表示，并通过深度神经网络将用户当前的行为路径与历史行为路径相匹配，进行行为预测，该模型最终被集成在美团外卖的推荐算法中。但我觉得实验结果上提升并不是很大。

Code

美团外卖APP在运行中发现用户决策心理非常重要，但是现有的CTR预测算法即使考虑到历史行为，也是通过历史行为序列进行候选的点对点激活，没有考虑过包含用户决策轨迹的序列行为的影响。

建模用户行为路径存在3大难点：行为路径稀疏性、行为路径中的噪声干预和路径间精确匹配。

  • 稀疏性：对单一用户，他与APP的互动在个体行为层面并不完整，因此难以捕捉用户的所有行为模式，因此作者采用了对比学习技术对行为路径进行增强。
  • 噪声：随意点击等行为。作者构建了动态激活网络聚焦于路径中的主要行为。
  • 匹配：作者构建了二级匹配机制。第一级计算历史行为路径的激活权重，并选取top-k最似历史路径。第二级，对给定候选路径，计算点击行为激活权重来预测CTR。

用户行为序列

令$\mathcal{U}$为用户集，对于每个用户$u\in\mathcal{U}$的行为序列$s$由按时序的行为$b$组成，即$s=[b_1,…,b_T]$。基于美团外卖场景，每个行为包含交互项目ID、行为类型、发生时间与当前时间差和序列相对位置。美团设计的行为类型包括点击、收藏和下单。

用户点击序列

在用户行为序列$s$中存在大量点击行为，因此可以从中提取子集点击序列$s^c=[b_1^c,…,b_t^c]$。

用户行为路径

对用户点击序列$s^c$中的第$i$个点击行为$b_i^c$，令$b_{m(i)}$为行为序列$s$中的$b_i^c$的相关行为，则关于点击行为$b_i^c$的用户行为序列为$p_i=[b_{m(i)-l},…,b_{m(i)-2},b_{m(i)-1}]$。

作者的概念操作化方式使得点击行为和行为路径一一对应。

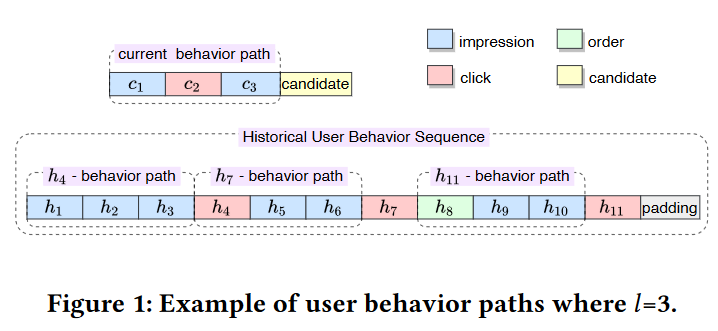
image-20230429215902099

示例中包含3个用户行为路径（每条路径预设长度为3）。

行为路径序列

行为路径$s$中所有用户行为路径$p_i$组成的集合$P=[p_1,…,p_l]$为行为路径序列。

  • DBPMaN 模型
    • Embedding Layer
    • PEM (Path Enhancing Module)
    • PMM (Path Matching Module)
    • PAM (Path Augmenting Module)

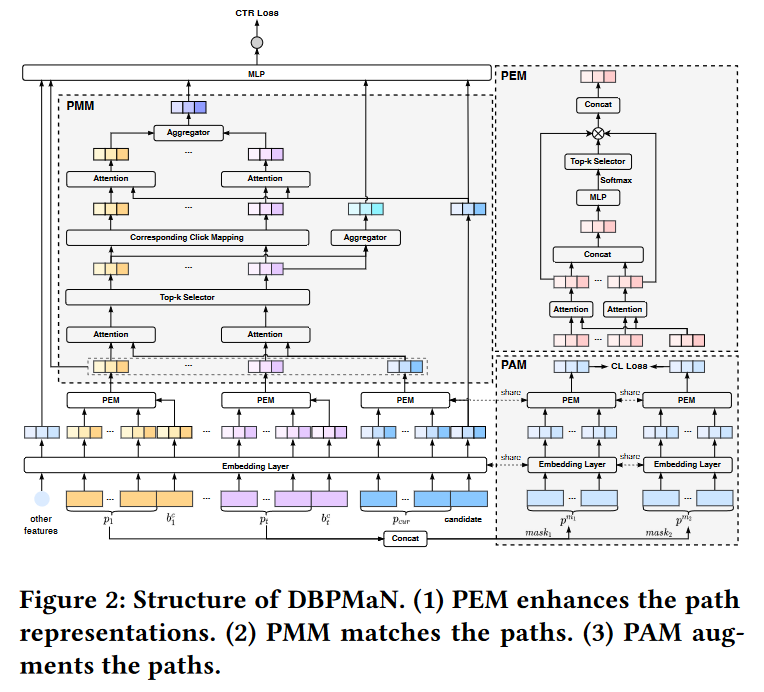
image-20230429220443168

DBPMaN模型输入包含项目配置（项目ID和类别、地点、评分等边信息）、用户配置（用户ID和年龄、性别、城市等边信息）和用户行为序列中的行为信息。这些数据被喂进Embedding层，之后对每类特征使用SUM Pooling提取特征，计算用户行为序列Embedding $s=[e_1,…,e_T]$，用户Embedding $e^u$，候选项Embedding $e^{ct}$。

作者认为用户行为路径中的不同行为对下一次点击的发生有不同的贡献，因此设计了PEM来挖掘这一信息。给定的每个Embedding行为路径及其点击行为，PEM首先激活路径中的重要行为，之后优化路径时期更精准。之后，PMM利用当前Embedding行为路径和历史行为路径作为输入，寻找$k$个最似历史行为路径，并激活相关的$k$个点击行为作为候选。

此外，作者使用了PAM增强了数据，作者mask每个历史行为路径来获取2个增强路径，并喂入Embedding层和PEM，通过InfoNCE损失作为对比损失，将源自相同行为路径的Embedding拉近。

DBPMaN模型使用负对数似然函数作为主损失函数，目标函数是主loss和对比loss的组合。

  • PEM

对用户行为路径应用局部激活单元， 执行一个加权concat池化，自适应地计算行为路径Embedding。

$\begin{aligned}e_{m(i)-j}^{te}&=a(e_{m(i)-j},e_i^c)\cdot e_{m(i)-j},\ 1\leq j\leq l\\ s_{i}^{te}&=[e_{m(i)-l}^{te},…,e_{m(i)-2}^{te},e_{m(i)-1}^{te}]\\ p_i^{te}&=concat(s_i^{te})\end{aligned}$

其中$a(\cdot)$为多层感知机，它的输出作为第一层激活分数。

之后将$p_i^{te}$喂入另一个使用Softmax激活函数的多层感知机，学习行为路径上每个行为的第二层激活分数。

$score_i=softmax(MLP(p_i^{te}))$

最终的$score_i$为$l$维向量，之后选取top-k分数并与其$s_i^{te}$中对应的行为Embedding相乘。通过连接按分数缩放的Embedding，我们得到了增强的路径Embedding $P_i^e$。

最终的增强路径Embedding序列为$P_e=[p_1^e,…,p_t^e]$。

PMM

目的是寻找前$k$个与当前路径最似的行为路径，之后获取对应的$k$个点击行为。

给定增强历史路径Embedding $P_e=[p_1^e,p_2^e,…,p_t^e]$和增强当前行为路径Embedding $P_{cur}^e$，作者将$p_i^e\in P_e$和$P_{cur}^e$喂入一个得分门单元获取相似分数$g_i^p=MLP(concat(p_{cur}^e,p_i^e,p_{cur}^e\otimes p_i^e))$。在相似得分列表$g^p=[g_1^p,g_2^p,…,g_t^p]$中，选取最高$k$个得分，其对应的点击行为Embedding为$s_e=[e_{c_1},…,e_{c_k}]$。之后，对选择的路径Embedding与对应的得分相乘获取调整Embedding $E^p=concat(Filter(g^p,[g_i^p\cdot p_i^e,1\leq i\leq t],k))$。

之后，作者使用同样的方法计算候选和点击行为之间的相似分数获取用户兴趣的表示向量。$g_i^c=MLP(concat(e^{ct},e_{ci},e^{ct}\otimes e_{ci})), E^c=concat([g_i^c\cdot e_{ci}, 1\leq i\leq k])$

最后，串联$P_e, E^p, E^c, e^u,e^{ct}$并喂入MLP层，输出预测CTR。

实验结果

作者使用了淘宝和美团外卖两个产业数据集测试模型。离线实验度量用AUC、RelaImpr，线上实验使用CTR和CPM度量。

  • 离线实验结果

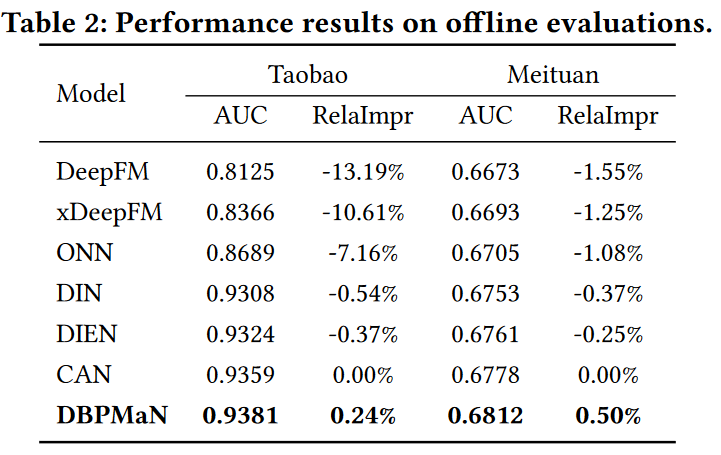
    image-20230501211504731

  • 消融实验

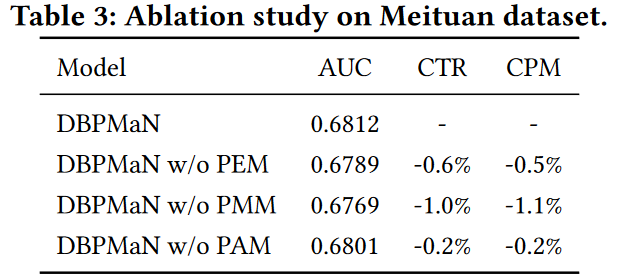
    image-20230501211526069

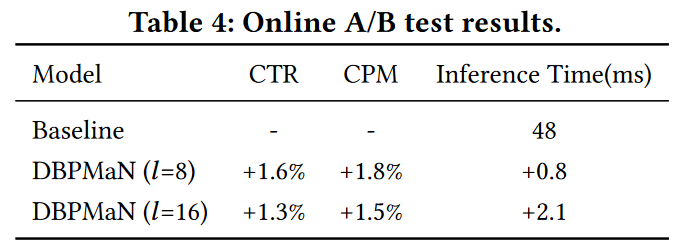
  • 在线AB测试结果

    image-20230501211550875

NIPS「Intel」多任务学习中的多目标优化问题5

Code

Stein悖论表明使用所有样本同时估计3个或以上的高斯随机变量均值，比分别估计效果要好，即使这些高斯分布是独立的。Stein悖论是MTL的早期动机，即利用一个学习范式，使用多任务数据期望获取超额表现。然而，MTL的潜在优势要超过Stein悖论的直接影响，因为两个看似无关的真实世界任务，由于产生数据存在共享过程，也会有很强的依赖性。例如自动驾驶和目标操作看似无关，但由于相同的光学规律、材料属性和动力学都对数据产生有影响，所以仍然可以通过MTL提升。

传统的MTL使用线性组合构建目标函数，但只有存在一个对所有任务都有效的参数集时，线性组合才是有效的，而这在实践中很少见。MTL的另一个目标是寻找帕累托最优（多目标优化）的方案，本文就致力于寻找这样的方案。

目前存在多种目标优化算法，其中一种是multiple-gradient descent algorithm (MGDA)，它使用基于梯度的优化证明收敛于帕累托集中的一点，可以被很好地应用于MTL。但是MGDA在大规模数据上存在两个技术性问题：底层优化问题不能很好地扩展到高维梯度中；算法需要明确计算每个任务的梯度，导致后续训练时间很长。

本文开发了Frank-Wolfe-based优化器扩展到高维问题。作者通过单一后向传播计算MGDA优化目标的上界，而不计算特定任务的梯度，缩减计算开销。

文献综述

作者主要关注硬参数共享这类MTL。Baxter理论性地分析认为MTL问题是个体学习器和meta算法的交互。即每个学习器负责单一任务，而Meta算法分配权重加总。也有一些算法的Meta部分不仅仅是加权求和，但那些算法均不适用于基于梯度学习的现代深度网络等高容量模型。

多目标优化解决的是优化一组可能矛盾的目标的问题。与本文相关的是使用多目标KKT条件，找到一个能减少所有目标的下降方向的方法。目前，该方法已经被应用于多智能体学习、核学习、贯序决策和贝叶斯优化等领域。本文的目标是在多任务学习中应用基于梯度的多目标优化。

作为多目标优化的多任务学习

考虑一个在输入空间$\mathcal{X}$上的多任务学习问题和任务空间${\mathcal{Y}^t}_{t\in[T]}$，例如一个有大量$i.i.d.$数据点${x_i,y_i^1,…,y_i^T}_{i\in[N]}$组成的数据集，其中$T$是任务数量，$y_i^t$是$i^{th}$数据点的$t^{th}$任务的标签。接着，考虑每个任务的参数假设类$f^t(\mathbf{x};\theta^{sh},\theta^t):\mathcal{X}\to\mathcal{Y}^t$，其中部分参数$\theta^{sh}$的任务间共享，部分参数$\theta^t$是任务特有的。此外，考虑一个基于特定任务的损失函数$\mathcal{L}^t(\cdot,\cdot):\mathcal{Y}^t\times \mathcal{Y}^t\to\mathbb{R}^+$。

前人的研究总体上可以归于生成$\mathop{\min}\limits_{\mathop{\theta^{sh},}\limits_{\theta^1,…,\theta^T}}\sum\limits_{t=1}^Tc^t\hat{\mathcal{L}^t}(\theta^{sh},\theta^t)$，其中$c^t$为每个任务的静态或动态权重，$\hat{\mathcal{L}^t}(\theta^{sh},\theta^t)$是任务$t$的经验损失函数$\hat{\mathcal{L}^t(\theta^{sh},\theta^t)}\mathop{=}\limits^{\triangle}\frac{1}{N}\sum\limits_i\mathcal{L}(f^t(\mathbf{x}_i;\theta^{sh},\theta^t),y_i^t)$。然而，虽然加权求和的方式很符合知觉，但在大规模模型或启发法上网格搜索成本过高，而且有时候难以确定全局最优解。例如，考虑两个解集$\theta,\bar{\theta}$，满足对一些任务$t_1,t_2$有$\hat{\mathcal{L}^{t_1}}(\theta^{sh},\theta^{t_1})<\hat{\mathcal{L}^{t_1}}(\bar{\theta}^{sh},\bar{\theta}^{t_1})$和$\hat{\mathcal{L}^{t_2}}(\theta^{sh},\theta^{t_2})>\hat{\mathcal{L}^{t_2}}(\bar{\theta}^{sh},\bar{\theta}^{t_2})$，在不知道任务相对重要性的情况下，我们无法求解。

作者将MTL公式化为多目标优化，作者采用向量值损失函数$L$: $\mathop{\min}\limits_{\mathop{\theta^{sh},}\limits_{\theta^1,…,\theta^T}}L(\theta^{sh},\theta^1,…,\theta^T)=\mathop{\min}\limits_{\mathop{\theta^{sh},}\limits_{\theta^1,…,\theta^T}}(\hat{\mathcal{L}}^1(\theta^{sh},\theta^1),…,\hat{\mathcal{L}}^T(\theta^{sh},\theta^T))^T$

多目标优化的目的是实现帕累托最优。

定义：MTL的帕累托最优

  • 优势解：当解$\theta$满足对$\forall$任务$t$有$\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)\leq\hat{\mathcal{L}}^t(\bar{\theta}^{sh},\bar{\theta}^t)$且$L(\theta^{sh},\theta^1,…,\theta^T)\neq L(\bar{\theta}^{sh},\bar{\theta}^1,…,\bar{\theta}^T)$，则称$\theta$是$\bar{\theta}$的优势解
  • 当不存在$\theta^*$的优势解的时候，称$\theta^*$为帕累托最优解

帕累托最优解的集合称帕累托集$\mathcal{P}_\theta$，它的图像为帕累托前沿$\mathcal{P}_L={L(\theta)}_{\theta\in\mathcal{P}_\theta}$。

作者针对于大模型和大量任务设计了基于梯度的多目标优化算法。

多梯度下降算法MGDA

针对特定任务和共享参数的KKT条件如下：

  • 存在$\alpha^1,…,\alpha^T\geq0$满足$\sum\limits_{t=1}^T\alpha^t=1$且$\sum\limits_{t=1}^T\alpha^t\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}^t(\theta^{sh},\theta^t)}=0$
  • 对所有任务$t$，有$\bigtriangledown_{\theta^t}\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)=0$

满足KKT条件的点称之为帕累托驻点。所有帕累托最优点都是帕累托驻点，但帕累托驻点未必是帕累托最优点。

考虑优化问题$\mathop{min}\limits_{\alpha^1,…,\alpha^T}{||\sum\limits_{t=1}^{T}\alpha^t\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)||_2^2|\sum\limits_{t=1}^T\alpha^t=1,\alpha^t\geq0\ \forall t}$

表明要么优化问题解为0并满足KKT条件，要么能给出一个改善所有任务的下降方向。

补充

考虑到目标函数展开后，每项都为非负

假设存在两组实数$x_1\leq x_2\leq…\leq x_n$和$y_1\leq y_2\leq…\leq y_n$

$x_{\sigma(1)},…,x_{\sigma(n)}$为$x_1\leq x_2\leq…\leq x_n$的一个排列

则有$x_1y_1+…+x_ny_n\geq x_{\sigma{1}}y_1+…+x_{\sigma(n)}y_n\geq x_ny_1+…+x_1y_n$恒成立

因此，目标函数最小化意味着梯度范数越大的任务权重越小，反之亦然。

优化问题求解

首先考虑2个任务的情况，待优化问题可以定义为$\mathop{min}\limits_{\alpha\in[0,1]}||\alpha\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}}^1(\theta^{sh},\theta^1)+(1-\alpha)\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}}^2(\theta^{sh},\theta^2)||_2^2$，其中，$\alpha$具有解析解$\hat{\alpha}=[\frac{(\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}}^2(\theta^{sh},\theta^2)-\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}}^1(\theta^{sh},\theta^1))^T\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}}^2(\theta^{sh},\theta^2)}{||\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}}^1(\theta^{sh},\theta^1)-\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}}^2(\theta^{sh},\theta^2)||_2^2}]_{+,_T^1}$，其中$[\cdot]_{+,_T^1}$表示对$\alpha$的取值限制在$[0,1]$。

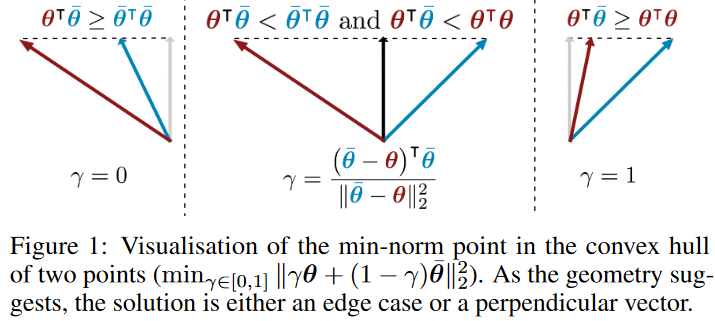
image-20230503174546107

虽然这一解析解仅适用于$T=2$，但由于线性搜索可以被解析，我们可以有效地应用Frank-Wolfe算法来解决约束优化问题。

MTL的更新方程如下：

image-20230503181235009image-20230503181256871

Encoder-Decoder框架下的高效优化形式

Frank-Wolfe解法是有效和准确的，然而由于该算法需要为每个任务$k$计算$\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)$，进而需要对每个任务在共享参数上反向传播。因此，产生的梯度计算先前向传播，然后在$T$上反向传播。考虑到反向传播的计算成本很高，因此对较多任务的问题来说训练成本会比较高昂。

因此，作者提出优化目标上界的替代方法，它仅需单个反向传播。它可以被定义为$f^t(\mathbf{x};\theta^{sh},\theta^t)=(f^t(\cdot;\theta^t)\circ g(\cdot;\theta^{sh}))(\mathbf{x})=f^t(g(\mathbf{x};\theta^{sh});\theta^t)$，其中$g$表示所有任务共享的表示函数，$f^t$是该表示法作为输入的任务特有函数。定义表达$\mathbf{Z}=(z_1,…,z_N)$，其中$z_i=g(\mathbf{x}_i;\theta^{sh})$，利用链式法则和柯西不等式得到上界$||\sum\limits_{t=1}^T\alpha^t\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)||_2^2\leq||\frac{\partial \mathcal{Z}}{\partial\theta^{sh}}||_2^2||\sum\limits_{t=1}^T\alpha^t\bigtriangledown_\mathbf{Z}\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)||_2^2$。$\bigtriangledown_\mathbf{Z}\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)$可以通过单次反向传播计算，$||\frac{\partial \mathcal{Z}}{\partial\theta^{sh}}||_2^2$与权重$\alpha$无关，因此在优化中可以移除。

通过上界替代$||\sum\limits_{t=1}^T\alpha^T\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)||_2^2$获取近似优化问题，并丢弃$||\frac{\partial \mathcal{Z}}{\partial\theta^{sh}}||_2^2$项。最终优化问题为$\mathop{min}\limits_{\alpha^1,…,\alpha^T}{||\sum\limits_{t=1}^T\alpha^t\bigtriangledown_{\mathbf{Z}}\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)||_2^2|\sum\limits_{t=1}^T\alpha^t=1,\alpha^t\geq0\ \forall t}$，即MGDA-UB算法。

作者证明了MGDA-UB算法在弱假设$\frac{\partial\mathcal{Z}}{\partial\theta^{sh}}$满秩下能够产生帕累托最优解。

  • 定理1：假设$\frac{\partial\mathcal{Z}}{\partial\theta^{sh}}$满秩。若$\alpha^{1,…,T}$是MGDA-UB的解，则以下必有一个成立
    • $\sum\limits_{t=1}^T\alpha^t\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}}(\theta^{sh},\theta^t)=0$且当前参数为帕累托最优
    • $\sum\limits_{t=1}^T\alpha^t\bigtriangledown_{\theta^{sh}}\hat{\mathcal{L}}(\theta^{sh},\theta^t)$为所有目标下降的梯度方向

弱假设是非常合理的，因为若矩阵为奇异矩阵，则任务间存在线性相关，没有权衡的必要。

该框架计算开销很低，并且可以应用于任何具有Encoder-Decoder框架的深度多目标问题。

实验结果

  • 基准模型

    • 均匀加权损失函数
      • $\frac{1}{T}\sum\limits_t\mathcal{L}^t$
    • 单一任务模型
    • 网格搜索权重
      • $\frac{1}{T}\sum\limits_te^t\mathcal{L}^t$
    • Kendall 不确定权重多任务模型
    • GradNorm 标准化权重多任务模型

  • 检验问题

    • MultiMNIST

      • Sabour方法 多张图片重叠

        • 识别顶部图片数字
        • 识别底部图片数字

      • LeNet架构

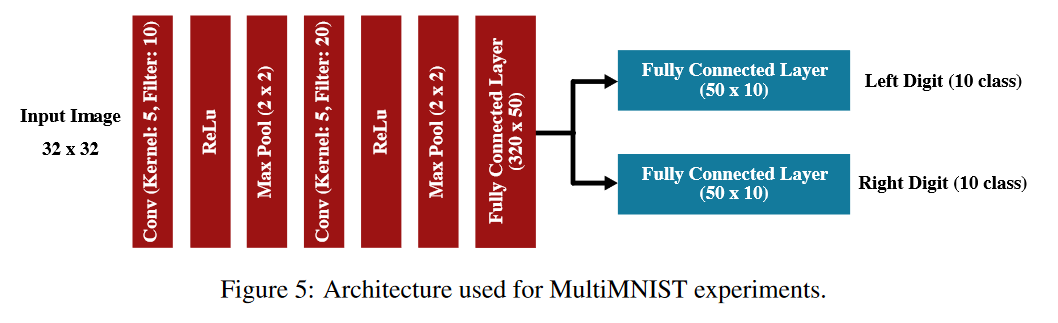
        image-20230503223022715

      • 结果

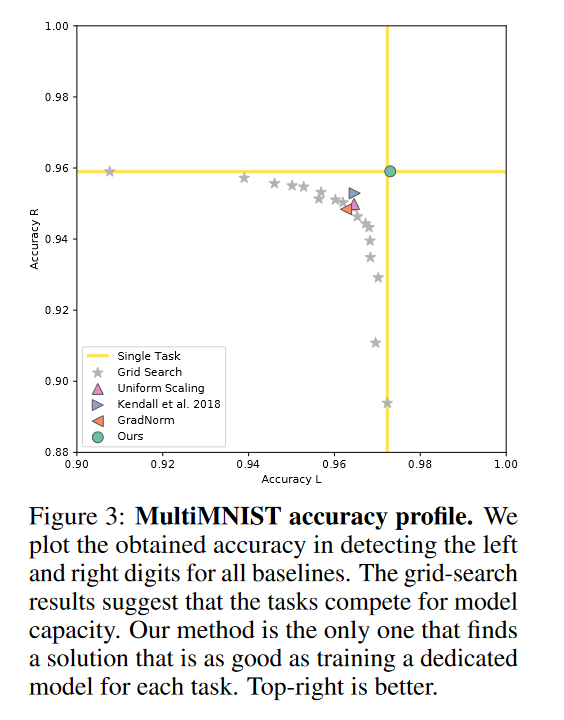
        image-20230503222856919

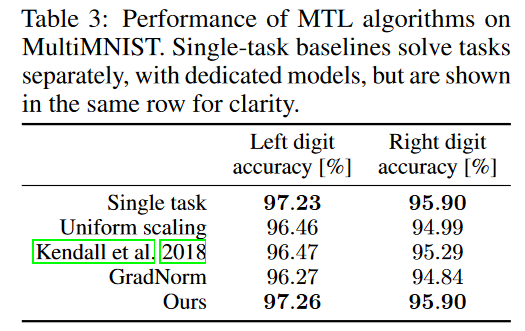
        image-20230503222924647

    • CelebA

      • 问题

        • 40个二分类问题

      • ResNet-18架构

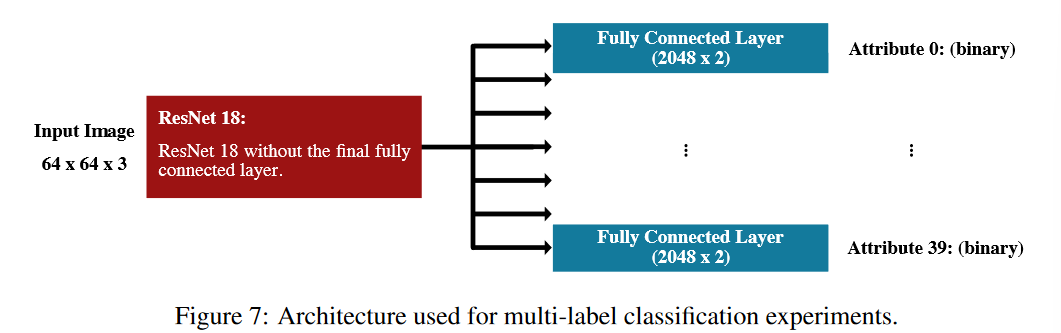
        image-20230503223457727

      • 结果

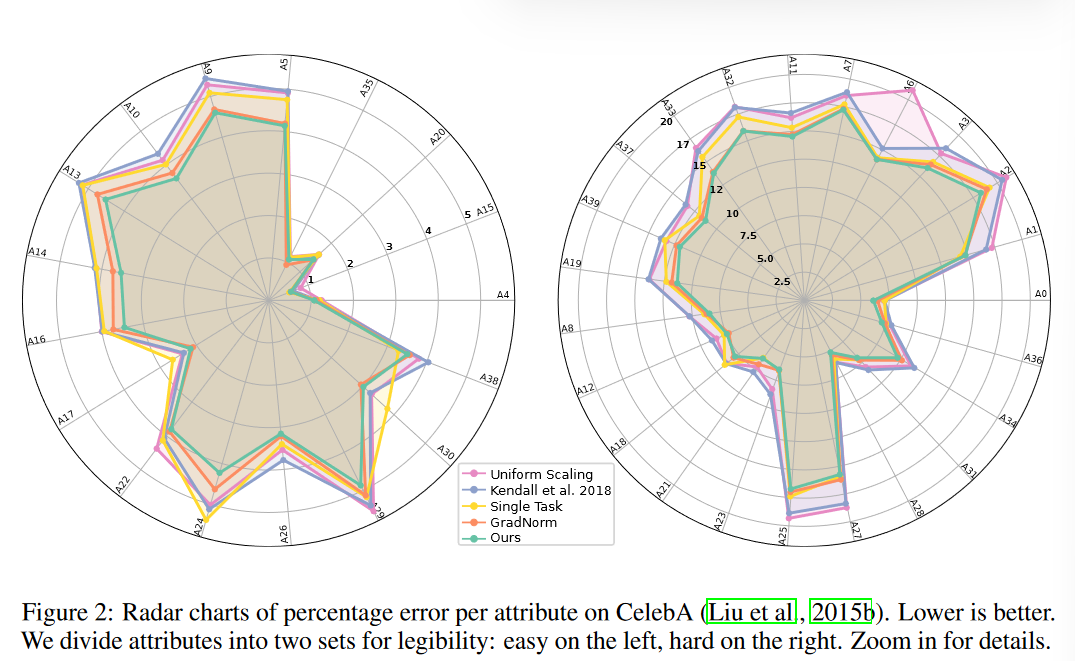
        image-20230503223723788

        image-20230503223638032

    • Cityscapes

      • 场景理解

        • 语义分割（像素级分类标签）
        • 实例分割（像素级实例标签）

      • Encoder-Decoder框架

        • Encoder：ResNet-50

        • Decoder：金字塔池化模型

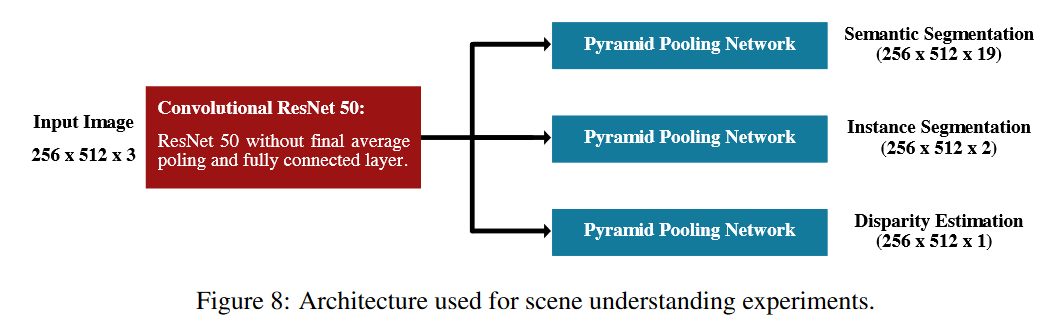
          image-20230503224324310

      • 结果

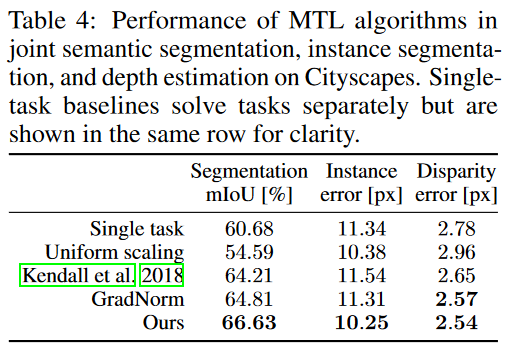
        image-20230503224257212

ABM丨基于 ABM 的公共政策仿真研究进展与方法论启示

ABM近年的快速发展和应用普及开启了社会科学仿真时代，人们可以使用ABM方法进行描述、解释、阐释理论和预测等研究。公共政策领域典型的ABM是复杂适应系统CAS。

一些学者误以为ABM是定量方法，由此使用ABM进行假设检验。然而，虽-然ABM通常基于特定假设，但它不能演绎地得到对某一理论的证明，它的价值在于以仿真实验的方式生成定量可供分析的数据。这些数据源自一系列事先设定的“规则”，用于辅助人们的知觉推理。

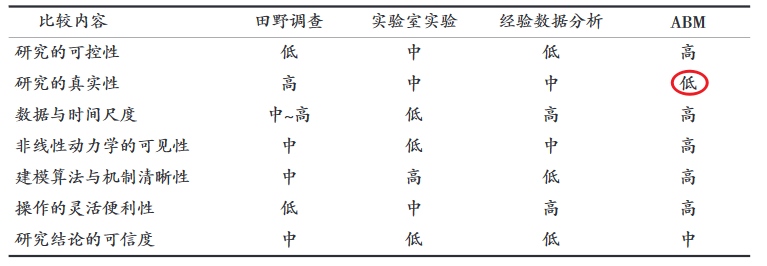
image-20230426161927668

1996年，美国Sandia国家实验室Basu等人研制了基于微观主体的全美经济微观模拟系统ASPEN模型，最初被用于分析经济周期波动线性，随后被扩展到财政政策和货币政策等作用机制及政策效应仿真实验研究，成为ABM经济政策研究的先河。

2006年，欧盟启动宏观经济与政策仿真项目EURACE，旨在构建一个超大仿真模型反映和刻画欧盟经济体的真实运作过程，并搭建税收、福利政策等仿真平台。

目前，虽然ABM是基于微观主体行为构建的，但迄今将之应用于企业投融资、市场竞争和内部管理等方面的决策和政策分析还较为少见。

数智化时代公共政策研究

  • 社会经济的数字化转型
  • 主体行为的数字化精细刻画（从同质性走向异质性）

目前，基于ABM的公共政策研究主要局限于对单一目标政策效应进行分析和评估，或将各政策效应简单分离，不能满足描述复杂问题能力的要求。

早期的ABM研究由于受到计算能力和仿真技术限制，往往局限于KISS（Keep It Simple， Stupid）准侧，这些基于理论驱动的仿真模型仅注重理论思想的体现，不能同真实观测数据关联。

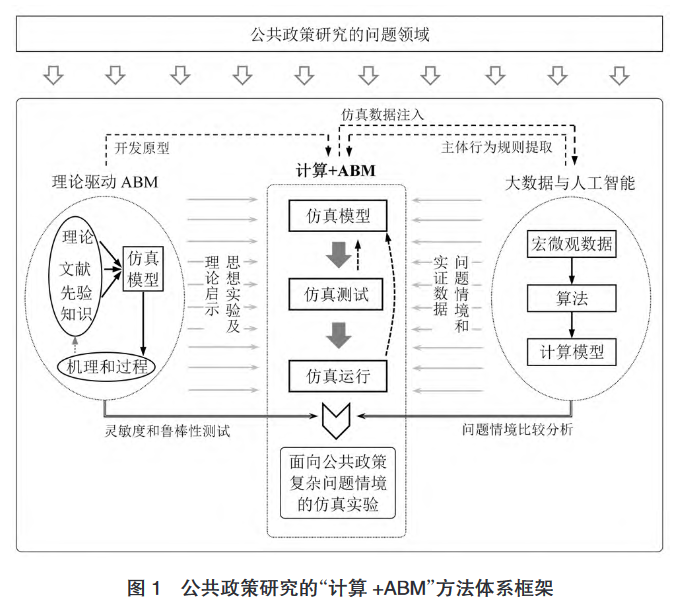
image-20230426164341842

作者提出了一个方法体系框架，可以看出给领域的学者在各自学科的智能决策发展设计上有较高的一致性。

作者同时指出，该框架有两个关键点：

  • 仿真模型的有效性验证和可信性评估
  • ABM和仿真伦理

知识图谱技术体系总览

之前其实一直没有特别关注知识图谱方面的技术，但是现在觉得至少应该有些基本的了解，正好DataFun圆桌写了个概述。突然发现其实以前接触过一点点。

知识图谱技术是知识生产、知识表示储存和知识应用等众多技术的总和。它几乎与所有人工智能细分领域都有交叉，是综合性极强的领域，被认为是当前认知智能的核心研究内容。

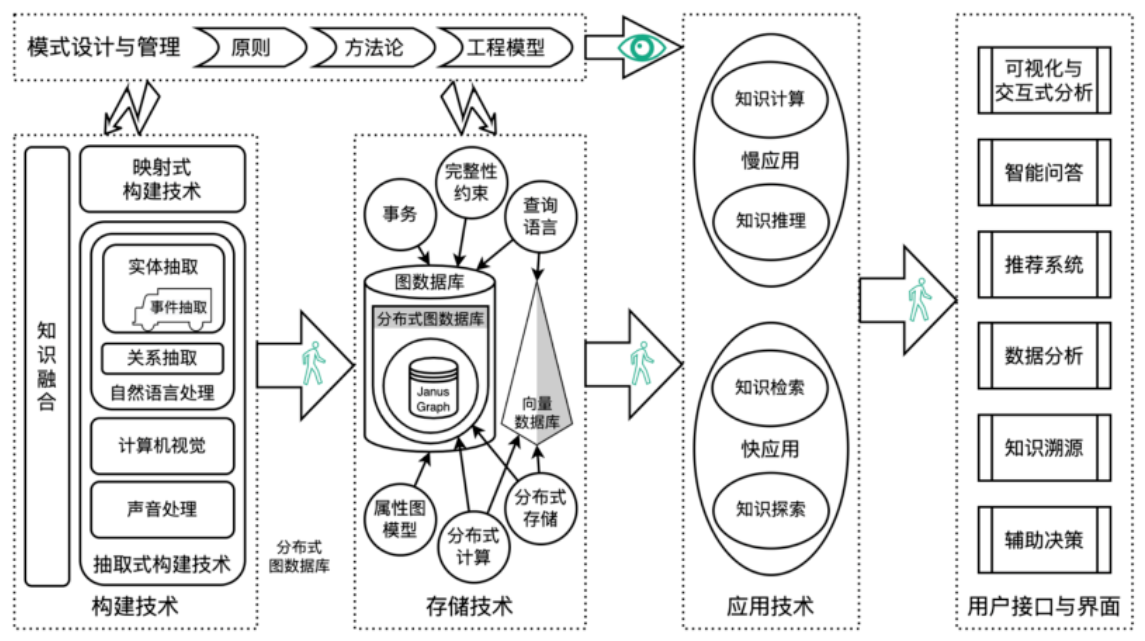
image-20230426153742771

知识图谱构建技术

知识图谱模式Schema

定义知识图谱对知识概念化的一种规范表达。

知识抽取

结构化数据——映射式构建

半结构化数据——实体抽取、关系抽取等知识抽取

实体抽取是知识抽取中最基础的环节，在NLP中称命名实体识别。

img

关系抽取为实体之间建立关联，关系抽取是知识图谱构建中非常困难的环节。常用方法包括基于规则的方法、基于弱监督学习的方法、基于深度学习的方法。目前最为流行的方法是实体-关系联合抽取方法。

事件抽取

事件抽取要提取的内容要素更多，通常包括主题、客体、地点、时间等。常用的方法有先抽取触发词，对触发词分类，进行要素识别的管道模式；一次性把所有要素和主客体触发词识别出来的联合抽取模式。

知识存储技术

图数据库与知识图谱完全契合。目前主流的图数据库包括janusGraph、Neo4j、Dgraph、NebulaGraph。

知识图谱应用技术

知识计算

知识计算是在图论的指导下，使用图论中的定理、推论、模型、算法和相应工具进行计算、处理、分析、理解和挖掘知识图谱的方法。

常见的算法包括路径分析（最短路径、全路径、遍历与查询）、社区分类（模块度、GN、Louvain）、中心性（PageRank、中介中心性、特征向量中心性、亲密中心性）。

知识推理

img

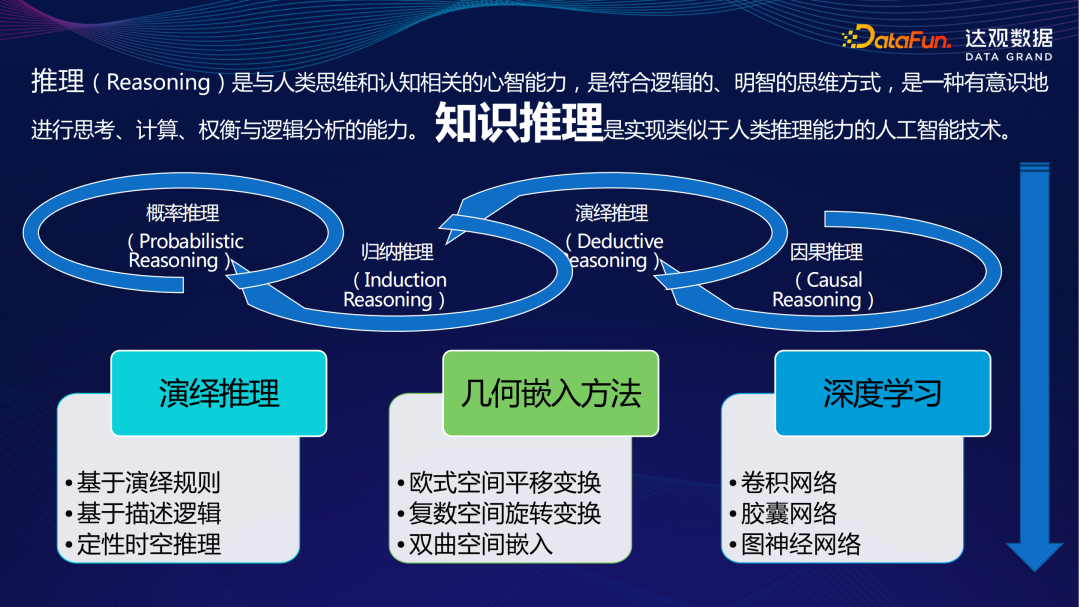
智能问答

使用自然语言提问的方式检索所需知识。

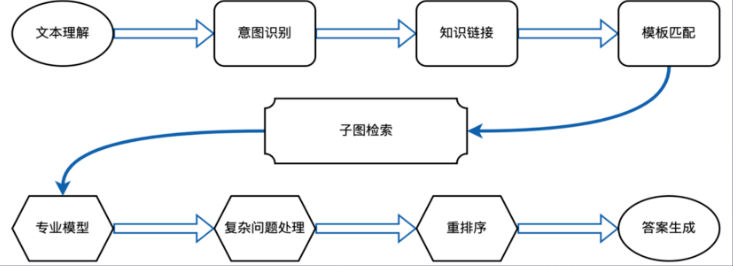
image-20230426160603150

认知推荐

img

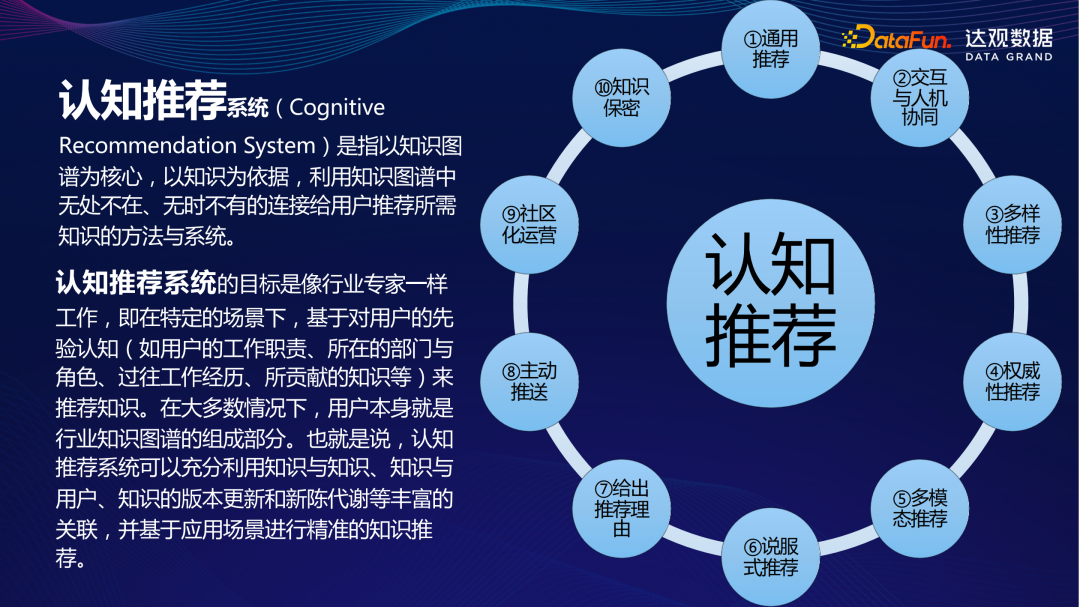
集成时间序列模型提高预测精度

使用Catboost stacking时间序列模型，据说很有用。

技术技巧

Kod：将「代码片段」转换为「漂亮的图片」

从Jupyter里随便找了段古老的代码试了一下，图片可选多种主题，可以设置语法高亮、标题、水印（czh）、背景和模糊行（仍然可见，没多大用）

kod (1)

  1. Jiang, Y., Mi, Q., & Zhu, L. (2023). Neurocomputational mechanism of real-time distributed learning on social networks. Nature Neuroscience. https://doi.org/10.1038/s41593-023-01258-y ↩

  2. Qiang, N., Canhe, Z., Lei, W., & Junbo, Z. (2023). Using coupled people-gravity coordination as a measurement method and optimization strategy for urban integration: Use the Wuhan metropolitan area as an illustration. Transactions in Urban Data, Science, and Technology, 2(1), 39–55. https://doi.org/10.1177/27541231221140714 ↩

  3. 孙宇凡 ↩

  4. Dong, J., Yu, Y., Zhang, Y., Lv, Y., Wang, S., Jin, B., Wang, Y., Wang, X., & Wang, D. (2023). A Deep Behavior Path Matching Network for Click-Through Rate Prediction (arXiv:2302.00302). arXiv. http://arxiv.org/abs/2302.00302 ↩

  5. Sener, O., & Koltun, V. (2019). Multi-Task Learning as Multi-Objective Optimization (arXiv:1810.04650). arXiv. http://arxiv.org/abs/1810.04650 ↩

CATALOG
    FEATURED TAGS
    消费者行为 日常 深度学习 学习笔记 可视化 数智化营销 复杂科学 市场调研 研究方法 世界趋势 仿真与决策 LLMs 数据科学 日常工具 机器学习 资料 AB测试 供应链管理 城市科学 推荐系统