本周阅读摘选 2023-03-20 → 2023-03-26 目录

学术相关

Donoho: 数据科学50年¹

50年前，John Tukey呼吁对统计学进行改革，他指出，在数据分析的未来存在着一门尚未被认识的科学，它的主题是从数据中学习或“数据科学”。

数据科学与统计

许多机构将数据科学定义为“收集、管理、处理、分析、可视化和解释与各种学科、转化和跨学科应用相关的海量异质数据。”

很多统计学家认为他们所从事的工作就是数据科学所描述的工作，实际上也确实是，所以这就令许多人非常困惑。目前，数据科学的教学项目倾向于将统计学边缘化，认为统计学只是数据科学的一部分，但他们又在实质上从事应用统计的工作。许多人认为统计学和数据科学的区分在于数据量大小的问题，但是，虽然在过去的几百年里统计学主要处理小样本推断，但事实上统计学家处理的是数据，无论大小。这导致许多统计学家被困在一个疑惑时刻：几个世纪以来，他们关注的问题成为焦点，但功劳却归功于新星和陌生人（即便数据科学不是他们创造的）。

大数据模因

大数据不是统计学与数据科学的区分标准。

历史上，统计源于于现代人口普查数据编制工作，早在200多年前就已经是大数据了。科学上，数理统计学家一致试图科学地理解大数据。

事实上，数据科学=大数据的框架没有在任何领域识别到本质的东西。

技能模因

计算机科学家通常认为数据科学关注的是传统计算资源无法容纳的大数据，数据科学家需要具备处理此类大数据的技能。作者先前已经驳斥了数据科学=大数据的说法，此处又加上了大数据技能。

在10年代早期，很多人说这是指精通Hadoop《Hadoop: The Definitive Guide. Storage and Analysis at Internet Scale, 4th Edition by Tom White》。但在喧嚣的背后，一个尴尬的事实是其实人们早就有办法完成这些工作，甚至更好。科学家会利用优雅的数学和以数学为模型的强大量化编程环境，发展出解决感兴趣问题的技能，这些环境是基于50多年来不断改进的结果。

吸引媒体关注的新技能不是更好地解决问题，而只是处理大规模集群计算的组织技能。

工作岗位模因

当下，大量大数据岗位被创造，而理论上任何的高级量化学位都应足以胜任这些工作。但今天的大数据项目意味着传统的统计学位并不能进入这些工作岗位——缺少计算机和数据库技能。

Yanir Serousi指出：“没有工作经验的人很难获得真正的数据科学职位。”

由于业务和企业的差别，人们在获取硕士学位后，仍需要多年的打磨技能才能成为数据科学家。数据科学项目实际上并不知道如何满足雇主的需求，它相对于传统的统计学最大的区别就是提供了额外的信息技术培训。然而，这些学生学习到的特定信息技术与用人单位的实际需求却常常不匹配。

相比之下，数据分析和统计更加广泛适用。

作者指出，今天大众媒体对数据科学的理解甚至经不起最基本的推敲。媒体写手和管理者被吓到了，每个人都认为人类事物将产生一个沟通断层。确实，这些年海量的数据被生成，但科学并不会因此而产生新的学科。至少50年来，有远见的统计学家一直在试图构建一个作为传统统计学扩展的数据科学，它不同于被热捧的数据科学，而是聚焦于从数据中学习的科学。

数据分析的未来，1962

1962年John对数据科学的设想震撼了当时所有的统计学家。John Tukey定义了数据科学这门新学科的四个驱动力：统计学形式理论；计算机和显示设备的快速发展；大量领域面临海量数据挑战；越来越多学科强调量化。这意味着统计学只是数据科学的一小部分。数据分析可以从传统统计学中借鉴很多，但必须足够灵活。

1962-2015的50年

John的观点并没有很快得到认可，事实上花了数十年，人们才意识到《数据分析的未来》这篇论文的重要性。在过去的时间里，即使Huber等学者最终追寻了John的观点，但主流的统计学学者仍然持反对意见，反而其他领域的学者更容易接纳John的观点。

1993年贝尔实验室的John Chambers公开发表文章，指出统计学到了面临决策的时间，究竟是采取大口径的从数据中学习还是窄口径的数理统计。此后，不断有学者指出要拓宽统计学口径。2014年Cleveland 提出6项数据科学的焦点，并建议了对应的精力分配：

跨学科调查 25%
数据建模和方法 20%
数据计算 15%
教学法 15%
工具评估 5%
理论 20%

2001年Breiman指出数据分析存在预测和推断两种目标，数据的使用者基于他们的主要目标将数据分析分为两种文化。“生成式建模”文化（Generative modeling culture）寻求建立拟合数据的随机模型，然后根据模型的结构对数据生成机制进行推断。这类文化的基本假设是存在一个真实的模型生成这些数据，并存在一个真实的“最佳”方式来分析数据。Breiman认为98%的学术统计学家都持有这类观点。“预测式建模”文化（Predicative modeling culture）优先进行预测，少数统计学家和许多计算机科学家，特别是工业界科学家持有这类观点。这类建模方式不在乎数据生成的基本机制，允许存在多种预测算法，只讨论预测的准确性。

预测式建模的秘密武器

一般任务框架CTF
- 公开训练数据集：样本、特征、标签
- 一组从训练数据中推断类别预测规则的潜在竞争者
- 评分标准

Liberman 对CTF框架的成功经历做了总结，①错误率每年以一个固定百分比下降，最终达到一个取决于任务和数据质量的渐近值；②进步通常源自微小的改进，1%的变化可能产生极大的成功；③共享数据起到至关重要的作用，并会以出乎意料的方式被重新利用。作者指出：机器学习取得成功的领域基本上否是CTF被系统性应用的领域。

机器学习的成功根本上源自预测式建模文化与CTF框架。简而言之，信息技术是预测模型的核心技能，而非数学。与此同时，开源软件运动也成为它成功的一大要素。

因此，CTF工作所需的技能就具体为下载和有效调整一组脚本。

数据分析的研究设计和应用
探索和分析数据
存储和检索数据
应用机器学习
数据可视化与沟通

更高级的课程包括：

实验和因果推断
应用回归和时间序列分析
数据科学的法律、政策和伦理
大规模机器学习
更大规模的数据分析

更广泛的数据科学

数据收集、准备和探索
数据描述和转换
- 现代数据库
- 数学表示形式
数据计算 (Computing with Data)
- R / Python
数据可视化和展示
数据建模
- 生成式建模 & 预测式建模并行
数据科学的科学
- 元分析
- 横向分析
- 跨工作流分析

而此时数据科学与统计学的区分就变得清晰起来，数据科学在统计学的“数据建模”的基础上增加了“数据表示”和“数据计算”，同时关注预测式建模。

2015-2065的50年

开放科学
科学即数据
- 科学研究中包含大量数据，但目前只能手动获取
科学的数据分析：实证检验

哈佛经济系李光耀孙子做经济学术presentation的经验和建议！

记住知识的诅咒
- 你已经思考这个主题几周（或几个月、几年），但你的听众可能只思考了这个主题几分钟。许多对你来说显而易见的事情对你的听众来说可能并不明显。
- 花时间解释新的概念或不寻常的步骤，即使它们事后看起来微不足道。
教学，而不是辩护
- 作为演讲者，你的工作是帮助听众理解动机、模型和结果，坦率地讨论优点和局限性。
- 模型/结果只是你找到它们的意义，而不是你拥有它们的意义。
- 努力成为关于模型和结果限制方面最具信息量的人。
快速进入模型
- 如果你花费很长时间在动机或模糊的总结上，你的听众会对模型应该如何看待形成强烈的观点，并且当模型与他们预期不同时会感到失望。
- 在模型之前不要先进行文献综述，先说你做了什么。
- 在20分钟的演讲中，不要花费超过3分钟来介绍模型。
PPT
- 有证据表明，声明的可信度受到视觉处理的容易程度的影响。实验对象更可能相信使用高对比度背景显示的声明是真实的，而不是低对比度背景，并且更可能记住使用大字体显示的声明。
- 使用颜色来吸引眼球和传达信息。例如，你可以将新信息标记为蓝色，并将数学表达式的部分突出显示为红色。选择一种颜色方案并坚持使用它。
具体例子优于抽象概括性陈述
- 选择一个简单的例子，它是一般陈述的非寻常实例。最好构造这个例子，使得“附近”的误解是错误的。（例如，如果你想说明一个机制是过渡激励兼容的，确保在例子中它不是事后激励兼容的。）
你的听众最多只能记住七个不同的符号
- 他们的记忆是一种稀缺资源。不要浪费它。
所有幻灯片上的方程都是为观众阅读而设计的
- 停顿一下，给观众时间去消化它们。
- 你的观众已经知道你会做代数，因此长篇的推导不是表现能力的信号。
你会有一些不精确的说法和一些精确的说法，你的听众应该清楚地知道哪些是哪些
- “定理”、”命题”和”引理”仅表示精确、正确和被证明的陈述。如果你将其他陈述与这些陈述混在一起，你会损害听众对你的定理的信任。
提供高质量的少数内容，优于提供低质量的大量内容
- 通常每张幻灯片需要两分钟时间，不计算过渡时间。

复杂科学的信息论基础——最大熵原理²

建模和推断是多数科学领域的核心，尤其是对不断演进且复杂的系统。然而，我们所拥有的信息通常是不确定且不完善的，进而导致欠定推断问题（无穷多解）。以最大信息熵体系为代表的信息论为这类复杂问题提供了一种解决办法，并被广泛应用。

本文回顾了最大熵原理的发展历程、应用、在复杂系统中的拓展及最新进展。同时，本文也讨论了信息论推断的前沿工作：在有时变约束的复杂动态系统（如高度扰动的生态系统或快速变化的经济系统）的应用。

历史回顾

最早的信息论推断原理可以追溯到17世纪末Jacob Bernoulli的工作，他建立了在不确定条件下决策的数学基础，并被认为是概率论的开端。伯努利指出，如果我们没有关于某一特定结果的概率相关信息，我们必须等概率地处理所有可能结果。之后，辛普森、贝叶斯等人都独立地建立了更多数学上合理的推理工具，但最终是拉普拉斯凭借他对逆概率和逆推论概念的深刻理解，为不确定条件下的统计和概率/逻辑推论奠定了基础，最大熵原理和信息论就是在这项工资的基础上发展起来的。

到了两个世纪之后，香农关于通讯理论和信息熵的工作成为现代信息论的基础。Jaynes在此基础上概括了伯努利和拉普拉斯的不充分理由原理，确立了他关于最大熵原理的经典工作。

最大熵原理选择信息量最小的，与先验知识所施加的约束相兼容的概率分布。这样，对于先验知识没有提供的分布假设这一主观偏见就被消除了。最大熵形式的概率分布$p(n)$通过在约束条件下最大化香农信息熵$-\sum\limits_{n}p(n)log(p(n))$获得。

最大熵原理被大量的科学家应用，它的逻辑基础包括：

科学中，我们从先验知识出发，寻求拓展的知识
自然界中的知识几乎总是概率的，因此我们寻求的拓展知识总是可以通过概率分布的形式表达
先验知识总是可以表示为这一概率分布的约束
为了拓展已知，我们寻求的概率分布应该是最小偏差的，即分布不隐含或明确依赖于任何先验知识不包含的假设

为满足这四条逻辑基础，就应该最大化香农熵。

关于概率，有人支持频率学派，有人支持主观概率，而无论那种观点的概率都是基于一致信息的，因而都可以被统一到最大熵原理中，即拥有相同先验知识的不同分析者，无论其获取的知识有多么不完整，都会对推断分布得出相同的结论。

近期应用

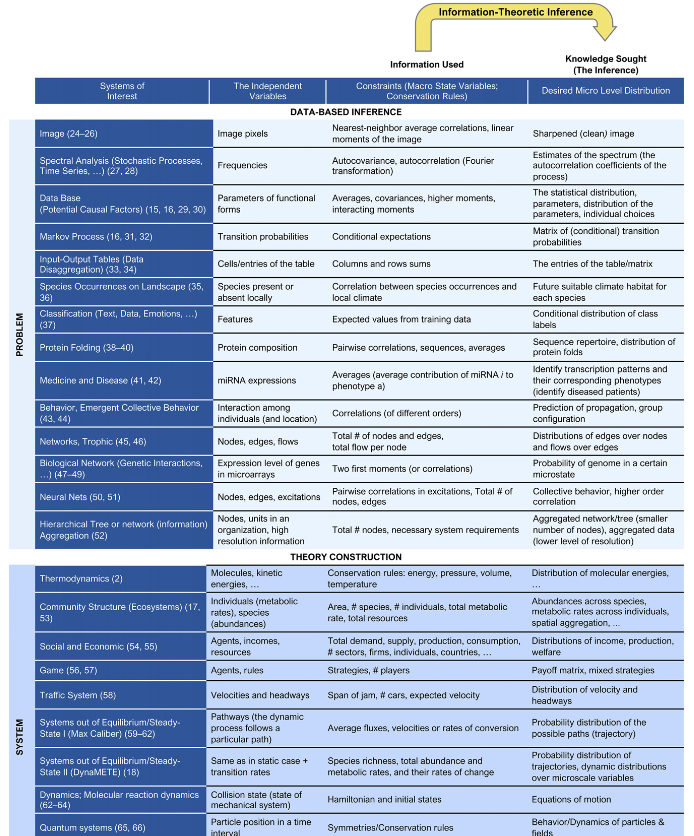
理论发展中的最大熵原理

与基于数据的推断不同，发展理论的最大熵原理是为了推断对各类系统中广泛现象全面统一的预测性理解构成的概率分布进行推断，而不是为了回答具体的问题。

许多复杂系统，如物理、生物、社会系统可以被近似表述为微观和宏观两个尺度。这类系统自下而上的模型与理论开始于选取系统微观组成部分中的主要驱动机制，之后基于微观驱动来预测宏观行为。这一方法的依赖于关于机制和参数的基本假设，然而这一假设却很少被验证。与这一思路相反的是，最大熵原理采用自上而下的方式推断概率分布，描述基于宏观约束形式体现的先验知识推理出的微观细节。如果没有最大熵原理，这一问题将会是欠定的，因为此为宏观约束不能独立决定微观变量高维分布的形状。

最大熵理论的批评与失败

选取状态变量和最佳概率分布过于武断，理论建构仅通过试错寻求合适的约束和目标函数反应自然界的准确预测模式

但事实上，即使是自下而上的模型也存在类似的问题，如任意选取函数形式、个体行为和用于描述微观互动的参数值。科学理论从来不是从逻辑中纯粹推导出来的，理论元素的选择通常部分地受到直觉和数据可获性影响。如果变量指定是正确的，约束被充分统计并捕获了描述系统行为所需的所有信息，该方法与香农熵目标函数提供了一种最简单的可证伪系统特征刻画。

最大熵理论没有明确的机制，不能获取因果洞察

当基于最大熵原理的理论成功时，无论决定状态变量的机制是什么，它都可以充分解释微观层面上的概率分布，为预测观察到的模式，不需要额外引入复杂性。因此，即使决定状态变量的实际机制是未知的，机制的作用是确定的。

最大熵原理和因果机制之间的联系源于一个重要观察：当用于建立最大熵原理的理论状态变量集不足以进行精准预测时，这种差异的性质可以为识别重要机制指明方向。

例如，热力学中，理想气体状态方程在状态变量的极端值下失败，推动了分子间范德华力的发现。

动力学系统中最大熵原理的拓展

如果状态变量在时间上发生变化，动态状态变量的瞬时值所施加的约束可能无法准确预测瞬时的微观尺度分布。

例如Harte等人把METE在偏离稳态时扩展为DynaMETE，其状态变量包含宏观变量的瞬时值、静态理论宏观变量的一阶导数、物种数量、个体数量和总体代谢率。它的一般结构适用于任何具有明确可区分的宏观状态和微观状态，其中微观变量的时间演变可以写成微观变量和宏观变量瞬间值的过度函数。

同时，最大熵理论为复杂系统的条件马尔可夫过程建模开辟了道路。我们通常使用时间序列数据推断稳态过度概率矩阵，但问题是当数据源自一个不断发展的复杂系统时，没有唯一的稳态过渡矩阵。因此我们考虑约束条件中可能存在模糊性和不确定性，可以得出一个近似的稳态过渡矩阵，它是基于数据的最可能过渡矩阵，以已知信息为条件，与所有观察到的复杂时间序列数据相一致。

沈凯玲丨我的那篇QJE

作者讲了自己当年回国工作，6年磨一剑的故事，很敬佩。在当下的经济大环境下，这样的故事无疑能带来一些慰藉。

图灵奖得主Geoffrey Hinton：我的五十年深度学习生涯与研究心法

类似的还有Hinton的故事，一个从物理转哲学又转心理学，又差点成了木匠的学生，阴差阳错学了当年冷门的人工智能专业。我之前听老师讲过Hinton创办了家公司，转手把自己和公司打包卖给Google这件事，我一直把它当做华尔街式的学术八卦，但没想到背后的故事是这样的。另外，没想到Hinton说他很烦数学，经常让学生给他讲数学，这是万万没料到的，原来还可以这样。

业界动态

BI+AI 有没有前途？

增强分析Augmented Analytics
- 自动数据洞察Automated Insight
  - Tableau：Explian Data
  - QickBI：波动原因分析
  - 远观数据：数据解释

电商领域A/B实验平台建设方法

确保样本独立性
- 版本翻转实验
  - 版本1使用策略1
  - 版本2使用策略2
  - ……不断翻转
  - 总体上分析两个测量的优劣
- 时间片轮转实验

技术技巧

Echart速查表

Echart Handbook

R：创建R包

教程：B站, CRAN-Writing R Extensions

创建R包

install.packages(c("devtools","roxygen2","testthat","knitr"))

devtools、usethis：构建R包的各种文件

roxygen2、knitr：生成R包所需的各类文档

testthat：测试R包

创建项目：File » New project » New Directory » package
1. 文件夹 ./R : R代码
2. 文件夹 ./man : 说明文档
3. 文件 DESCRIPTION：描述文件
4. 文件 NAMESPACE：声明导出、导入函数（一般不用主动编辑）
创建函数：参考./r中的hello.R
1. 建议将函数按功能或属性分开，便于维护
2. R包中的R文件只会在library时执行一次，然后保存所有生成对象，不会反复运行

添加说明文档

Description文件

  Package: package # 包的名称
  Type: Package # 项目类型
  Title: title # 标题（短描述）
  Version: 0.1.0 # （大版本.子版本.补丁版本）
  Authors@R: c(
      person('ZH','C',email = '...',role = c('aut','cre')),
      person('ZHH','C',email = '...',role = c('aut'))
      )
  # 需要有且只有1位维护者，role=c('cre')，且必须提供邮箱
  Maintainer: The package maintainer <yourself@somewhere.net>
  # 自动生成
  Description: despcription # 描述
  License: CC0
  # MIT允许人们使用和发布包的代码，唯一限制是许可证必须和代码一起发布
  # GPL-2任何包含本代码的包都必须使用GPL兼容的许可证发布
  # CC0作者放弃对代码和数据的所有权，任何人可以自由使用
  # 输入方式：usethis::use_mit_license()、usethis::use_cc0_license()
  Encoding: UTF-8
  LazyData: true
  Imports:  # 依赖包 usethis::use_package("packagename")
      ggplot2
  RoxygenNote: 7.2.2

文档
1. 函数文档
  1. 书写注释
    1. 标题
    2. 描述
    3. @param 参数名描述
    4. @return 返回值描述
    5. @examples, @references
  2. 创建帮助文档
    1. 1 devtools::document()
    2. ./man/function.Rd
2. 包文档等非函数文档
  1. 1 devtools::document
3. NAMESPACE
  1. 绕过NAMESPACE
    1. 直接在需要的函数中写library
  2. 不绕过NAMESPACE
    1. export函数
      1. 某些函数不公开给使用者
    2. import函数
      1. 调用别人函数

上传

github

安装创建的R包

devtools::install_github("username/repositoryname")

娱乐

量子金融：一种新的经济学方法论丨量子世界地图

很有意思的想法！但我现在还不想学…如果以后需要参考再回来看。

量子现金和“真实”货币不存在，及货币二象性
房地产经纪人不确定性原则
薛定谔银行账户
Black Scholes模型
相对论效应和财务质量
现金/能量守恒定律和费曼现金流图
虚拟经济粒子和暴胀宇宙

Donoho, D. (2017). 50 Years of Data Science. Journal of Computational and Graphical Statistics, 26(4), 745–766. https://doi.org/10.1080/10618600.2017.1384734 ↩
Golan, A., & Harte, J. (2022). Information theory: A foundation for complexity science. Proceedings of the National Academy of Sciences, 119(33), e2119089119. https://doi.org/10.1073/pnas.2119089119 ↩

【阅】本周阅读摘选2023-03-20 → 2023-03-26