学术相关
社会韧性续篇
突然发现之前那篇完成度不是特别高的测量社会韧性文章1有续篇了!这次感觉比上一次有了一定的推进,但是距离作者设立的宏大的社会韧性的目标还是有较大的距离,这两个研究应该还是阶段性的成果。
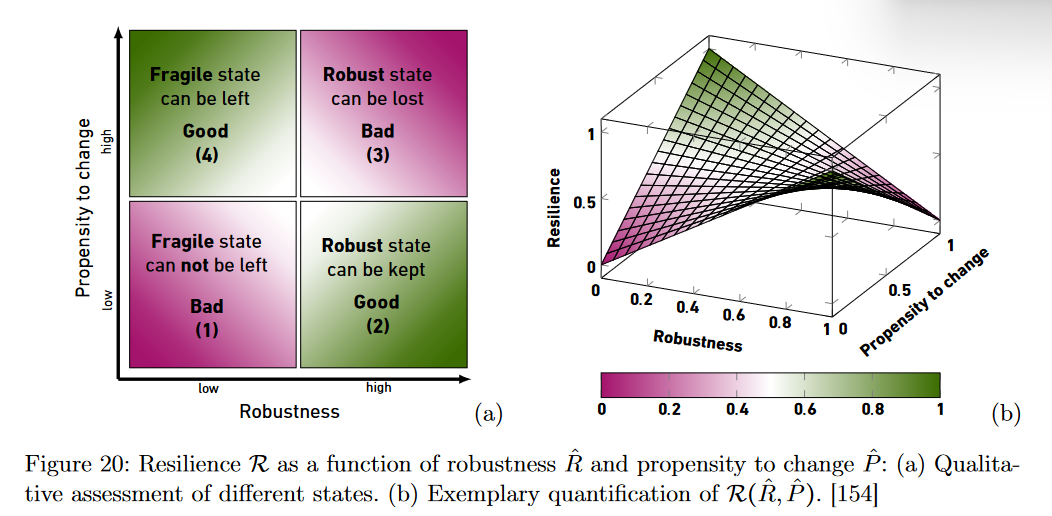
回顾:社会韧性包含鲁棒性和适应性
令社会韧性为$R$,鲁棒性为$\hat{R}$,适应性(柔性、灵活性)为$\hat{P}$
$R(\hat{R},\hat{P})=\hat{R}(1-\hat{P})+\hat{P}(1-\hat{R})$
Adapting to Disruptions: Flexibility as a Pillar of Supply Chain Resilience 2(柔性为主)
这篇文章比较遗憾的是它主要讨论了供应链柔性(上游偏好/替代路径),但为了简化模型,对于鲁棒性(安全库存等)没有深入探讨和仿真。
为提高供应链韧性,减少供应链断裂的风险,人们通常使用两种方案:一种是创建冗余的分销链路;另一种是在已建成的供应链中寻求替代品。作者对美国止疼片分销系统进行了实证分析,基于数据驱动的模型重建了基于400亿条分销路径数据,并对增加替代柔性的政策进行独立审查。最终,作者指出他们的方法能够使管理者量化增加柔性与增加供应链复杂性之间的权衡关系。
作者使用的数据集是ARCOS,它列出了2006~2014年美国止痛片分销系统的所有药品运输数据并经常受到短缺影响。
上游偏好与柔性
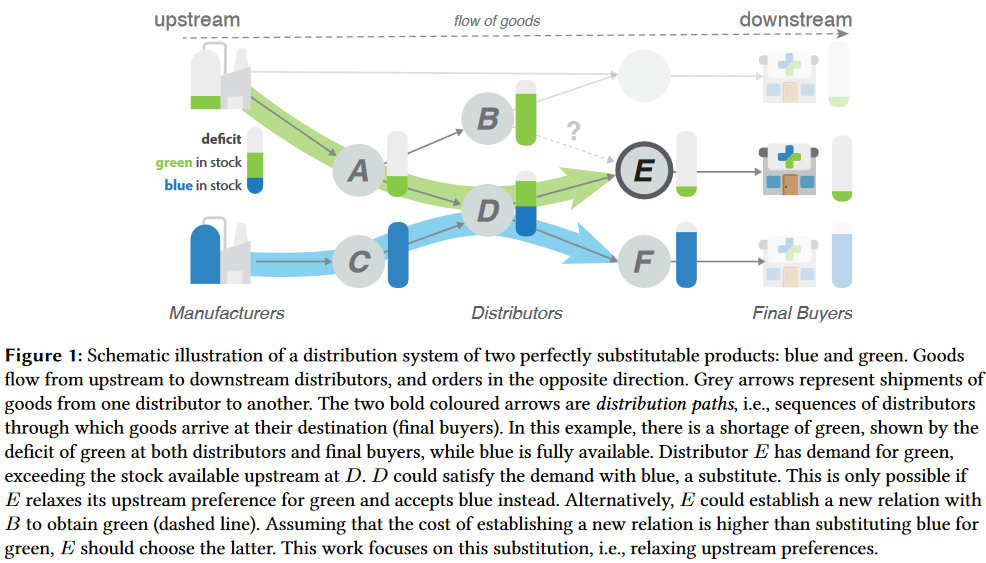
若分销商E相较于C(blue)严格偏好A(green),用概率的语言表示为$Pr(E\to D\to A)=1\ and\ Pr(E\to D\to C)=0$;同时,若分销商E对C(blue)和A(green)没有任何的偏好,它接受任何上游D分配的物资,则$Pr(E\to D\to A)=Pr(D\to A)=0.5\ and\ Pr(E\to D\to C)=Pr(D\to C)=0.5$,柔性$\phi_E$可表示为分销商放松对上游偏好的倾向,即$\begin{aligned}Pr(E\to D\to A|\phi_E)&:=\phi_E\ Pr(E\to D\to A)+(1-\phi_E)Pr(D\to A)\\Pr(E\to D\to C|\phi_E)&:=\phi_E\ Pr(E\to D\to C)+(1-\phi_E)Pr(D\to C)\end{aligned}$。
数据建模
- 基本假设
作者设置的可替代性基于FDA定义的“药理学等效”,同时作者基于前人研究的药物必需品价格弹性很低的原因排除了价格效应。
在分销系统方面,作者假设了FIFO先进先出法。
作者为独立的药物包裹重构了400亿条分销路径,令重构路径$P:={p_1,…,p_S}$,其中每个元素为单一药物包裹的单一路径。每条路径被表示为元组$p_s=(M\to k\to j\to …\to i)$,其中$M$为制造商,$k、j、i$为分销商,其中$i$为将药物送达最终消费者手中的最后一个分销商。
- 分销系统高阶马尔科夫链模型
作者发现重构的物流路径长度在1~4之间,其中大多数长度为2(1个制造商和2个分销商)。基于这一观察,作者采用了高阶马尔科夫链来建模包含2步上游偏好的模型。
考虑2步分销路径$p_s(k\to j\to i)$通常为完整路径或长路径的子路径,作者定义$\tilde{A}_{kji}$为$p_s$在数据中出现的总数,将其作为完整路径和子路径的情况加总。
同时,作者假设了市场完美出清。因此,$i\to j\to k$的需求订单$A_{ijk}=\tilde{A}_{kji}$。
作者基于高阶马尔科夫链构建3维张量$T^{2-step}$。$T_{ijk}^{2-step}=\frac{A_{ijk}}{\sum\limits_{j’k’}A_{ij’k’}}$,其中求和了所有的子路径$(j’\to k’)$,即$T^{2-step}$的每个元素表示订单沿路径$(i\to j\to k)$的转移概率。
- 完全放松上游偏好
有时候分销商会放松它们的上游偏好,作者引入2维矩阵$S$来表示,给定元素$S_{ij}$捕获了$i$向$j$下订单的概率。其中,$S_{ij}=\sum\limits_k T_{ijk}^{2-step}$。基于此,作者构建了新的张量$T^{1-step}$捕获了上游1步以内的偏好,同时对长度为2的路径进行建模,$T_{ijk}^{1-step}=\frac{S_{jk}}{\sum\limits_{k’}S_{jk’}}\cdot\Theta(\sum\limits_{k’}A_{ijk’})$,其中$\Theta$在$i\to j$路径上至少有一个订单时为1,否则为0,而右侧只有$jk$是因为假设$i$完全放松了上游偏好,使其订单完全与中间商$j$对齐,此时$i$对$k$的订单比例只取决于$j$对$k$的订单比例。
- 柔性
上游偏好的放松程度取决于分销商的柔性水平$\phi_i$,因此作者结合了$T_{ijk}^{1-step}$和$T_{ijk}^{2-step}$,即$T(\phi_i)_{ijk}=\phi_iT_{ijk}^{1-step}+(1-\phi_i)T_{ijk}^{2-step}$,其中$\phi_i$为两种极端情况的插值。
- 估计实证柔性
作者使用极大似然估计给定时间域$h$的系统柔性。特别地,作者使用在$[t-b,t]$期间的运输张量$B(b,\phi)$估计每个分销商的上游偏好,其中$b$为偏好估计周期,$\phi$是$n$维向量,$\phi_i$为分销商$i$的柔性。
作者令$B(b,\phi)$为订单运输张量$T(\phi, b)$,其原理是假设每个分销商的预期出货量等同于预期订单。$B_{ijk}(b,\phi_k):=\frac{T_{kji}(b,\phi_k)\cdot v_k}{\sum\limits_{k’j’}T_{k’j’i}(b,\phi_{k’})\cdot v_{k’}}$,其中$T_{ijk}(b,\phi_k)$为在$[t-b,t]$期间的$T(\phi_i)_{ijk}$,$v_k=\sum\limits_{lm}A_{klm}$是$k$下订单的总量。
之后,观察$[t,t+h]$期间的运输张量$\tilde{A}(h)$,元素$\tilde{A}_{ijk}(h)$捕获了在$[t,t+h]$期间$i\to j\to k$的运输量。
因此,似然函数$\mathcal{L}(\phi)=[\prod\limits_{i,j,k}B_{ijk}(b,\phi_k)]^{\tilde{A}_{ijk}(h)}\propto\ log\mathcal{L}(\phi)=\sum\limits_{i,j,k}\tilde{A}_{ijk}(h)log B_{ijk}(b, \phi_k)$
$\hat{\phi}=arg\ \mathop{max}\limits_{\phi}\ log\mathcal{L}(\phi)$
在本研究中,作者将$b$和$h$都设定为$1\ year$。
- 建模附加上游偏好的分销动力学
为研究分销动力学如何依据柔性水平变动,作者将上游偏好拓展进了ARIO自适应区域投入产出模型。在ARIO中,分销商通过下订单来满足需求并维持安全库存$s^T$。
$o_{(i|j)}(t)=d_{(i|j)}(t-1)+\frac{1}{\tau}[S_{(i|j)}^T-s_{i|j}(t)]$,其中$o_{(i|j)}$为$i$向$j$下单量,$d_{(i|j)}$是$i$对从$j$处商品的需求量,它具体包含终端用户订单向量$c$和其他分销商订单矩阵$o$两类。参数$\tau$衡量了分销商$i$希望恢复库存的速度,为简化模型,作者假定$\tau=5\ days$同质且不变。$s_{(i|j)}$表示$i$用于存储自$j$处接收的货物子库存,子库存依据运入、运出更新$s_{(i|j)}(t)=s_{(i|j)}(t-1)+W_{(i|j)}^{in}(t-1)-[W_{(i|j)}^{out}(t-1)+w_{(i|j)(t-1)}]$,其中运出总量包含从终端消费者消费$w_{(i|j)}$和其他分销商消费$W_{(i|j)}^{out}$。
因此,分销商带有上游偏好的下单量表示为$O_{ijk}(t)=o_{(i|j)}(t)T_{ijk}(\phi)$。
最后,作者补充假设了分销商希望尽可能地满足需求,使其发货量总是等同于其所面临的订单量和库存水平之间的最大值。
- 利用真实数据初始化模型
作者假定了分销商在观察年$y$完美地满足了需求,则常数日常需求为$c_i=\frac{w_i(y)}{365}$,其中$w_i(y)$表示$i$在$y$年运向最终消费者的总额。
给定路径$j\to i$的供给份额根据数据初始化为$c_{(i|j)}=c_i\frac{W_{(i|j)}^{in}(y)}{\sum\limits_{j’}W_{(i|j’)}^{in}(y)}$。
在完全满足需求的假设下,目标安全库存是在年底观察到的实证缓冲存量$s_i^T=W_i^{in}(y)-[W_i^{out}(y)-w_i(y)]$。则根据份额分配的目标安全子库存为$s_{(i|j)}^T=s_i^T\frac{W_{(i|j)}^{in}(y)}{\sum\limits_{j’}W_{(i|j’)}^{in}(y)}$。
在模拟的开始时刻,所有的分销商的库存水平都被设定为目标安全库存。
- 模拟供应冲击
假定一个减少$\sigma$%总供给的外部冲击,$s_i(t=t^*)=(1-\sigma)s_i(t-1)\ \forall i\in{m_1,…,m_n}$,其中$s_i$表示了制造商库存水平,$t^*$为冲击时刻。
- 衡量供给赤字
供给赤字$\delta(t)=\frac{\sum\limits_{t’=0}^t\sum\limits_iw_i(t’)-c_i}{t\times\sum\limits_ic_i}$,其中$i$为所有运向终端消费者的分销商,即表示为累计未满足需求的终端消费者的百分比。
作者补充假设了订单会在第二个工作日抵达。
- 衡量替代路径的使用
作者通过百分比的方式量化柔性带来效应$\Gamma(t)=\frac{\sum\limits_{ij}|W_{(i|j)}(\phi,t)-W_{(i|j)}(\phi=0,t)|}{\sum\limits_{ij}|W_{(i|j)}(\phi=1,t)-W_{(i|j)}(\phi=0,t)|}$。
柔性缓解短缺模拟
分销系统压力测试
作者使用分销系统压力测试模拟的方式来探索经验分销系统对供应链的反应。具体地,作者数据驱动地模拟了基于需求订货并分配商品的供应商智能体模型。
为模拟供货突然中断的情形,作者基于数据设定了在中断时间$t=0$的时候上游分销商存货量为最大存货量的70%。根据这些设定作者模拟了Oxy分销系统终端消费者在不同时间的供应短缺情况,如果没有柔性,在40天后终端消费者出现6%(三百万剂)的短缺。
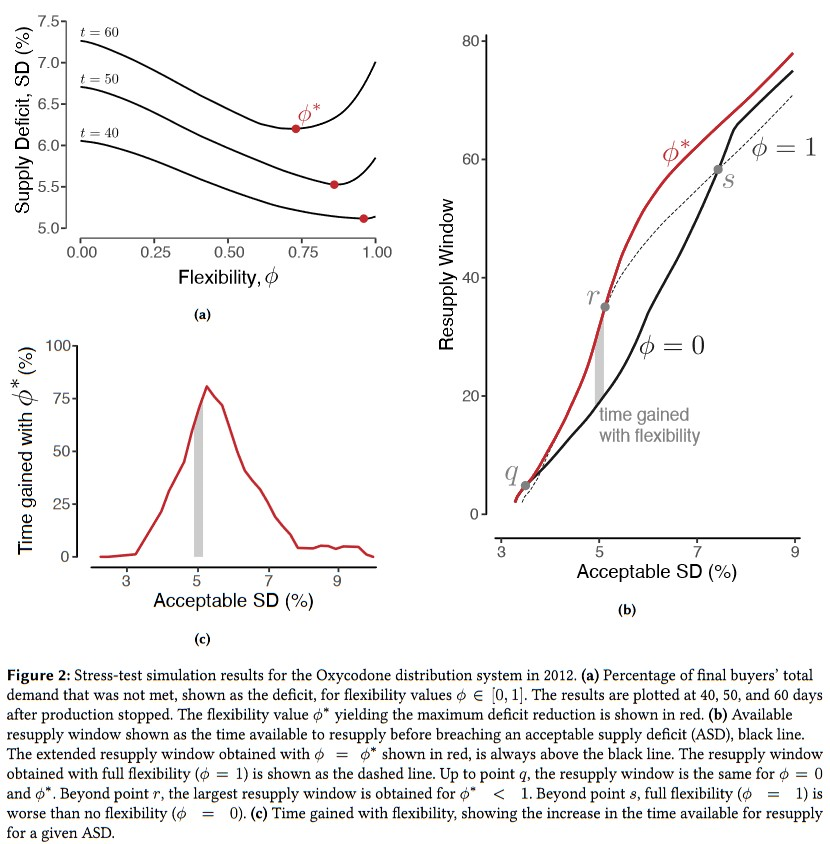
为分析柔性程度如何影响终端消费者供应赤字情况,作者首先假定了所有分销商的柔性$\phi$均相同,在图$2a$中可以看到$t=40$时,柔性从0到1可以减缓接近1%的短缺。同时,结果也表明最佳柔性$\phi^{\ast}$可能小于1。
作者并未对此作详细说明,我猜测可能过大的柔性会导致商品过快地流动,延长供应环节,进而增加了途中时间开销。
但由于作者没有给出具体的数据和模型细节,我无法确认。(从后面看应该是这个原因)
可接受供应赤字模拟
某些物品必须保证一个最低供应量,在Oxy的例子中,可接受供应赤字ASD为不危及病人安危的前提下的最大短缺水平。
因此,我们就可以对给定的ASD计算恢复供应的窗口期长度。如图$2b$所示,较小的ASDs柔性的益处是有限的,但对较大的ASDs柔性可能延长较长的窗口期。图$c$显示了百分比收益,当ASD在5%左右处最佳柔性能带来最大的收益。
柔性的实证证据
同比柔性$\hat{\phi_i}(y)$捕获了分销商$i$相对于$y-1$年,在$y$年放松上游偏好的程度。给定上一年的上游偏好水平和当年的观测分配路径,作者采用了极大似然法推断$\hat{\phi}_i(y)$。
实证数据表明,每一年分销商都有一定的柔性水平,平均而言数据集中的分销商柔性水平通常较低,但高柔性会周期性出现。
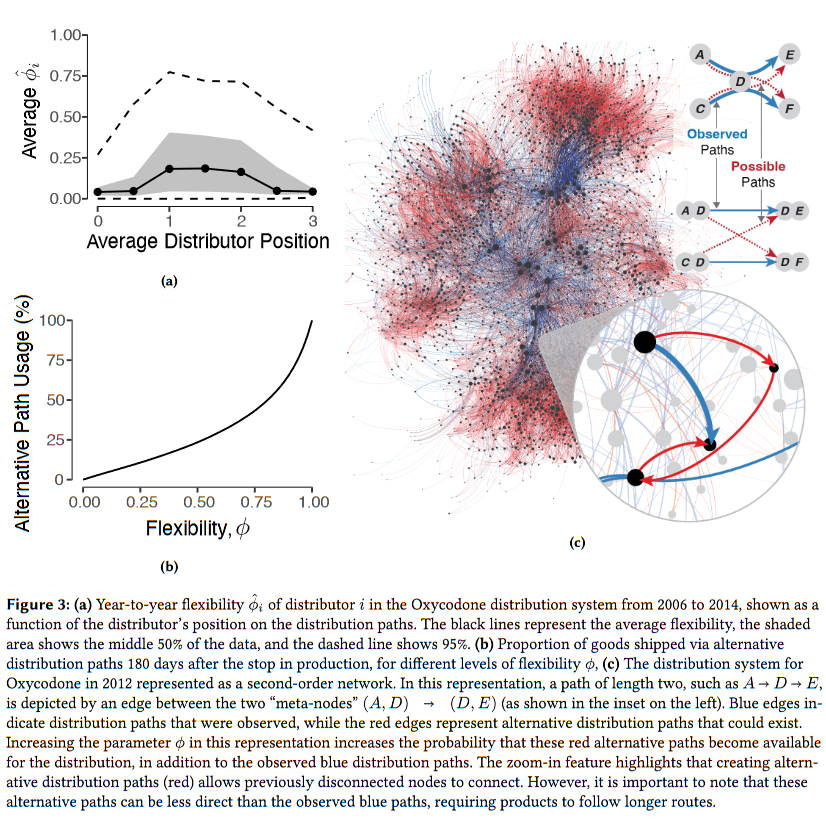
图$3a$为2006~2014年Oxy分销系统分销商$i$的同比柔性$\hat{\phi}_i$,黑色实线为平均柔性,阴影区域为中间50%的数值,虚线为95%的区间。结果表明在供应链中游的分销商通常具有较高的柔性。
供给赤字减少与柔性开销的权衡
如图$3b$所示,柔性为分销商带来了额外的可选择分销路径。图$3c$具体展示了替代分销路径引入的位置,蓝色边展示了实际分销路径,而红色边展示了在$\phi=1$时产生的替代路径。同时,图$3c$展示了大多数柔性带来的替代分销路径位于分销系统的边缘。
柔性成本
增加分销路径通常会带来额外的开销,同时也可能减缓分销速度,因为一些分销路径(如zoom-in区域)并不直接。
- 减速因子
为比较柔性和严格上游偏好之间的分销速度差异,作者引入了减速因子概念。令$M$为行随机转移矩阵,它描述了网络中的一个随机游走。前人研究已经证明,节点访问概率从任何初始条件开始,收敛到平稳分布所需的时间$t\approx \frac{1}{log|\lambda_2[M]|}$,其中$\lambda_2[M]$为$M$的第二大特征根。
现考虑$B_{ijk}(b,\phi_k):=\frac{T_{kji}(b,\phi_k)\cdot v_k}{\sum\limits_{k’j’}T_{k’j’i}(b,\phi_{k’})\cdot v_{k’}}$,令向量$v=\mathbb{1}$,元素$B_{ijk}(b, \phi)$是关于柔性$\phi$的货物沿$i\to j\to k$运输的概率函数。将表示两步转移的$B(b,\phi)n\times n\times n$张量映射到等价的$n^2\times n^2$二阶转移矩阵$\tilde{B}_{(i,j)(m,k)}(b,\phi)=\left\{\begin{array}{rcl}B_{ijk}(b,\phi)\ & iff\ m=j,\\ 0\ &otherwise.\end{array}\right.$,如果$i\to j$不存在则二阶节点也不存在。
令$\Omega$为最终分销商的集合,因此结合最终分销商$w\in\Omega$和最终节点$\dagger$,终端的分销路径可以表示为$\tilde{B}_{(w,\dagger)(\dagger)>0\ iff\ w\in\Omega}$,最终设置$\tilde{B}(\dagger)(\dagger)(b,\phi)=1\forall\phi$确保马尔科夫链是吸收的,并有独特的平稳分布$(0,…,0,1)$,其中最后一个元素对应最终节点$\dagger$,使最终游走收敛于$(\dagger)$。
最终,作者将减速因子$\sigma(\phi)$定义为与$\phi=\mathbb{0}$相比访问概率收敛到其平稳分布所需的额外步骤数:$\sigma(\phi):=\frac{log|\lambda_2[\tilde{B}(b,\mathbb{0})]|}{log|\lambda_2[\tilde{B}(b,\phi)]|}$。
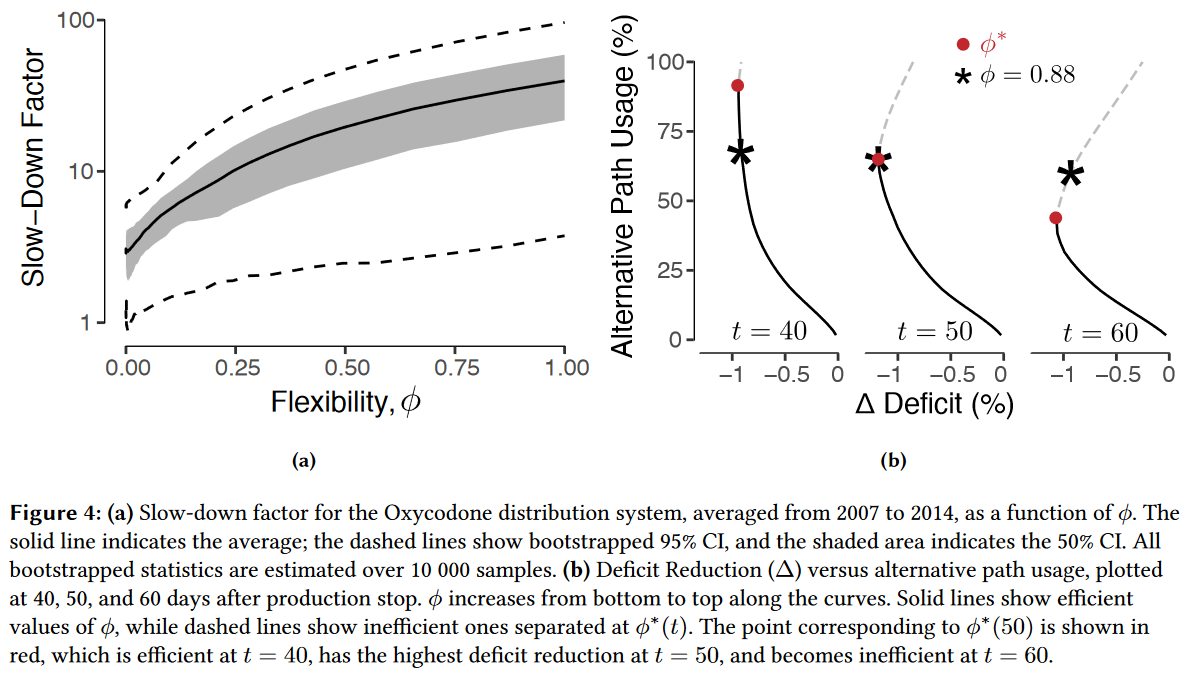
图$4a$展示了柔性水平与减速因子的关系,柔性越大,商品的分销路径越长,进而使成本上升。
- 柔性回报递减
图$4b$展示了供给赤字的减少和替代路径的运用关系,结果表明在曲线上部存在低效集(虚线)。
总的来说,作者提供了一种可以探讨供应链柔性的方式,并表明适当的柔性可以缓解短缺,但过大的柔性也会带来额外成本,需要仔细权衡。
Detecting and Optimising Team Interactions in Software Development3(阶段性研究)
这篇文章应该还是有较多不够成熟的地方,我认为从作者意图构建社会韧性测量之一大图景出发,这篇文章应该是测量敏捷团队韧性这一主题下的偏工具性的阶段研究。
本研究基于软件开发人员在开发平台上的日常工作记录,通过数据驱动方法检测开发团队的功能性互动结构。作者提出的方法考虑了团队成员不同的活跃水平,并利用一种区块约束配置的模型计算不同工作角色的开发人员之间的互动表现。作者还通过与5名团队成员进行半结构化访谈的方式验证了检测到的功能性互动结构的正确性。此外,作者估计了团队中的知识扩散水平,并提出可优化区域来帮助团队实现实时团队互动结构管理。
当下的迅捷软件开发团队(如高度依赖自组织且组织灵活的开源团队)通常具有高水平的适应性、持续演化和对需求灵活反应的能力,因此实时地了解其互动结构存在难度。如果缺乏对互动结构的管理,团队有可能出现产出低效、低质,缺乏有效信息互动,甚至关键成员脱离等问题。
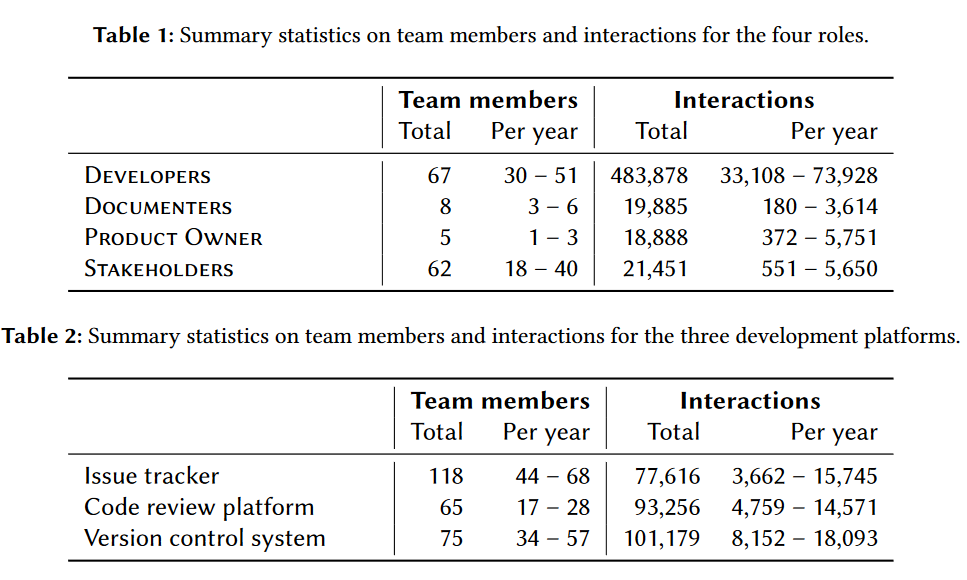
作者基于德国IT安全公司Genua GmBH产品团队在3个沟通平台上的数据进行了实证研究。Genua产品团队中存在4种角色:开发者$D$、用户手册编辑、产品负责人、编外人员$S$(杂活)。
该产品团队使用3种平台跟踪工作:issue tracker(REDMINE) - 特性请求&bug修复;code review platform(AEGIS) - 代码审查;Version control system(Git2net)- 版本控制。
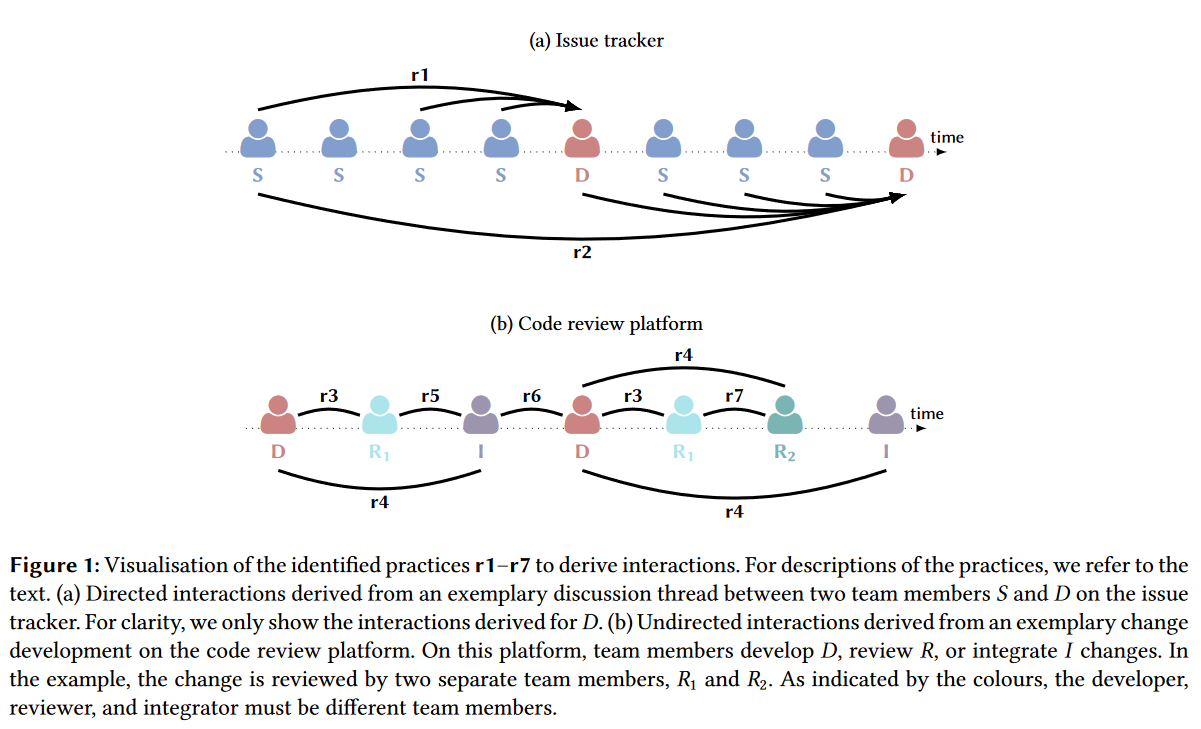
互动结构检测
互动计数法
一个最朴素的方法是简单统计每个角色对的成员互动频次,并进行简单分析。
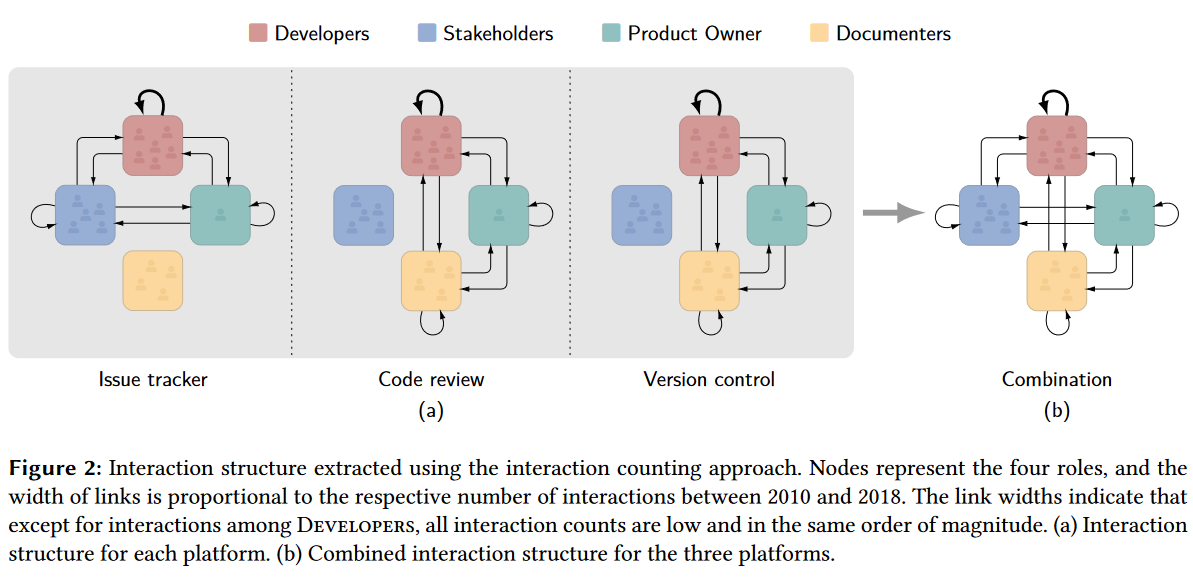
结果表明,除了开发人员之间的互动外,所有其他角色之间的互动都近似地低。
然而,互动计数法法忽略了每个角色发起/收到互动的可能。
假设一个拥有2名编外人员、3名开发人员和1名产品负责人的合成样本,编外人员之间有中等强度的互动活跃性,开发人员之间有高强度的互动活跃性,负责人需要协调两组人,他与开发人员之间互动了50次,与编外人员互动了10次。但这是否意味着产品负责者更偏好于开发人员互动呢?互动计数法认为是这样的,但作者不同意,因为从比例上产品负责人只参与了开发人员互动的1.9%(30/1550),却参与了编外人员互动的33.3%(10/30)。
区块模型方法
作者使用区块约束设置模型BCCM将团队成员的角色设定为区块,实现控制计算中角色的活跃度。作者使用R包GHYPERNET,在BCCM中引入了$w_{r_1r_2}$来根据角色在互动网络中的入度和出度衡量其互动倾向$w_{r_1r_2} := -log(1-\frac{A_{r_1r_2}}{\Xi_{r_1r_2}})$,其中$r_1$、$r_2$为两个角色,$A_{r_1r_2}$为对应角色团队成员的互动数量,$\Xi_{r_1r_2}$为$r_1$与$r_2$之间的最大可能互动数量,使之作为归一化项。
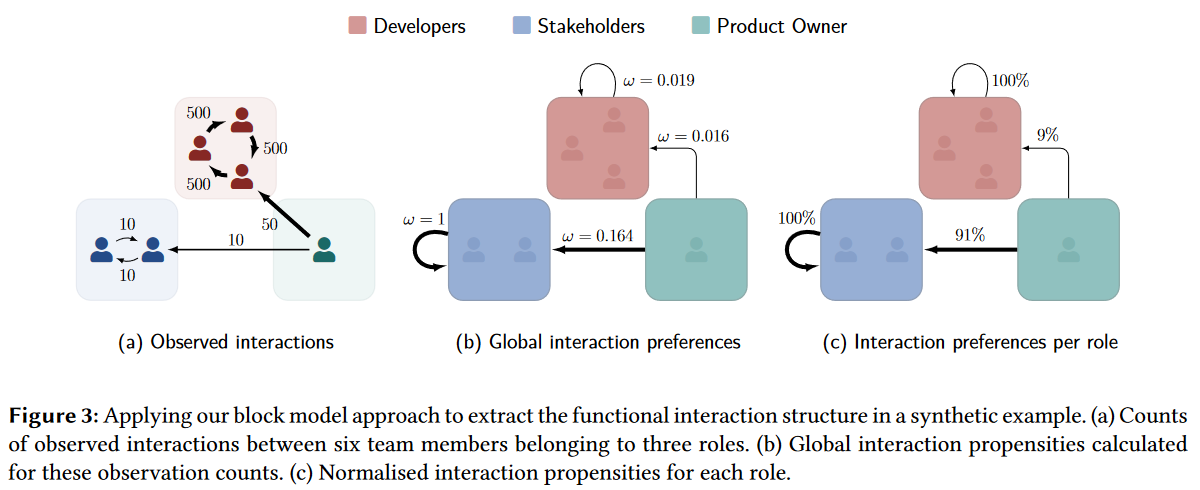
图$3a$展示了互动计数的结果,图$3b$展示了所有角色对的$w$值。结果与互动计数法相反,产品负责人与编外人员互动的倾向是与开发人员互动倾向的10倍。
但从问题角度上看,似乎没有说明什么实际价值
Genua公司互动结构检测
由于团队包含4个角色,所以作者将区分积极/消极偏好的阈值设定为25%。消极偏好是对积极偏好的补充,它们通常很不活跃。
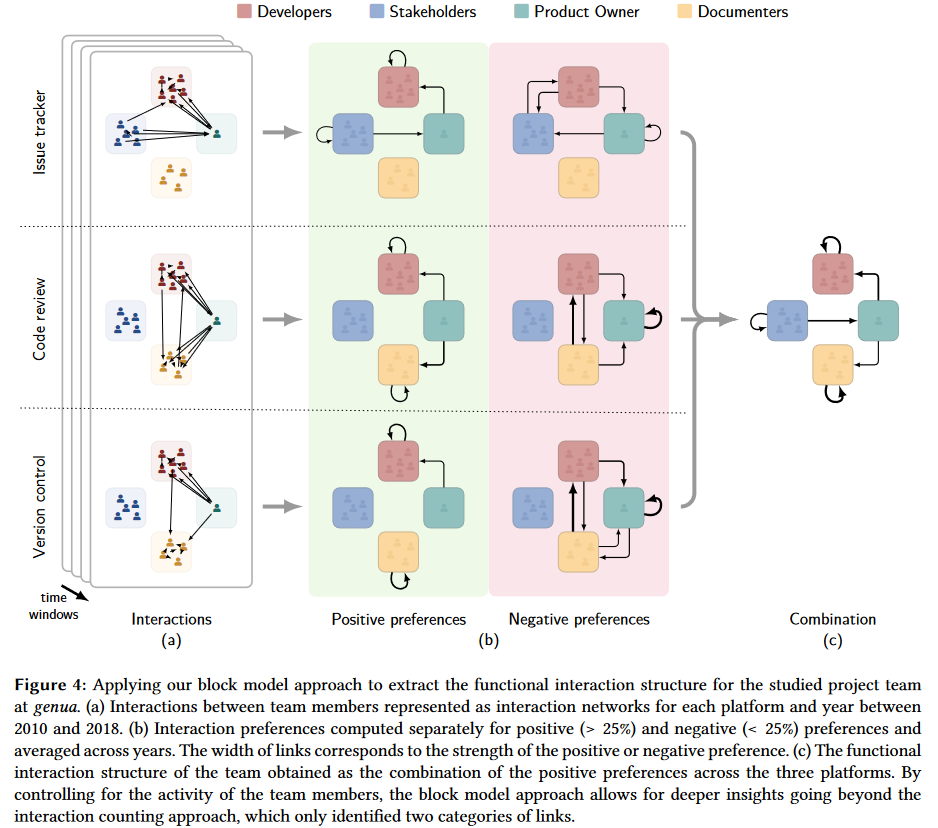
为验证检测到的互动结构,并通过功能信息丰富这一结构形成组织结构图,作者对2名开发人员,2名编外人员和1名前产品负责人进行了半结构化访谈。
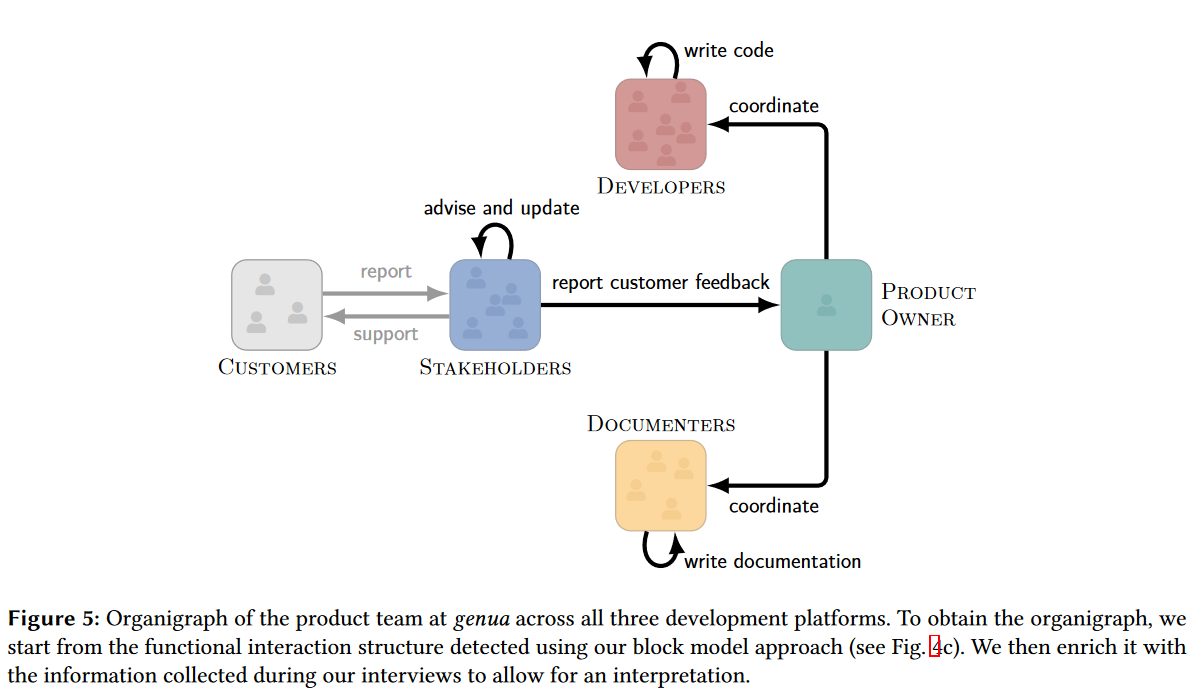
互动结构优化
之前的环节将特定的角色转换为了交互网络中的单一节点,这里暗含着所有员工都被认为是同质的假设。这一假设过强以至几乎不会出现,访谈中编外人员和开发者的知识、技能都体现出明显的异质性。
然而,敏捷开发的方式却需要致力于提升角色内的知识扩散水平,达到“Everyone can do everything”,进而降低特定成员离开团队的风险。
作者使用潜在性Potentiality(Pot)概念,利用熵法量化成员在整个团队中的互动程度,而非几个合作者之间的互动。
$Pot:=\frac{H^{observed}}{H^{max}}\in[0,1]$,这里$H^{observed}$是观测到的互动分布的熵,$H^{max}$指所有团队成员与每个人以同等频率互动所达到的最大熵。$Pot$越接近1意味着更多的成员与整个团队进行交互。
当我们给定一个互动结构(BCCM),使用R包GHYPERNET进行抽样获取可能的互动网络分布,之后计算交互网络的潜在性。这样就可以得到不同互动结构下的团队知识扩散水平。
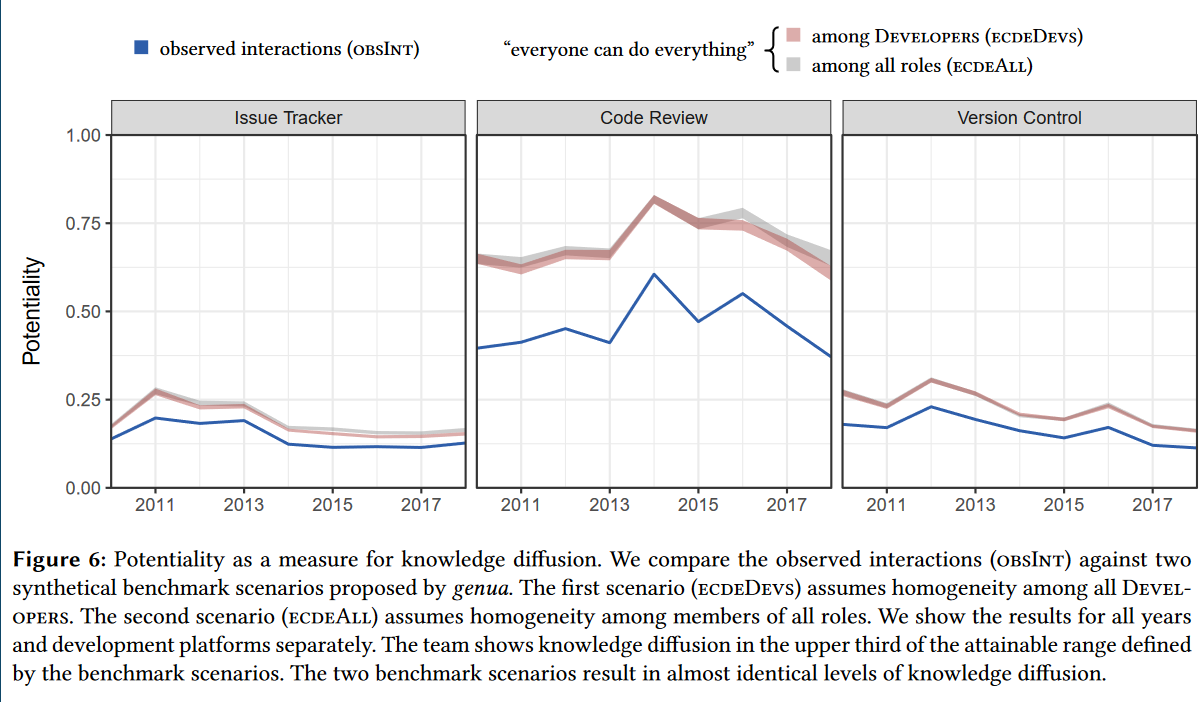
作者发现在所有平台的所有年份里,$Pot(\tiny{ECDE}\normalsize{A}\tiny{LL}\normalsize)>Pot(\tiny{ECDE}\normalsize{D}\tiny{EVS}\normalsize)>Pot(\tiny{OBS}\normalsize{I}\tiny{NT}\normalsize)$。此外,$\tiny{ECDE}\normalsize{D}\tiny{EVS}$与$\tiny{ECDE}\normalsize{A}\tiny{LL}\normalsize$的差距通常较小,所以几乎所有知识扩散带来的提升都可以归结为开发者的”Everyone can do everything”。在实验中,该团队的最佳知识扩散水平应该是$\tiny{ECDE}\normalsize{A}\tiny{LL}\normalsize$达到70%左右,为团队优化提供了建议。
有效性的威胁
这一研究存在较多的局限性。
- 数据获取仅局限于三个平台的互动记录,不包含互动内容和其他互动方式
- 平台记录的是行为而非互动,作者虽然做了一些处理但应该还是存在一定问题
- 作者使用团队成员的观点验证模型结果,但可以存在访谈遗漏的关系
- 由于缺乏交互文本,作者对知识扩散的讨论不足
- 假设成员同质性,未讨论异质性
- 存在外部效度问题
作者表明,基于熵的测量,可以量化整个团队的互动分布进而表示知识岛的韧性,接着使用程度同构性和聚类协数可以测量一个核心开发者离开对团队的影响。
此外,该方法也有助于检测小群体的出现,识别知识扩散水平较低的团队角色,降低风险。
最后,这一方法为互动结构优化提出了一些指标性建议。
技术技巧
Python库:ABM框架Mesa
Mesa是一个模块化的Python ABM框架,它致力于成为Python界的NetLogo。
demo: 谢林隔离模型Schelling Segregation Model
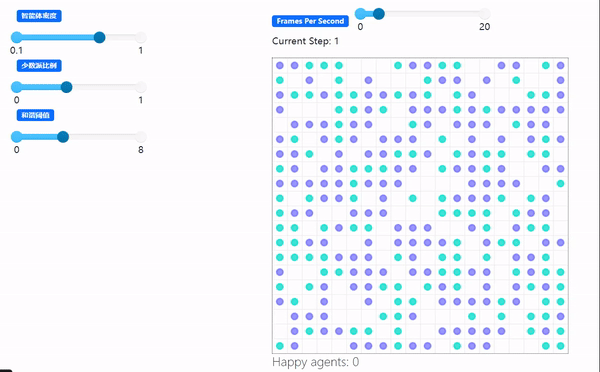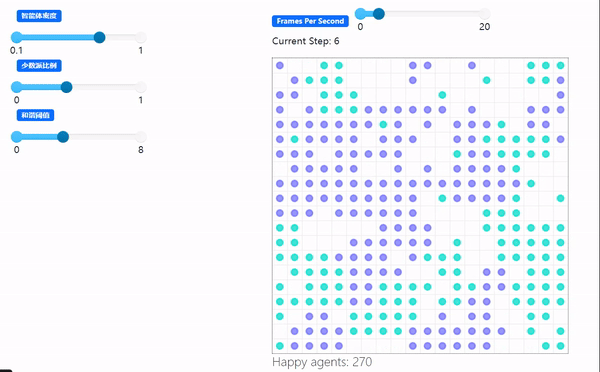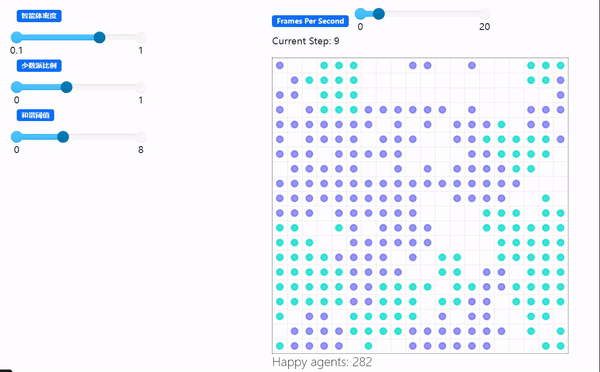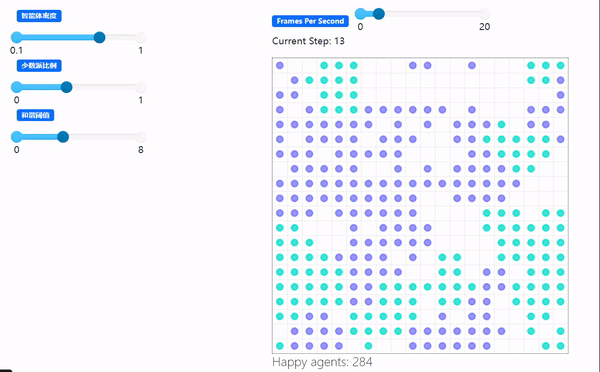
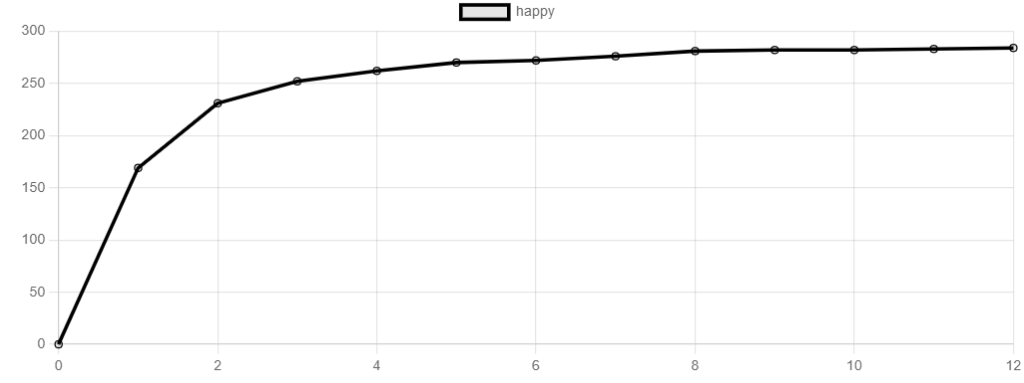
python: 微信公众号爬虫
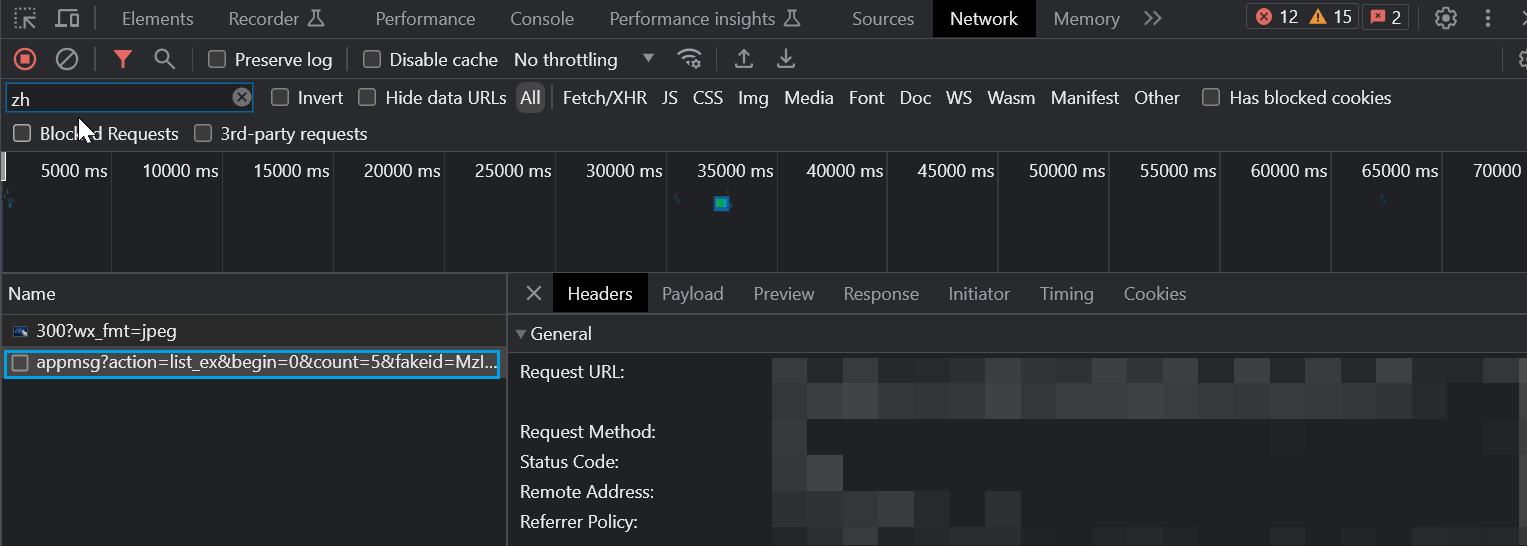
- 获取真实URL
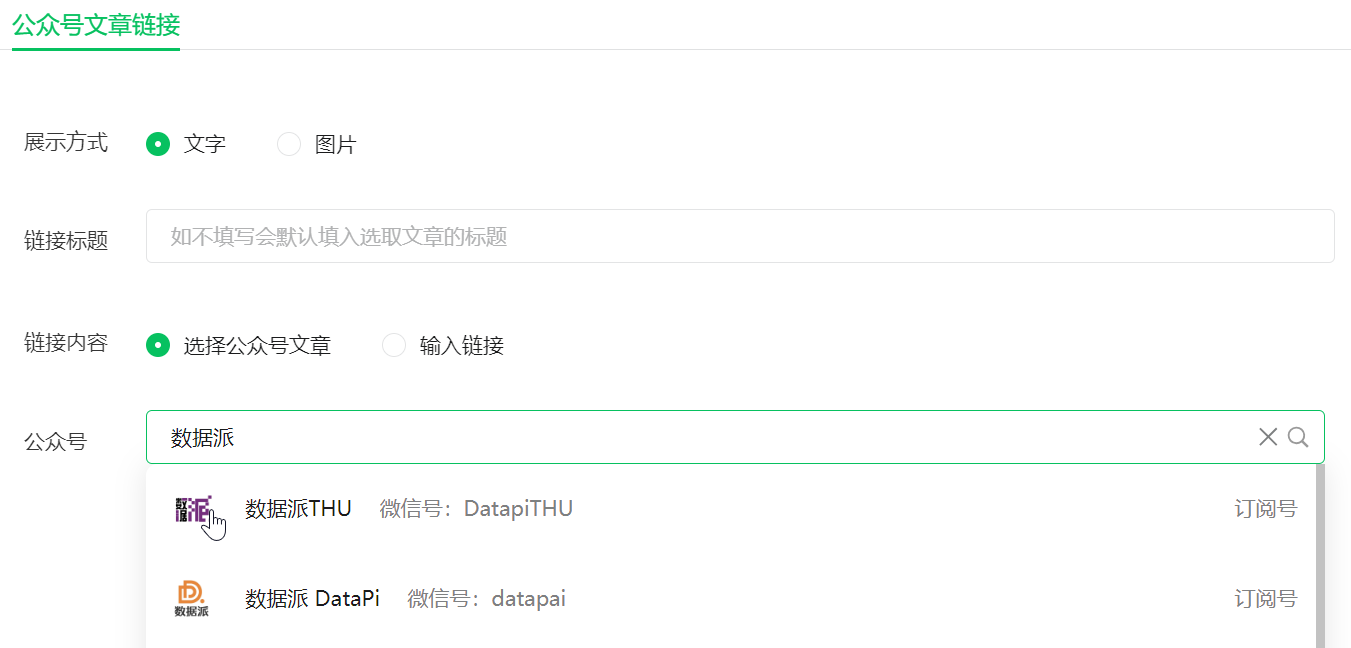
微信公众平台→新的创作:图文消息→超链接→公众号:选择其他公众号→检索欲爬取的公众号(不选中)→检查:Network→选中公众号→appmsg项目Request URL
|
新的创作:图文消息  |
超链接 
公众号:选择其他公众号  |
- 设置Cookie和User-Agent
- URL解析
- 基础部分:https://mp.weixin.qq.com/cgi-bin/appmsg
- 动态网站:?action=list_ex
- 迭代部分:&begin=0 (0,5,10,15,……)
- 其他:……
R: Nature子刊相关性网络图复现
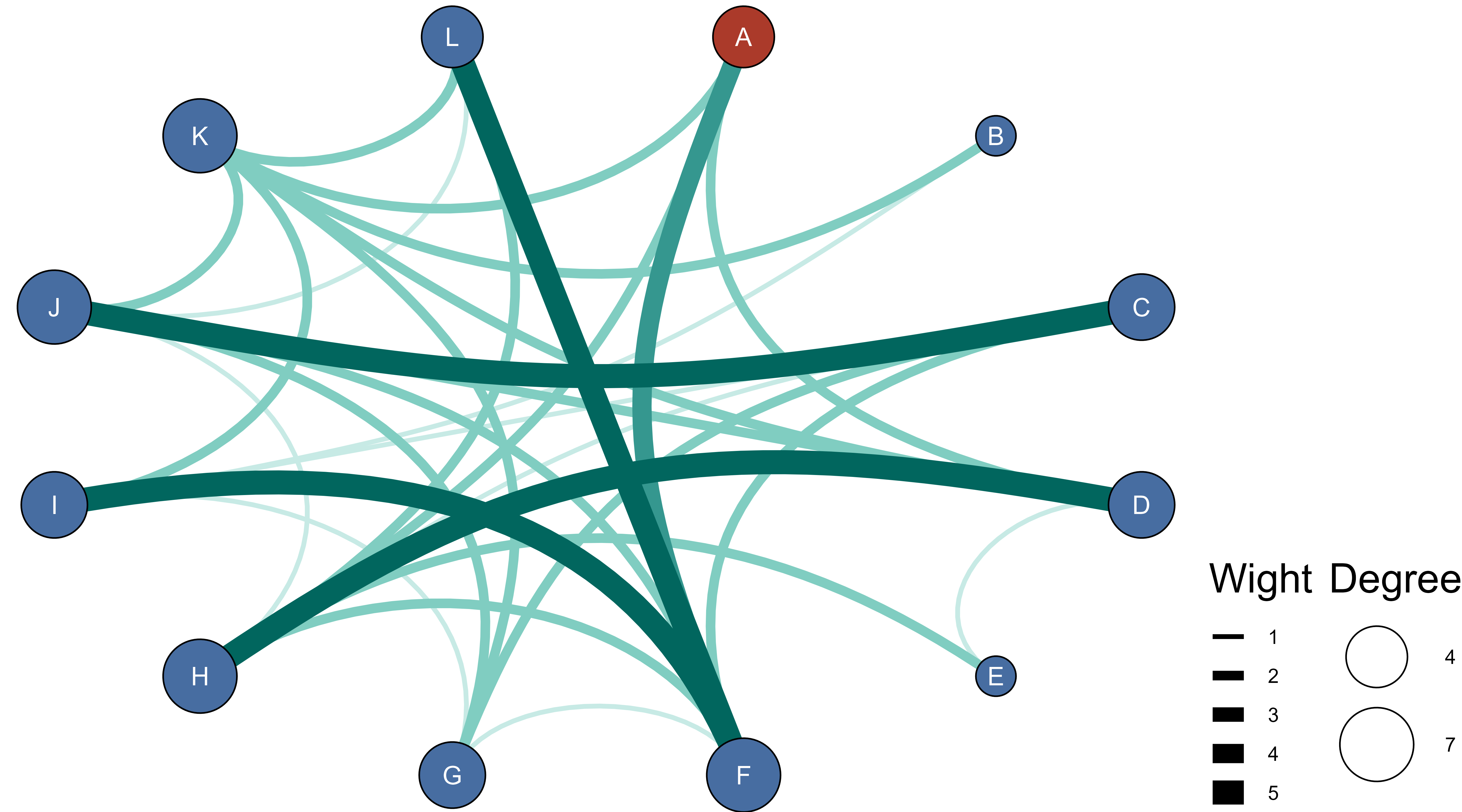
D3.js: 日历图
尝试了一些怎么用D3.js创建日历图,在前端训练营的道路上日行渐远hhh
以后要是有时间我觉得可以试试给我的博客添加一个日历图~

python库:d3blocks延续D3.js
| Block | Function | Blog |
|---|---|---|
| D3graph | d3.d3graph() |
D3graph |
| Elasticgraph | d3.elasticgraph() |
Elasticgraph |
| Sankey | d3.sankey() |
Sankey |
| Movingbubbles | d3.movingbubbles() |
Movingbubbles |
| Scatter | d3.scatter() |
Scatter |
| Heatmap | d3.heatmap() |
D3Blocks |
| Chord diagram | d3.chord() |
D3Blocks |
| Timeseries | d3.timeseries() |
D3Blocks |
| Image slider | d3.imageslider() |
D3Blocks |
| Violin plot | d3.violin() |
D3Blocks |
| Particles | d3.particles() |
D3Blocks |
| Treemap | d3.treemap() |
D3Blocks |
R包:Bayesplot可视化贝叶斯模型
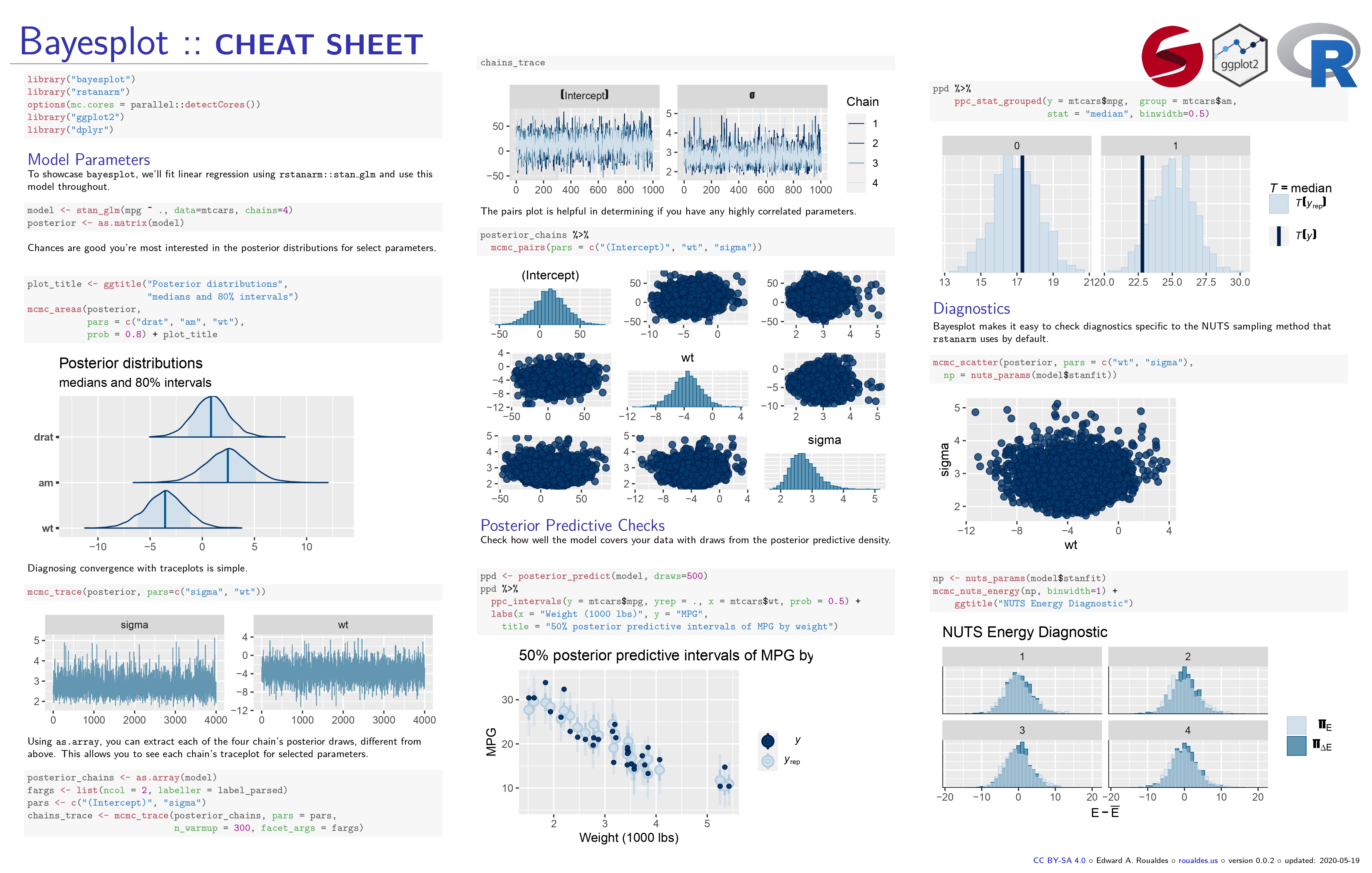
-
Schweitzer, F., Andres, G., Casiraghi, G., Gote, C., Roller, R., Scholtes, I., Vaccario, G., & Zingg, C. (2022). Modeling social resilience: Questions, answers, open problems (arXiv:2301.00183). arXiv. http://arxiv.org/abs/2301.00183 ↩
-
Amico, A., Verginer, L., Casiraghi, G., Vaccario, G., & Schweitzer, F. (2023). Adapting to Disruptions: Flexibility as a Pillar of Supply Chain Resilience (arXiv:2304.05290). arXiv. http://arxiv.org/abs/2304.05290 ↩
-
Zingg, C., von Gernler, A., Arzig, C., Schweitzer, F., & Gote, C. (2023). Detecting and Optimising Team Interactions in Software Development (arXiv:2302.14609). arXiv. http://arxiv.org/abs/2302.14609 ↩