日常 消费者行为 数据科学 深度学习 可视化

【阅】本周阅读摘选2023-05-01 → 2023-05-07

Posted by Cao Zihang on May 8, 2023 Word Count:
本周阅读摘选
2023-05-01 → 2023-05-07
目录

学术相关

Nature丨 Integrating explanation and prediction in computational social science1

在过去的15年中，社会科学经历了由网络技术革命带来的“计算革命”。随着计算机科学方法和实践的流入，社会科学需要处理大量的具有更多噪声、更非结构化且更少被设计的社会科学数据，并基于此产生了一个被称之为“计算社会科学”的新领域。

然而，这里产生了一个社会学家和计算机科学家在认识论上的紧张关系——社会科学家对个体和集体行为生成满意解释，特别是因果机制的传统；计算科学家优先开发精准预测模型，把可解释性放在次位的传统。

两种观点都产生了大量的成果，但同时也都受到大量批评。理论驱动的实证社会科学难以复制、难以推广、难以预测，也不能为现实问题提出解决方案；复杂的预测模型同样难以推广，而且不可解释，存在偏差。

作者认为两种观点在实践中存在整合的可能，并指出了一些整合两种观点的现有方法。其次，作者提出了一些可能产生更多整合模型的建议。此外，作者主张对解释和预测进行清晰标注，并认为开放科学的做法应该标准化。

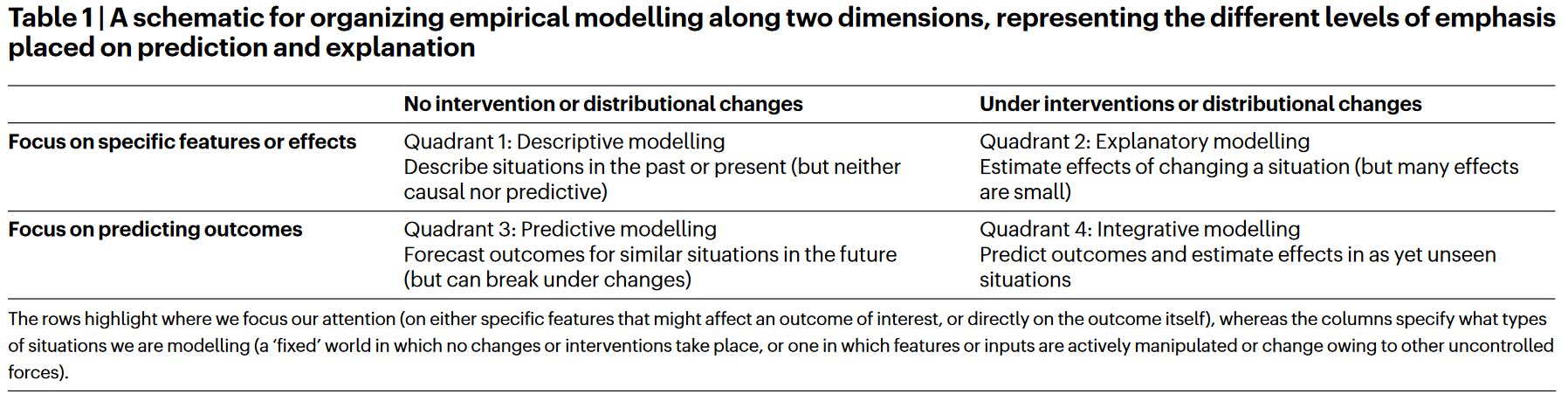
image-20230706225434564

在第四象限中，理想的整合模型能够对一个变化（干预等）的世界作出高质量的预测，因此它必须结合解释和预测才能处理一些极端的情境。然而，强迫解释去预测可能会发现这些理论所解释的比我们希望的要少，这会驱动人们去寻找更优的解释，但也可能会揭示出预测存在由系统复杂性或内在随机性产生的基本限制。

从这表格整体上来讲，第一、二、三象限囊括了几乎所有的传统的和计算社会科学研究，而第四象限除了个别例外接近空白。

基于此，作者给出3个建议：

  • 通过勾勒第四象限具体研究方法，使整合解释和预测模型的呼吁更具体
    • 在预测被操纵或分布变化的情境下测试现有方法的通用性
    • 通过跨领域或跨分布的模型测试，加强模型鲁棒性检验
    • 第二象限（解释模型）可以通过机器学习的方法改进现有解释技术的因果估计
    • 第三象限（预测模型）可以利用因果模型提高预测模型的可推广性
  • 主张建立明确的标签系统，确定研究所属象限和颗粒度水平
  • 在解释性建模群体中发展起来的开放科学实践可以被调整为有利于预测型建模群体
    • 预注册
      • 解释性建模社群→预测性建模社群
    • 通用任务框架
      • 验证数据集、评价指标、竞赛等
      • 预测性建模社群→解释性建模社群

image-20230707163651419

研究分享丨网络世界里的距离真的死了吗？ 地理距离对电子口碑效果的调节作用2

image-20230703003005168

主题 Title Author Journal ROF SPL CPL
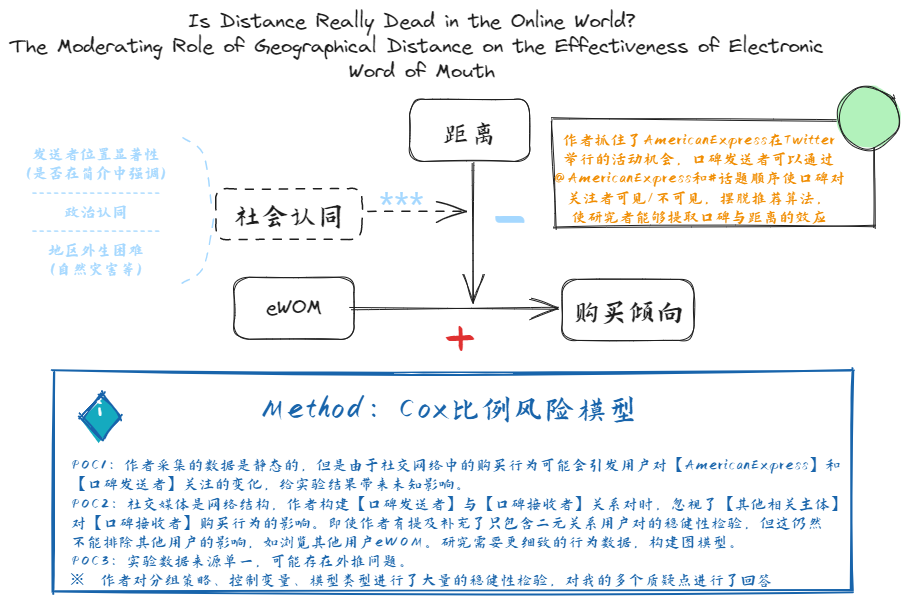
社会化媒体营销 Is Distance Really Dead in the Online World? The Moderating Role of Geographical Distance on the Effectiveness of Electronic Word of Mouth (Todri, V., Adamopoulos, P. (Panos), & Andrews, M.;undefined) JM 地理距离在数字世界（eWOM）中依然起到重要影响作用， WOM撰写者与接收者减少10英里的距离能增强eWOM 12.78%的效果 一些学者和业界从业者认为数字世界“距离已死”；也有人认为由于经济/相似向等因素，距离依然重要 前人研究数据过于粗糙，实验设计可能遮掩距离的作用或没有直接研究距离对eWOM效果影响
GAP RFW POC/RPP IV DV Method
现有研究缺少距离对eWOM效果影响的直接研究和“距离已死”争议的实证证据 1.需要测试其他背景 2.缺少操纵实验 3.机制解释需要进一步验证 4.数据需要更多行为变量 1.作者采集的数据是静态的，但是由于社交网络中的购买行为可能会引发用户对【AmericanExpress】和【口碑发送者】关注的变化，给实验结果带来未知影响。 2.社交媒体是网络结构，作者构建【口碑发送者】与【口碑接收者】关系对时，忽视了【其他相关主体】对【口碑接收者】购买行为的影响。即使作者有提及补充了只包含二元关系用户对的稳健性检验，但这仍然不能排除其他用户的影响，如浏览其他用户eWOM。或许需要更细致的行为数据，构建图模型。 3.实验数据来源单一，可能存在外推问题。 WOM，距离 购买倾向 Cox比例风险模型

放弃反向传播后，Geoffrey Hinton参与的前向梯度学习重磅研究来了3

代码

前向梯度学习作为深度神经网络中反向传播算法的替代品，能够计算出带有噪声的方向梯度。然而，标准的前向梯度算法在处理参数较多的模型时，会产生很大的方差。本文证明了通过扰动激活而非扰动权重的方式，显著地降低前向梯度估计的方差。同时，作者通过引入大量的局部贪婪损失函数（仅包含少量的可学习参数与适合局部学习的LocalMixer框架），扩展了前向梯度学习的可延展性。

反向传播算法虽然在过往取得了大量的成就，然而它被视作是生物学上不可能的结构，从工程学角度上，反向传播算法不符合大规模模型并行运算且限制了硬件设计。

文献综述

  • 前向梯度与强化学习

本研究基于Wenger在1964年提出的前向自动微分算法（AD），它在计算实际梯度时需要计算完整的Jacobian矩阵，因此会消耗大量的计算资源。近年，Baydin et al. 和 Silve et al.在与强化学习、进化算法有关的算法系列中发现，AD对于小规模问题来说是足够用的。

  • 局部贪婪学习

目前已有许多通过局部贪婪学习方法训练深度神经网络。例如，逐层贪婪预训练在一层或一个模块寻找贪婪最优。局部损失函数通常应用于不同层或残差阶段。

  • 不对称反馈权重

反向传播算法依赖于权重对称，但近期研究开始质疑这一约束。

  • 扰动学习

作者表明激活扰动比权重扰动具有更低的梯度估计方差。

前向梯度学习

前向自动微分算法AD

令$f:\mathbb{R}^m\to\mathbb{R}^n$，$f$的$n \times m$Jacobian矩阵为$J_f$。AD算法计算矩阵-向量乘积$J_f\mathbf{v}$，其中$\mathbf{v}\in\mathbb{R}^m$，作为$x$处估计的沿$\mathbf{v}$的方向梯度$J_f\mathbf{v}:=\lim\limits_{\delta\to0}\frac{f(x+\delta\mathbf{v})-f(x)}{\delta}$。相比之下，反向自动微分算法计算向量-Jacobian乘积$\mathbf{v}J_f$，其中$\mathbf{v}\in\mathbb{R}^n$。

与反向自动微分相比，前向自动微分只需要一次前向传递，并通过添加导数信息进行增强。

权重扰动前向梯度与激活扰动前向梯度

  • 激活扰动前向梯度

令$x_i$为第$i$个突触前神经元的活性，$z_j$为第$j$个非线性激活函数前的突触后神经元，$u_j$为$z_j$的扰动。激活扰动前向梯度估计$g_a(w_{ij})=x_i(\sum\limits_{j’}\bigtriangledown z_{j’}u_{j’})u_j$，其中$\bigtriangledown z$和$u$的内积通过前向自动微分计算。

image-20230708215231729

局部损失的放缩

扰动学习面临着一个维度的诅咒问题：随着扰动的维度数量增长，方差会随之增长，而在深度学习中这一问题会非常严重。降低这一问题影响的一种方式是通过将深度神经网络划分为多个子模块限制哦可学习维度的数量。

  • 块损失 Blockwise Loss

作者将深度网络在深度上划分为多个模块，每个模块包含多个层。每个模块的末端，算法会计算一个损失函数来更新模块内的参数。

这相当于在模块间添加一个停止梯度连接器。

  • 图像块损失 Patchwise Loss

在图像等具有空间维度的输入中，作者采用了一个空间维度上的独立损失，并分享权重。

  • 分组损失 Groupwise Loss

在通道尺度上，为创建多个损失，作者将所有的通道分割为多个组，每组附加一个损失函数。为阻止不同组之间的沟通，通道仅在同一组中与其他通道连接。

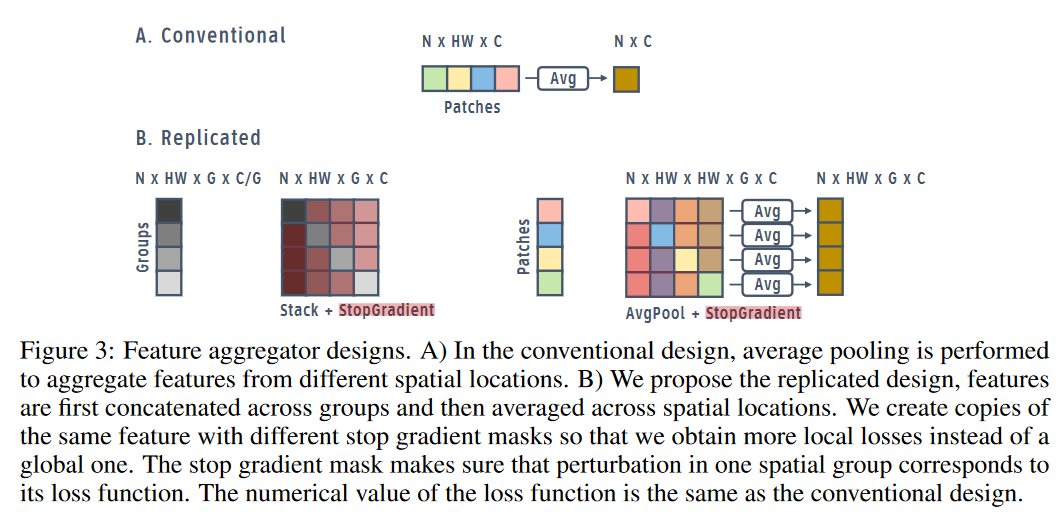
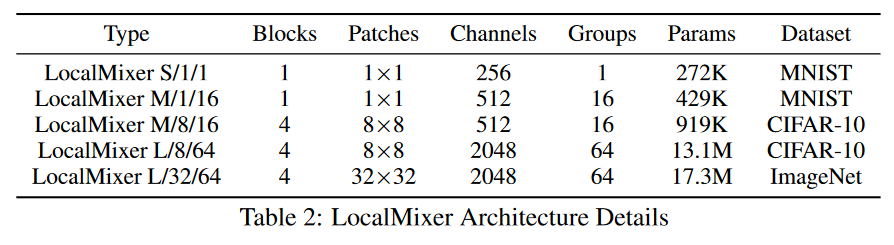
考虑到目前的设计缺乏全局信息，同时作者希望在不降维的前提下实现，因此作者设计了Figure 3的方式。各通道组被复制并相互交流，但在计算停止梯度时，除激活组外其他组均被遮掩以免影响前向梯度计算$X_{p,g}=[StopGrad(x_{p,1},…,x_{p,g-1}),x_{p,g},StopGrad(x_{p,g+1},…,x_{p,G})]$，其中$p$和$g$分别为patches和groups的索引。

相似的，每个空间位置也被复制、交流、遮掩并局部聚合$\bar{\mathbf{x}}_{p,g}=\frac{1}{P}(\mathbf{x}_{p,g}+\sum\limits_{p’\neq p}StopGrad(\mathbf{x}_{p’,g}))$。

image-20230708231612512

学习目标

对于监督分类问题，作者在聚合的特征之上添加了一个共享的线性层（在$p,g$之间共享）来获得交叉熵损失$L_{p,g}^s=-\sum\limits_{k}t_k\ log\ softmax(W_l\bar{\mathbf{x}}_{p,g})_k$。该损失在每个组和图像块位置上取得相同值。

实践

  • 网络架构

作者提出了对局部学习更适合的LocalMixer框架。

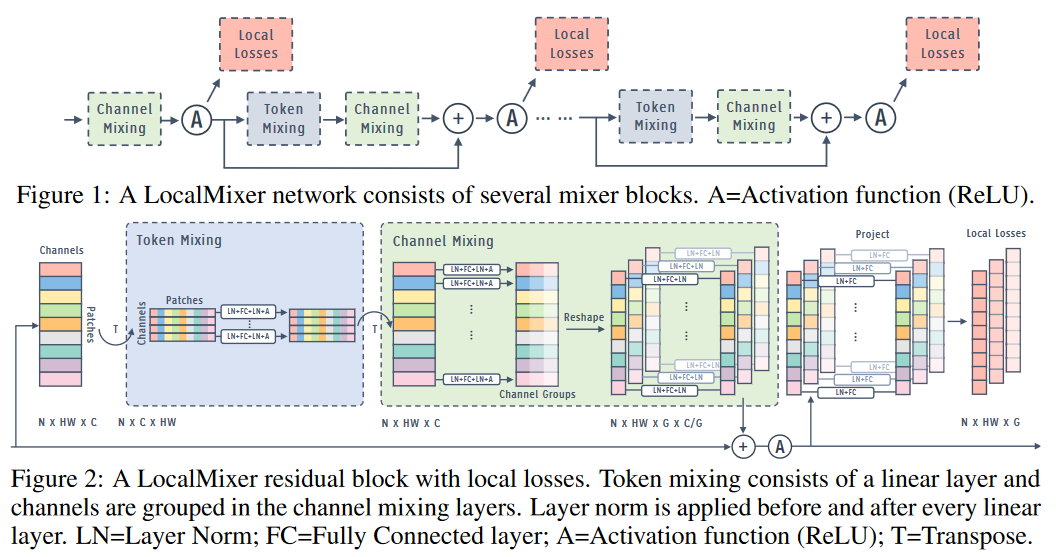
image-20230709122717226

image-20230709122736298

  • 正则化

作者选择了一种局部的层归一化变体，使得每个局部空间图像块的特征单独归一化。对分组的多个线性层，每个组单独正则化。

  • 有效实施复制损失

作者设计了JAX JVP/VJP函数，高效地节约内存并快速计算复制损失。

实验

  • 基准与变体
    • 反向传播算法
      • Backprop (BP)
      • Local Backprop (L-BP)
      • Local Greedy Backprop (LG-BP)
    • 反馈对齐算法
      • Feedback Alignment (FA)
      • Local Feedback Alignment (L-FA)
      • Local Greedy Feedback Alignment (LG-FA)
      • Direct Feedback Alignment (DFA)
    • 前向梯度算法
      • Weight-Perturbed Forward Gradient (FG-W)
      • Local Greedy Weight-Perturbed Forward Gradient (LG-FG-W)
      • Activity-Perturbed Forward Gradient (FG-A)
      • Local Greedy Activity-Perturbed Forward Gradient (LG-FG-A)
  • 数据集
    • MNIST
    • CIFAR-10
    • ImageNet
      • 数据增强

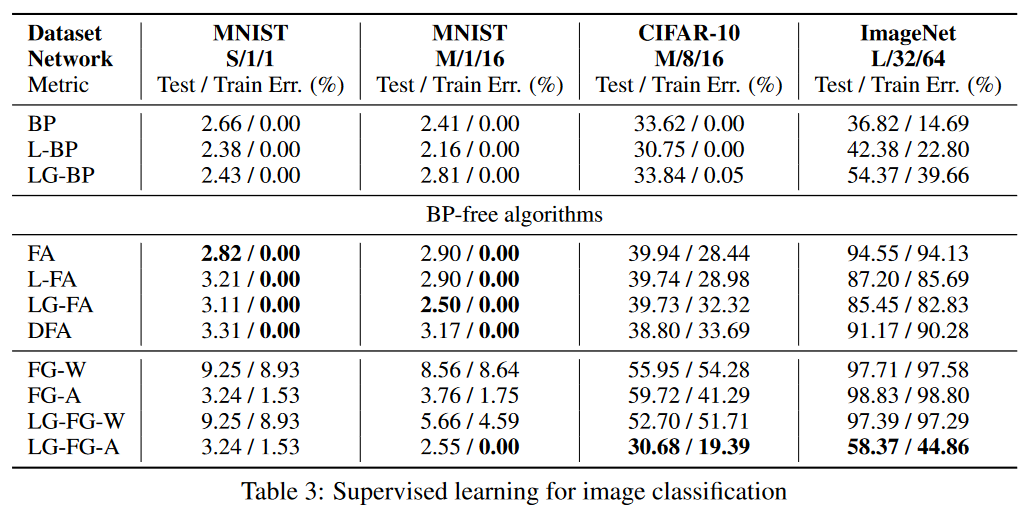
image-20230709130547549

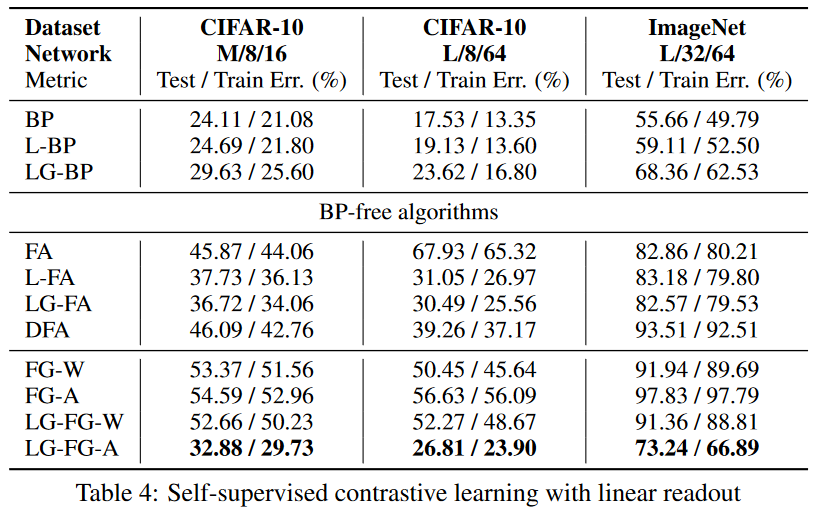
image-20230709130612439

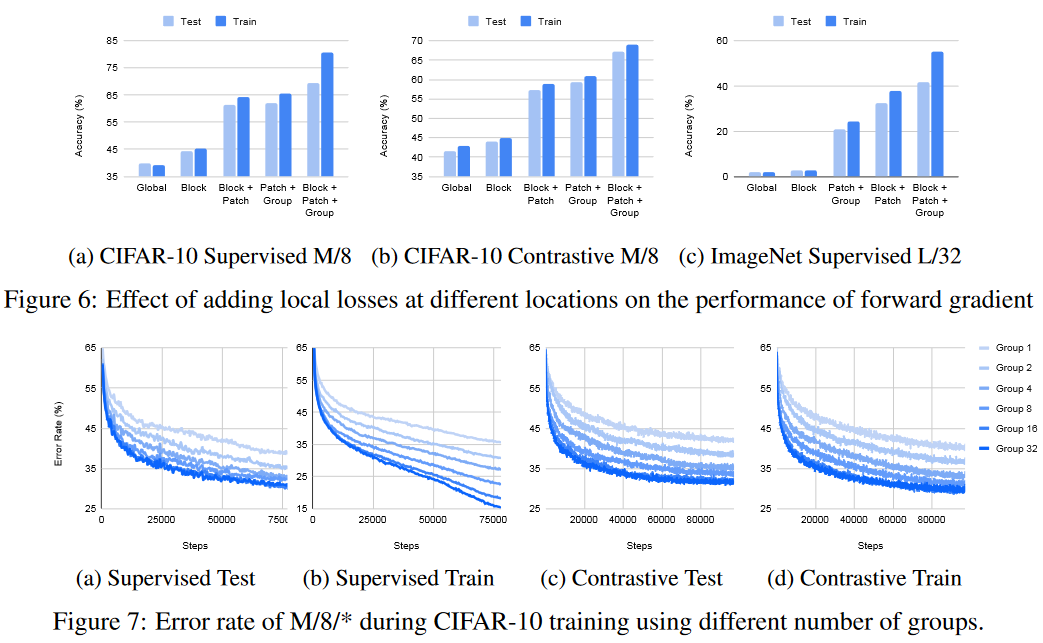
image-20230709130857075

结果表明，在监督学习中几乎没有引入局部贪婪损失的成本，作者提出的算法在MNIST和CIFAR上的测试误差与反向传播相似，但由于前向传播训练集不能过拟合到0%，可能新的架构仍然存在方差问题。在CIFAR-10的对比学习中，作者的算法接近了反向传播的表现。然而，随着问题越来越复杂，需要越来越多的层间合作，贪婪造成的误差也越来越大。

整体实验表明，作者提出的方法仍然与反向传播算法存在显著差距，但与没有反向传播算法相比，该前向传播算法已经进步很多。

技术 技巧

归一化混淆矩阵—normalized confusion matrix

img

image-20230523204748677

ggplot 绘图设置主题

ggplot2默认主题

  • theme_bw

951ba807-0064-4eaa-8cef-0f3ee5ad4e1f

  • theme_minimal

minimal

  • theme_classic

classic

  • theme_grey

grey

ggthemes

  • theme_excel

excel

  • theme_economist

economist

  • theme_fivethirtyeight

fivethirtyeight

  • theme_tufte

tufte

  • theme_gdocs

gdocs

  • theme_hc(style=’darkunica’)

hc_darkunica

  • theme_solarized

solarized

  • theme_solarized(light=False)

solarized_dark

  • theme_stata

stata

  • theme_wsj

wsj

hrbrthemes

  • theme_ipsum

ipsum

  • theme_mordern_rc

mordern_rc

  • theme_ft_rc

ft_rc

修改字体：showtext库

  1. Hofman, J. M., Watts, D. J., Athey, S., Garip, F., Griffiths, T. L., Kleinberg, J., Margetts, H., Mullainathan, S., Salganik, M. J., Vazire, S., Vespignani, A., & Yarkoni, T. (2021). Integrating explanation and prediction in computational social science. Nature, 595(7866), Article 7866. https://doi.org/10.1038/s41586-021-03659-0 ↩

  2. Todri, V., Adamopoulos, P. (Panos), & Andrews, M. (2022). Is Distance Really Dead in the Online World? The Moderating Role of Geographical Distance on the Effectiveness of Electronic Word of Mouth. Journal of Marketing, 86(4), 118–140. https://doi.org/10.1177/00222429211034414 ↩

  3. Ren, M., Kornblith, S., Liao, R., & Hinton, G. (2022, October 7). Scaling Forward Gradient With Local Losses. ArXiv.Org. https://arxiv.org/abs/2210.03310v3 ↩

CATALOG
    FEATURED TAGS
    消费者行为 日常 深度学习 学习笔记 可视化 数智化营销 复杂科学 市场调研 研究方法 世界趋势 仿真与决策 LLMs 数据科学 日常工具 机器学习 资料 AB测试 供应链管理 城市科学 推荐系统