学术相关
控制具有复杂节点的复杂网络1
现实世界网络中通常具有超过百万级别的交互异质节点,为解释这些真实世界系统,我们需要整合统计物理学和控制论的研究,并结合理论模型、机器学习即数据驱动控制方法,构建新的范式。
统计物理学主要关注的是元素集合的均衡、宏观特性,并为理解和预测大量简单同质化实体的集体行为提供了一个框架。控制论与之相反,它演进成为了动态系统和工程学的一个分枝,致力于寻求让系统或设备稳定地自发表现出适当的行为,并能够抵抗噪声、延迟和扰动的干扰。控制论关注的是设计反馈策略,进而引导相关系统的演化方向,在理想状况下,这种影响是通过改变相对较少的微观自由度实现的。
由于现实世界中,完全知悉、控制每个自由度及其交互通常是不现实的,因此我们需要进行微观与宏观,均衡与动态方法的协作,才能够处理具有复杂节点的复杂网络。这里的复杂节点表明每个元素都具有非线性行为,复杂网络代表异质元素之间存在复杂连接模式。
作者重点使用了两个控制论概念:可控性(是否存在控制输入可以在有限时间内仅使用特定允许操作将系统从任何初始状态引导至任何期望的最终状态)和可观察性(通过测量输入输入,估计系统内部状态的能力)。
文献综述
统计物理学
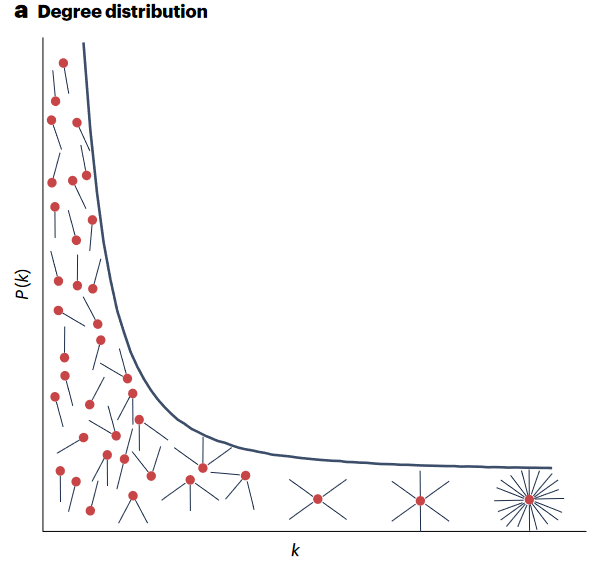
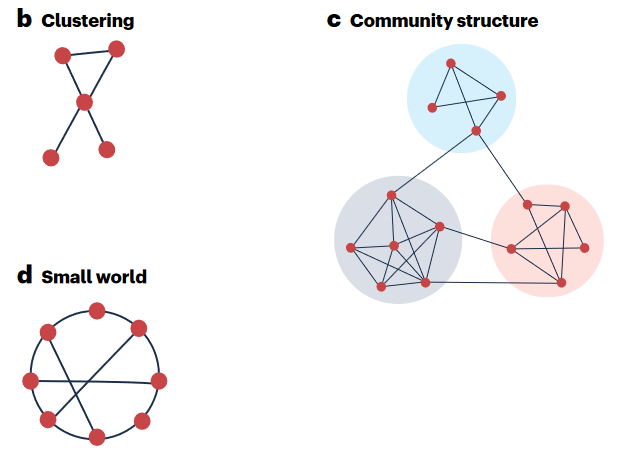
上世纪90年代末,随着互联网的飞速发展,统计物理学的方法(如随机图模型、生成函数和速率方程)为理解复杂网络提供了许多洞见。这些方法通常将网络刻画为广泛的、跨越数量级的度分布,它的特点是对随机移除节点具有鲁棒性,但对针对性消除比较脆弱,也缺乏明确的传播阈值。除了度数分布外,小世界现象、模块化和三元闭环也是常见的网络特征。
|
|
|
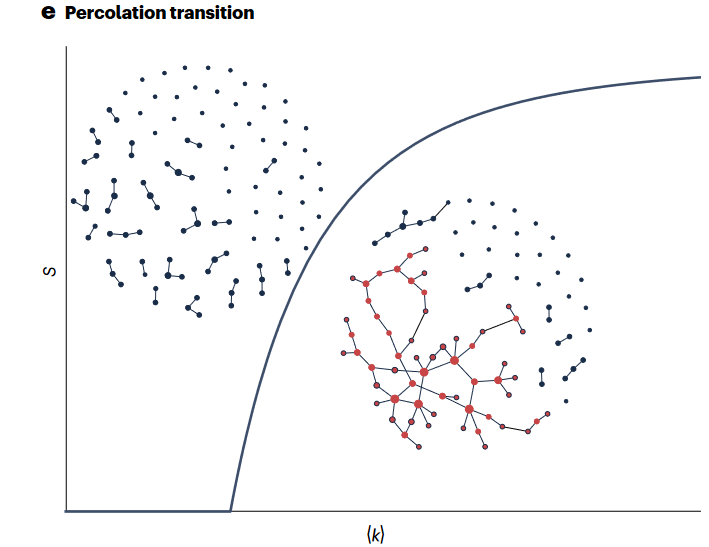
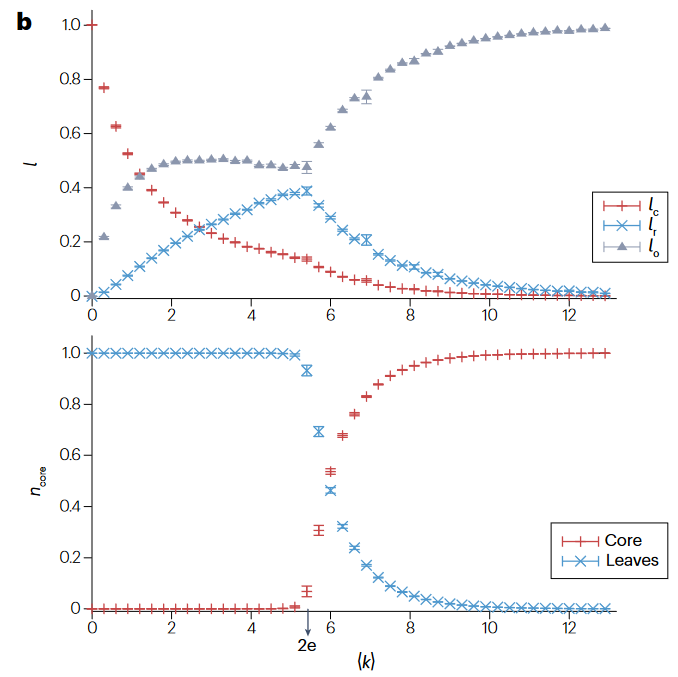
2011年,一项关于具有线性动力学和任意度分布网络集合的可控性研究建立了统计物理与复杂网络控制之间的连接。这一连接建立于70年代,在线性动力学网络中通过图论解决控制问题的结构控制框架,它试图解决将控制输入作用于驱动节点(driver nodes)能否在有限时间内将网络从初始状态转变为期望的最终状态。这一研究最关键的洞见是将最小驱动节点集合识别问题映射到网络最大化匹配问题,并通过统计物理学的空腔方法解决。
|
|

|
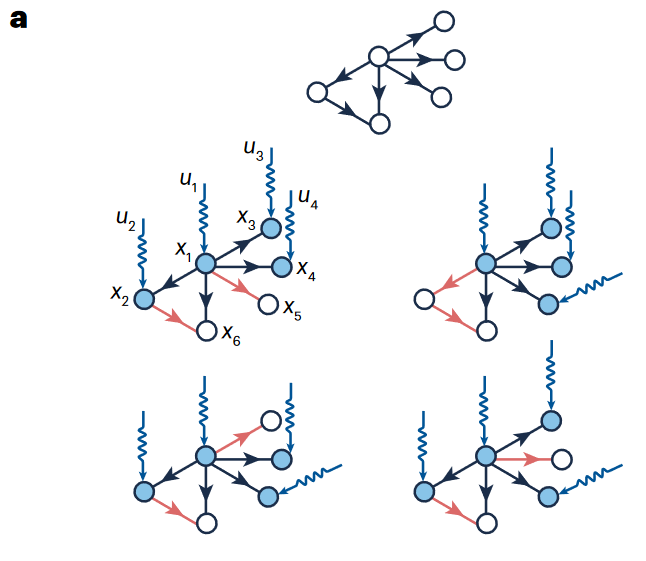
在结构控制中,我们只关注结构,忽略权重。传统的结构控制框架假定节点根据线性时变动力学进行演化$\dot{\mathbf{x}}=A\mathbf{x}(t)+B\mathbf{u}(t)$。该特性意味着线性代数工具可以用于阐明网络结构与可控性的联系。
除了结构控制,现有研究也发展了控制能(control energy)、控制配置(基于控制流模式)、现实世界约束等方向。作者提名了几篇相关重要综述。
目前,问题是如何将统计物理学方法扩展至动态、非均衡、非线性系统。
控制论
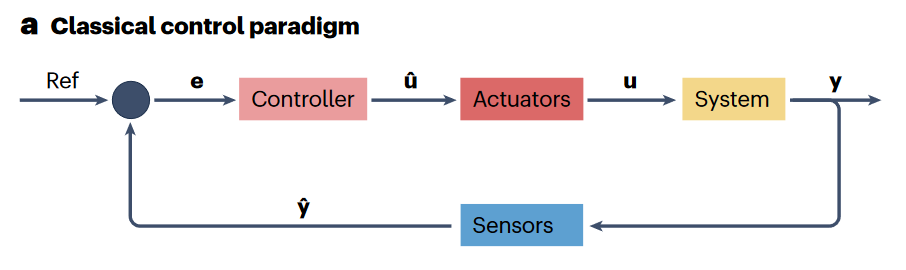
经典的控制论范式,通常起始于系统结构和动力学的数学表示,并包含合成反馈控制策略。负反馈机制提供了稳定行为的能力,正反馈则可以用于非线性系统中双稳定性和分叉。
目前,控制论已经发展了许多类的线性/非线性系统及其控制策略的数学化表示,这些方法通常是分布式和/或去中心化的,其中一些应用了复杂的非线性、自适应、可计算和时变方法。
控制论的研究很大程度上聚焦于独立系统,即所有相关的自由度、动力学和耦合均为已知信息。因此,这样的经典范式通常受到表现为通过复杂交互网络互作的大规模动态系统集群的新兴应用的挑战。目前,这种复杂网络的控制越发成为控制论的核心问题。
|
|

|
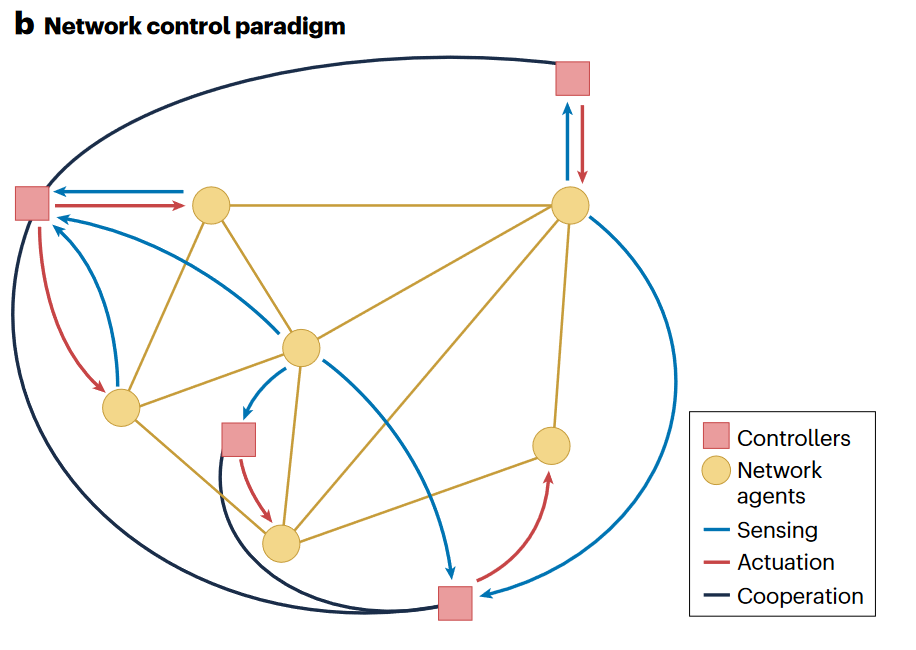
从控制论的观点分析复杂网络问题,关键就变成了给定一个网络,它是否满足可控性和可观察性这些基本控制属性,以及如何在不同尺度上(宏观行为的反馈连接需求;微观级别的控制行为需求)实现闭环反馈。控制的实现可以使用操控网络中特定节点、赋予边动力学/交互协定、操纵网络自身结构或综合方法。例如牵制控制(pinning control)通过操控小比例的网络节点或边实现对系统集体行为的控制。
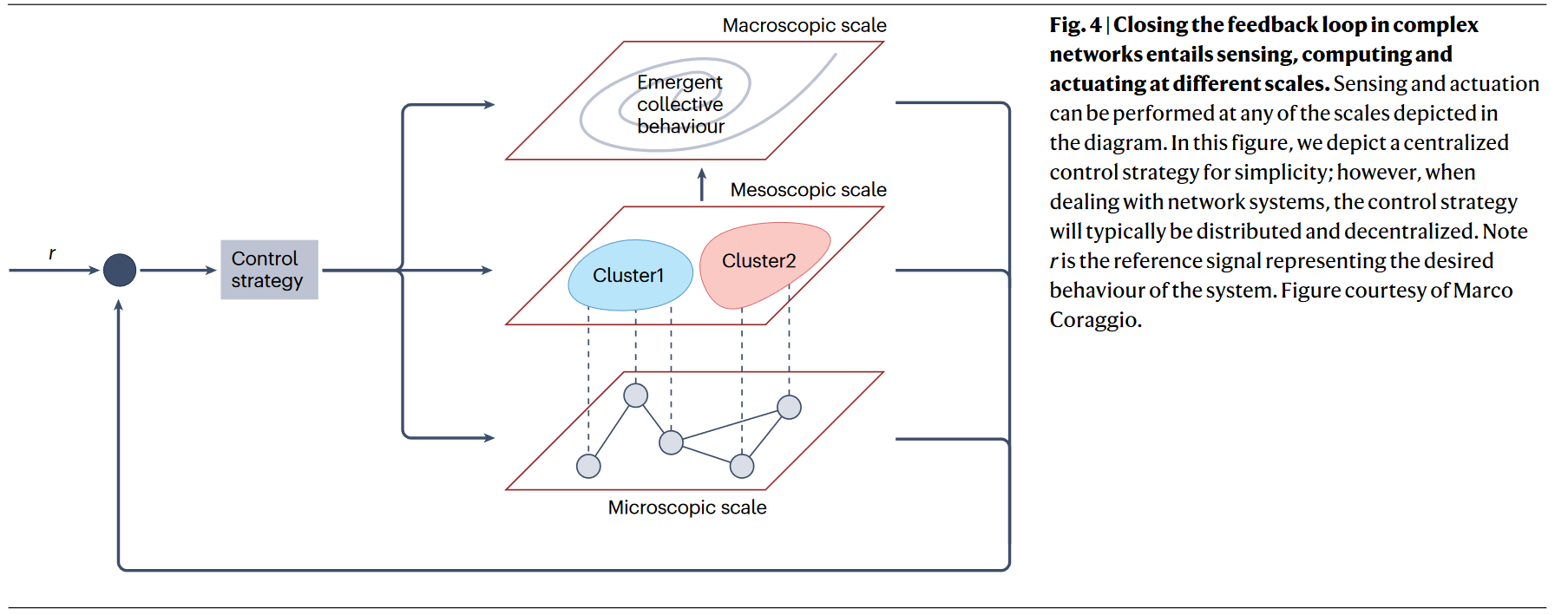
控制现实世界网络存在着一些重要挑战。现实世界网络存在多种长度尺度和时间尺度下的行为与交互,包括个体间互作的自组织行为。网络本身也可能是模糊的,由于成本约束有时无法学习完整的连接模式,可能会对模型产生显著影响,此外网络的动力学活动和拓扑结构同样重要。 异质性和多重尺度也意味着不同的系统环节可能需要不同类型的表示。
建模的关键问题是测量哪些元素,要影响哪些元素,什么时候以及如何施加影响,此外研究如何收敛至期望行为及控制策略保持对复杂网络的鲁棒性和韧性的方法也至关重要。
现有建模范式
统计物理学方法
统计物理学的概念和技术被大量应用于复杂网络结构和动力学属性的研究,研究领域包含网络生长、相变和级联故障。
| 概念/方法 | 概述 | 应用 |
|---|---|---|
| 统计综述 Statistical ensemble | 综合考虑系统的一组(无限多)虚拟复制,每个复制表示真实系统的一种可能配置 | 随机图模型的持续发展 |
| 母函数形式 Generating function formalism | 基于分支过程和树假设的平均场方法 | 网络结构、动力学和(树状网络)特定控制属性 |
| 主方程方法 Master-equation approach | 系统的时间演变由决定状态转换的转移速率矩阵 | 生长网络的结构 |
| 速率方程方法 Rate-equation approach | 适用于多种非平衡现象,如聚集、粗粒化和外延表明生长 | 生长网络的结果 |
| 自组织临界 Self-organized criticality | 具有作为吸引子的临界点的系统,它无需控制参数调整就表现出临街性 | 网络系统的级联故障 |
| 空腔法 Cavity method | 为解决无序系统(如自旋玻璃)等统计物理中的平均场类模型发展的数学方法 | 在结构控制框架下检验复杂网络的控制属性 |
控制论方法
控制问题可以被概括为确立感知对象,确立控制对象及利用感知信息实现期望目标的手段。因此,任何控制设计都会包含感知、计算和驱动三要素。
| 概念/方法 | 概述 | 应用 |
|---|---|---|
| 线性/非线性可控可感准则 | 如卡尔曼准则、结构可控可感和非线性可控可感 | 从复杂网络中获取可控可感的图论准则 |
| 稳定性分析的Lyaponov直接法 | 通过使用Lyapunov方程扩展Lyaponov直接法分析网络系统稳定性 | 研究网络系统稳定性,包括研究全局横向稳定性、非线性一致性问题、牵制控制和连接稳定性 |
| 网络控制设计工具的无源耗散系统理论和外部稳定性概念 | 在复杂网络中扩展无源耗散系统理论;定义与运用增量无源耗散概念 | 研究动态智能体互联并建立收敛性 |
| 线性/非线性控制方法 | 使用最优控制、自适应控制、智能控制、非线性控制、切换和混合控制以及比例积分微分控制 | 适用于工程到生命科学的各种不同应用 |
| 牵制控制 | 控制少数特定智能体操纵集体的宏观行为 | 为复杂网络一致性和同步性设计领导者-追随者策略 |
| 收缩理论和增量稳定性分析工具 | 使用微分稳定性工具研究复杂网络收敛性 | 证明相关网络系统收敛性 |
| 分布式协同控制方法 | 利用分布式和协作控制策略在网络系统中感知、驱动和控制 | 通过设计节点间交互协议,网络边与结构的自适应和演变,设计复杂网络中协作、一致和同步策略 |
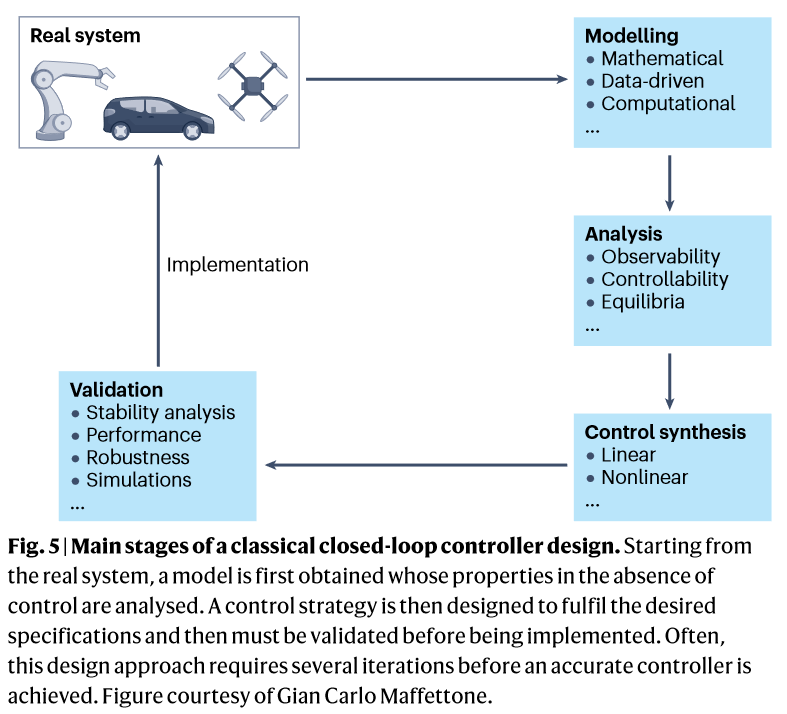
动力学系统方法
给定系统行为动力学方程模型及其由吸引子、极限环和吸引盆边界的相空间,可以找到利用自然轨迹将系统驱动到相空间理想区域的扰动策略。
新范式和建模技术
一些前沿的技术包括超图、单纯复形,定义统计综述,分析可接受的同步模型、完全同步和簇同步的稳定性与可控性。活动驱动时序网络的范式也富有成效。真实世界系统通常是多层网络形式,这一概念是多层网络结构控制,使用图论捕捉分层关键基础架构和多重控制策略的基础。
没看懂
研究指南
- 弥合学科差异,将平均场方法等技术的应用扩展到复杂网络控制,同时考虑现实约束条件及实现反馈策略的需求,保证稳定性、表现和鲁棒性
- 确立一系列范例问题或基准案例用于验证和对比不同的复杂系统控制方法
为此,作者呼吁发起类似ImageNet、Netflix等针对标准方法的挑战赛,而且由于复杂系统控制具有多学科性质,挑战不必拘泥于纯理论问题,也可以是应用或转化挑战。
技术技巧
Boruta算法:特征筛选
Boruta算法是2010年提出的一种基于随机森林的分类包装器算法,它用于排除模型中不重要的特征,选出所有与因变量相关的特征。
它的基本方法是将原始数据集中的特征随机打乱(shuffle)获取shadow特征,将shadow特征与原始数据集进行横向拼接,并使用模型对其进行训练,得到每个特征的特征重要性。Boruta认为如果一个特征是有效的,则它的特征重要性一定比随机版本好,因此Boruta保留原始特征重要性得分(z-score)明显高于随机版本的特征。
考虑到随机森林算法存在较大波动,Boruta会采用迭代策略取均值,并对原始特征与影子特征重要性大小关系进行统计检验(二项分布)。
清华大学彭皓:事件抽取分享
目前,知识图谱存储着大量世界知识,支撑着问答等诸多重要下游应用,但现有的知识图谱缺乏事件知识。常用的开源知识图谱中实体有千万级数量,而事件只有十万级。
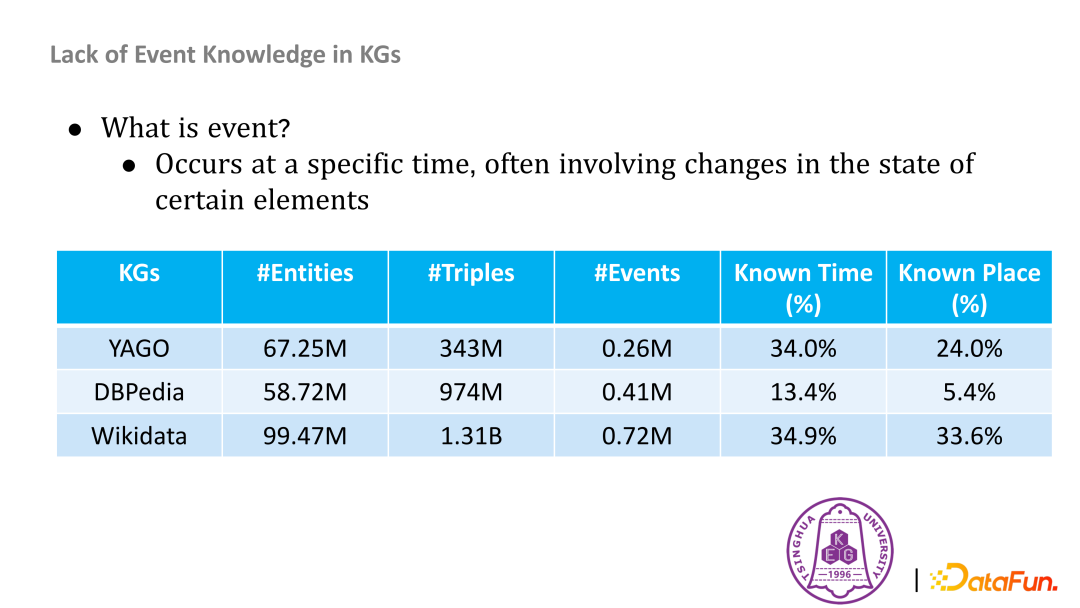
- 事件抽取
事件抽取指给定文本,从文本中抽取结构化的事件知识(事件是什么及相关信息等)。
事件抽取通常包括事件检测(给定文本,检测文本中包含的事件)和抽取事件相关信息(时间、地点、人物等)两个子任务。
- 事件抽取算法主流范式
① Sequence labeling 序列标注任务
将事件抽取问题形式化为一个序列标注任务,在指定文本中标注事件、相关论元
② Token Classification 词元分类任务
为每个词进行分类,分辨该词隶属于事件、论元还是NA类别
③ Machine Reading Comprehension 阅读理解任务
给定文本及事件相关问题,要求学习器回答问题
通常采用抽取文本区间的方式回答
④ Seq2seq 序列生成任务
分享者创建了一种包含多种事件抽取算法的工具包OmniEvent。
Python:Matplotlib速查表
内置主题——普遍不好看
娱乐
多尺度演化:竞争群体内部及之间的演化动力学2
作者扩展了进化博弈论用于描述多层进化动力学,使用嵌套生灭过程(nested birth-death processer)和偏微分方程建模个体在群体内部和群体之间的自然选择行为。作者使用这套理论分析了已知的促进单一群体内部合作机制如何在群体间竞争的情况下改变演变结果。作者发现,在多尺度系统中最有利于合作的个体结构可能与单一群组内最有利于合作的个体结构是不同的。对于具有连续策略范围的竞争性活动,群体间的选择可能无法产生社会最优结果,但可能产生次优方案平衡个体叛逃动机和群体合作动机。
对于群体竞争问题,目前,生物学家已经开发了研究群体内战略互动的稳健理论框架——进化博弈论。生物学家已经揭示了大量能够协调激励个体产生有利群体行为的激励机制,如激励、互动、人口结构或互惠,这些机制可以在具有少量甚至没有认知能力的个体演化中涌现。即使在一组繁殖个体中,这些机制也能促进合作与协调,实现集体结果由于潜在博弈的纳什均衡状态。然而,这些机制除非对个体适应有足够强的影响才能成功地提高合作,有些机制可能只是将促进合作均衡作为稳定的、全防御者结果的替代方案。此外,这些通过个体选择促进合作的机制的数学模型并没有考虑群体之间的可能性和影响。
但幸运的是,进化博弈论可以在多个组织层级上同时描述自然选择过程,既刻画群体内个体竞争,又能刻画种群间个体竞争。这一特性为探索个体叛逃动机和集体合作动机的互作提供了一个框架, 突出了进化过程中不同层次选择间的角力。
本文综合了近期多尺度进化博弈论的发展,系统性对比了单一群组与多尺度竞争的结果差异。本研发现单一群组内部的长期竞争结果(甚至包含分类、互惠)与同步的多群组内、外竞争结果存在量化差异。本文进一步地综合了群内机制(分配、互惠、种群结构)效应与群间竞争效应,发现在多数情境下两种效应在促进集体利益上存在协同效应。
通用模型框架
- 博弈论中的交互
我们首先考虑多组能够与他们同群组成员互动的个体,每个具有两种可能策略:合作$C$或叛逃$D$。一般地,在包含$x$比例合作者的群组,合作者的出生率为$\pi_C(x)$,叛逃者出生率$\pi_{D}(x)$,对任意函数$\pi_C$和$\pi_D$满足$\pi_D(x)>\pi_C(x)$。
作者采用复制方程 (replicator equation)刻画大总体中的个体层级选择来描述演化行为。复制方程依据繁殖率追踪了群组合作者比例$x$随时间变化的轨迹$\frac{dx}{dt}=x(1-x)(\pi_C(x)-\pi_D(x))$。这一复制方程既可以通过自然选择的繁殖竞争模型推导,也可以通过个体决策的社会学习模型中推导。
本研究的多数分析适用于满足任意出生率的$C$和$D$,但为了研究合作本身,作者将聚焦于合作者具有$c>0$成本并给对手带来$b>0$收益,而叛逃者没有成本也不带来收益的合作博弈,同时假定双方合作会产生$d$的潜在额外协同效应收益(可正可负)。合作博弈的损益矩阵为$\begin{align}C\\ D\end{align}\begin{pmatrix}b-c+d&-c\\ b&0\end{pmatrix}$。
个体的损益将决定他们的繁殖率。
对于拥有$x$比例合作者的群组,合作者个体进行所有配对互动的平均损益为$\pi_C(x)=(b+d)x-c$,叛逃者的平均损益为$\pi_D(x)=bx$,因而群组全体成员的平均损益为$G(x)=(b-c)x+dx^2$。
当$b>b-c+d>0>-c$时,即$c>d>c-b$,该合作博弈满足囚徒博弈情形。当$c>d$时,$\pi_D(x)>\pi_c(x)$对$\forall x\in[0,1]$恒成立。
若$d<0$,则有$c-b<0$,即$c<b$,所以群组的最佳合作者比例$x^\ast=\left\{\begin{align}&1,d\leq\frac{c-b}{2}\\ &\frac{c-b}{2d},d>\frac{c-b}{2}&\end{align}\right .$
(预设一种情形,后面会提及)
将合作博弈代入复制模方程$\frac{dx}{dt}=x(1-x)(\pi_C(x)-\pi_D(x))=x(1-x)(dx-c)$。由于$d<c$,这意味着在PD game中合作水平永远下降,在长期会收敛于全部叛逃的情形。
- 多水平选择嵌套模型
为研究多层级水平选择下的策略行为演化,作者采用上述方法构建了多个群组。除了组内个体繁殖差异引起的组内策略变化,作者还设定当一组决定模仿其他组策略情境(亦即一组死亡,一组繁殖)下的组间动态性。
作者采用如图所示方法表示个体水平和群组水平的生灭事件。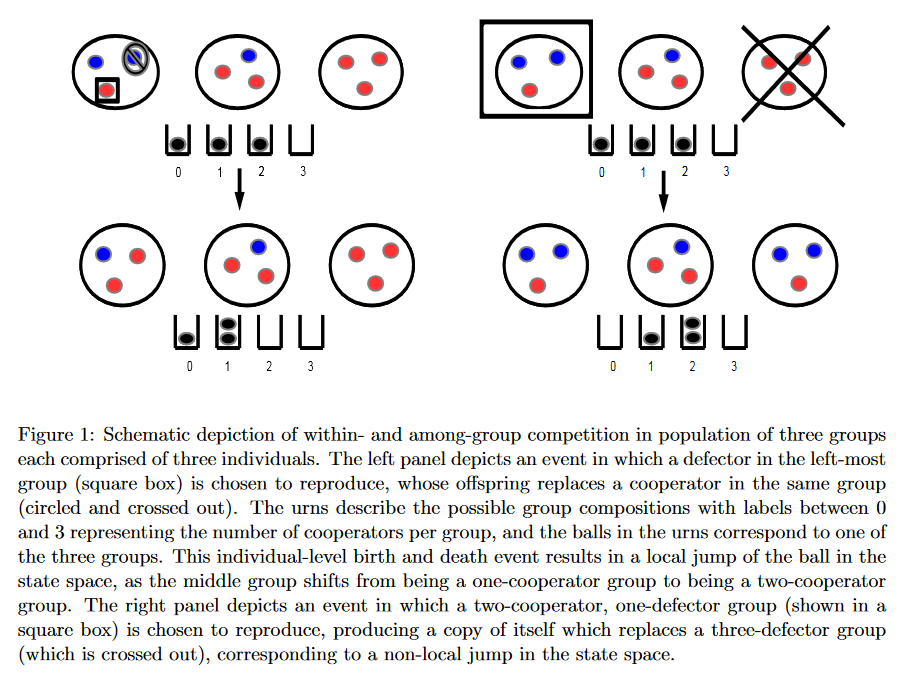
- 无限多大群组偏微分方程极限
作者使用偏微分方程描述了在时间$t$无限个群组包含的合作者比例$x$的演化概率密度函数$\frac{\partial f(t,x)}{\partial t}=-\overbrace{\frac{\partial}{\partial x}(x(1-x)(\pi_C(x)-\pi_D(x))f(t,x))}^{组内竞争}+\lambda \underbrace{f(t,x)[G(x)-\int_0^1 G(y)f(t,y)dy]}_{组间竞争}$
$\int_0^1G(y)f(t,y)dy$为整体的平均损益。方程的第一项促使每个群组走向全部叛逃的囚徒困境(或其他混合合作与叛逃的稳定博弈,如鹰鸽博弈),第二项偏好高于平均水平的损益,参数$\lambda$衡量了组内与组间竞争的相对重要性。
这段没看懂,没有任何分形几何的知识orz
由于方程是一阶非局部双曲偏微分方程,因此可以使用特征线法分析。特征曲线相当于传统的复制方程,因此特征曲线描述了组内选择的影响,而沿特征的解追踪了组间选择的影响。
方程的长期行为解$f(t,x)$依赖于各群组策略比例的初始分布。特别地,动力学系统取决于接近全合作者均衡$x=1$情况下的初始分布密度,并通过$x=1$处$H\ddot{o}lder$指数$\theta$量化。在一定程度上,我们可以认为$\theta$大小与初始总体中高合作组的规模相反。
- 持续合作
组内选择在囚徒困境情境下倾向于导致个体叛逃,而组间选择能够提升群组合作。因此,当组间选择相对于组内选择对演化的影响$\lambda$超过一定阈值$\lambda^\ast$时,合作就可以长期存在。
本节研究的设计不仅仅适用于先前提及的合作博弈,同样适用于任意满足$\pi_{D}(x)>\pi_C(x)$和$G(1)>G(0)$(全合作收益大于全叛逃收益)。
当$\lambda>\lambda^\ast$时,$f(t,x)$会收敛于一个稳定的状态$f_\theta^{\lambda}(x)$,生成正向水平的合作,它的值依赖于$H\ddot{o}lder$指数$\theta$相关的初始密度。相反的,当$\lambda\leq \lambda^\ast$,在长期条件下所有群组都会变为全叛逃状态。
阈限的定义如下:
$\lambda^\ast:=\frac{(\overbrace{\pi_D(1)-\pi_C(1)}^{个体叛逃动机})\theta}{\underbrace{G(1)-G(0)}_{群组合作动机}}$
这一定义反映了持续合作的产生需要足够强度的组间选择来抗衡个体成为叛逃者的诱惑,此外阈值大小随$H\ddot{o}lder$指数$\theta$递增意味着初始全合作组占比越小的总体需要更强的组间竞争($\lambda$)来维持长期合作。
对于整体结果,当组间选择过弱$\lambda\leq\lambda^\ast$,所有的组群都收敛于全叛逃状态,因此整体平均损益为$G(0)$;当组间选择满足$\lambda>\lambda^\ast$时,平均总体损益在稳态密度$f_\theta^\lambda(x)$处收敛于$\langle G(\cdot)\rangle_{f_\theta^\lambda}=\int_0^1 G(x)f_\theta^\lambda(x)dx=G(1)-\frac{\theta}{\lambda}(\pi_D(1)-\pi_C(1))$。
因此,长期整体平均损益为$\mathop{lim}\limits_{t\to\infty}\langle G(\cdot)\rangle_{f_\theta^\lambda}=\left\{\begin{align}G(0)&, \lambda\leq\lambda^\ast\\ G(1)-\frac{\theta}{\lambda}(\pi_D(1)-\pi_C(1))&, \lambda>\lambda^\ast\end{align}\right.$
将$\lambda^\ast:=\frac{(\overbrace{\pi_D(1)-\pi_C(1)}^{个体叛逃动机})\theta}{\underbrace{G(1)-G(0)}_{群组合作动机}}$代入,消去$\theta$,可得$\mathop{lim}\limits_{t\to\infty}\langle G(\cdot)\rangle_{f_\theta^\lambda}=\left\{\begin{align}G(0)&, \lambda\leq\lambda^\ast\\ [\frac{\lambda}{\lambda^\ast}]G(0)+[1-\frac{\lambda^\ast}{\lambda}]G(1)&, \lambda>\lambda^\ast\end{align}\right.$
该结果意味着集体损益介于$G(0)$与$G(1)$之间,无限强的组间竞争导致的全合作状态是整体损益的上限。对于完全合作可以最大化群组损益的博弈,强大的组间竞争可以优化整体结果,但是如果群组损益$G(x)$最大化$x^\ast<1$(如前文案例),则任意强度组间竞争到不能实现整体最佳损益。
在一些博弈中,任何群体间竞争都不能抹去在有许多合作者的群组内,个体叛逃会获取优势的事实,作者将这一现象称之为次级选择的阴影。这一现象在集体水平依然明显,在组间竞争无限强的情况下,长期整体会收敛于存在一个低于社会最优合作水平的群组,但是他们却能获得与全合作群组完全一致的集体回报。
即从组内与组间竞争角度再次验证了free-rider。
除了无限数量群组情形,作者同样考虑了有限群组情形。在一个具有$m$个群组的集体中,每个群组包含$n$个个体,并假定组内竞争的作用速度是一个比组间竞争更快的时间度量。在同样的合作博弈损益情况下,作者发现如果群组水平和个体水平复制的选择强度比$W$超过阈值$W^\ast=\frac{n-1}{2(m-2)}(\frac{(\pi_D(1)-\pi_C(1)+(\pi_D(0)-\pi_C(0)))}{G(1)-G(0)})$,固定的合作水平会更有利。同样的$\frac{n-1}{2(m-2)}$反映了个体与群组水平刺激的拉锯战。
基于多水平选择的合作演化简单规则
上述结果表明,集体支持合作并达到高水平集体损益的能力依赖于组内/组间竞争相对强度$\lambda$、个体叛逃利益$\pi_D(1)-\pi_C(1)$、完全合作群组优势$G(1)$和单个群组内部最优合作水平$x^\ast$。
由于通过多水平选择支持合作的能力要求集体激励合作来对抗个体叛逃动机,因此本研究可以通过提升合作利益或降低叛逃优化来解释促进合作的生物学机制。
例如分类机制中,个体既有$r$概率与采用相同策略的个体互动,有$1-r$概率随机互动。
这些机制单独在个体水平或群组水平选择背景下均被前人研究过,作者定性地总结了他们的研究成果。
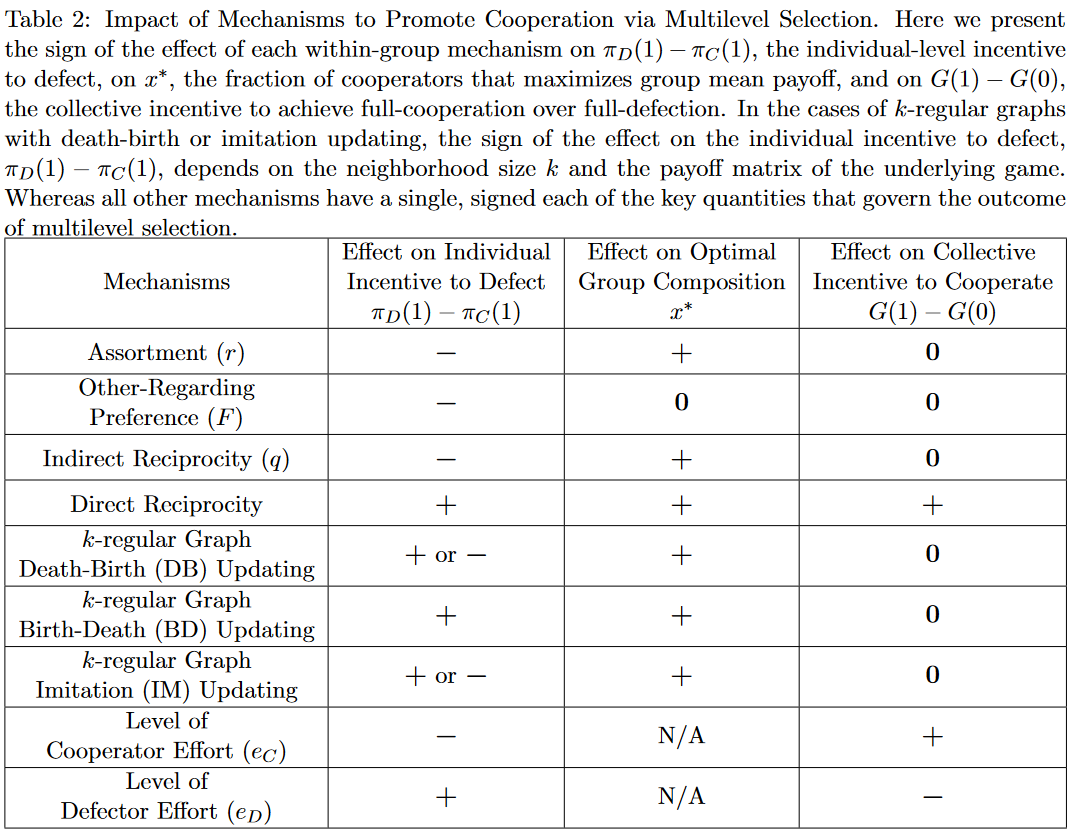
在定性研究基础上,作者借助前文的广义三参数囚徒困境背景下考虑量化效应。由$\begin{align}C\\ D\end{align}\begin{pmatrix}b-c+d&-c\\ b&0\end{pmatrix}$和$\lambda^\ast:=\frac{(\overbrace{\pi_D(1)-\pi_C(1)}^{个体叛逃动机})\theta}{\underbrace{G(1)-G(0)}_{群组合作动机}}$,$\lambda^\ast_{PD}=\frac{(c-d)\theta}{b-c+d}=(\frac{b}{b-c+d}-1)\theta$。
这表明选择水平阈值$\lambda^\ast_{PD}$是协同效应参数$d$的减函数,即越大的协同效应越容易通过多重选择实现合作。
将原情境简化为没有协同效应($d=0$)的简单博弈,<div style='width=80%'>$\begin{align}C\\ D\end{align}\begin{pmatrix}b-c&-c\\ b&0\end{pmatrix}$</div>。作者通过最小收益-开销比$\frac{b}{c}$来刻画这类博弈。

该结果表明多数机制可以通过多水平选择促进合作。例如like-with-like Assortment,收益-开销比促进合作的阈值$(\frac{b}{c})_{r,MS}^\ast$是分类概率$r$的减函数,$\frac{\partial}{\partial r}(\frac{b}{c})_{r,MS}^\ast=-\frac{\theta(\lambda+\theta)}{(\lambda+\theta r)^2}<0$。
具备网络互惠性的多水平选择:对近邻数量的非单调依赖
网络中的结构性互动对多水平选择的合作演化比分类/互惠相比有更细微的影响。
对于一个具有生灭更新规则(BD)的结构化总体,合作在个体水平永远不会被偏好,但在多水平选择中,满足$\frac{b}{c}>1+\frac{k\theta}{(k-2)\lambda}$时合作就会产生。然而,这一阈值是高于良好混合的组内互动多水平选择的等效阈值$\frac{b}{c}>1+\frac{\theta}{\lambda}$的,这意味着具有生灭更新的图结构实质上通过多水平选择抑制了合作的演化。
除了BD更新,网络结构中,无论是采用灭生更新(DB)还是模仿更新(IM),集体借助多水平选择促进合作的能力都依赖于变量近邻数量$k$。对于生灭更新,当近邻数量$k$足够小($k<\frac{2\lambda}{\theta}$)时,收益-开销比阈值高于良好混合的组内互动多水平选择的等效阈值;当近邻数量$k$足够多时低于这一阈值。而个体水平选择与之相反,收益-开销阈值等于网络度$k$,因此稀疏的网络结构越有利于个体水平选择下的合作。当$k\to\infty$时,DB和IM阈值都接近于基线。这意味着在捐赠博弈(简化的囚徒困境)下,阈值对近邻数量非单调依赖,存在合适的近邻数量使合作最大化。
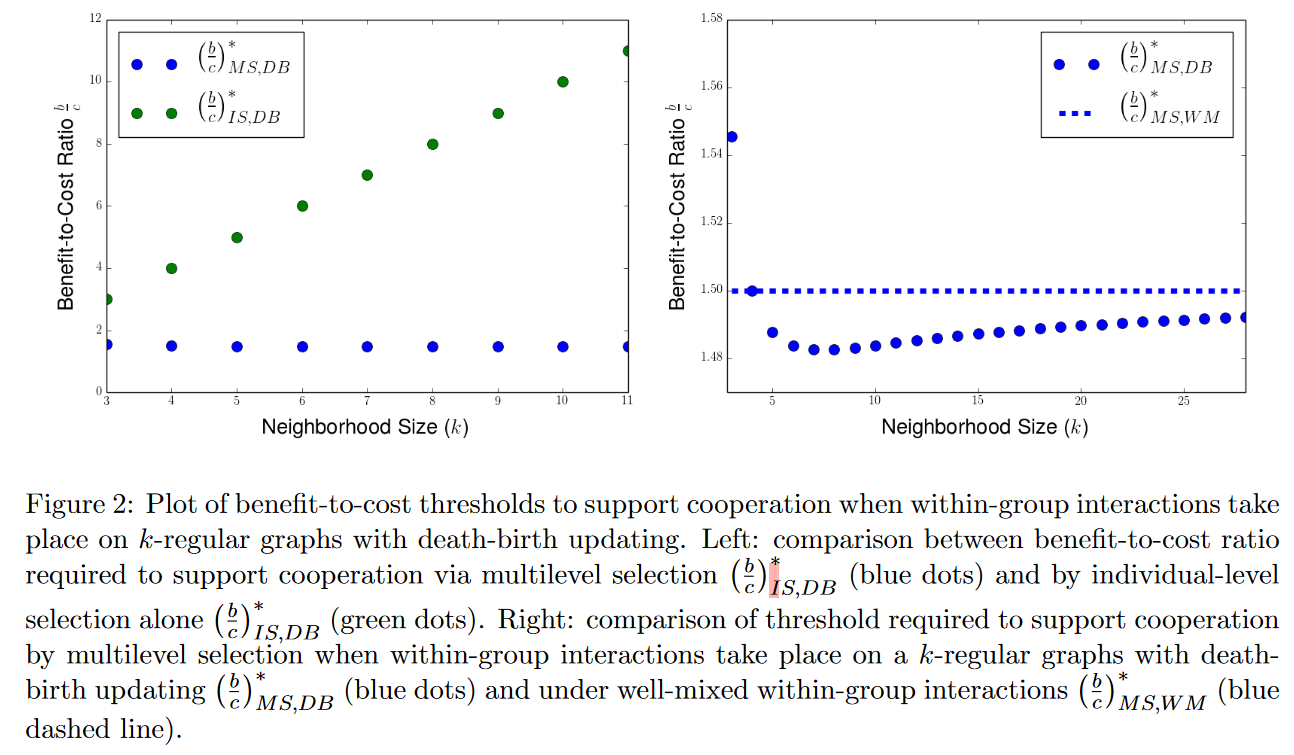
注意横坐标均进行了调整。
具有连续努力水平的模型
为进一步分析个体叛逃动机与集体合作动机的角力,作者研究了一族损益依赖于连续水平的努力的社会困境。
努力水平$e$刻画了合作/叛逃的程度,本模型中当个体施加的努力$e$与给定努力水平$\tilde{e}$的对手互动时,其损益$u(e,\tilde{e})=(a-e)\tilde{e}$。
因此,该博弈在$e^\ast=\frac{a}{2}$时取得集体损益最优,尽管个体博弈时永远不可能达到这一水平。不过,多水平选择有助于接近社会最优。
考虑两个参与者的博弈,努力水平$e_C>e_D$,损益矩阵为$\begin{align}C\\ D\end{align}\begin{pmatrix}e_C(a-e_C)& e_D(a-e_C)\\ e_C(a-e_D)&e_D(a-e_D)\end{pmatrix}$,因此在单一群组中,演化总是导致完全叛逃,产生最低水平损益。如果努力水平是可变且可遗传的,单一群组的演化总是将努力水平将至0。
在多个群组的集体中,完全合作组损益为$G(1)=e_C(a-e_C)$,完全叛逃组损益为$G(0)=e_D(a-e_D)$。在接近完全合作组内,个体合作的损益为$\pi_C(1)=e_C(a-e_C)$,叛逃损益为$\pi_D(1)=e_C(a-e_D)$。
在当前设定下,维持长期合作的选择强度阈值为$\lambda^\ast(e_C,e_D)=\frac{(\pi_D(1)-\pi_C(1))\theta}{G(1)-G(0)}=\frac{e_C\ \theta}{a-e_C-e_D}$,$\lambda^\ast(e_C,e_D)$随$e_C$和$e_D$单增,这意味合作和叛逃的努力水平上升都需要更强的组间选择来支撑长期合作。
这一结果意味着合作努力水平的提升具有两种相反的效果,一方面提升努力水平$e_C$会提升个体叛逃的动机$\pi_D(1)-\pi_C(1)$,特别是组间竞争弱的时候;另一方面当合作努力水平较高时,全合作组的集体产出$G(1)$也会提高,促进合作。
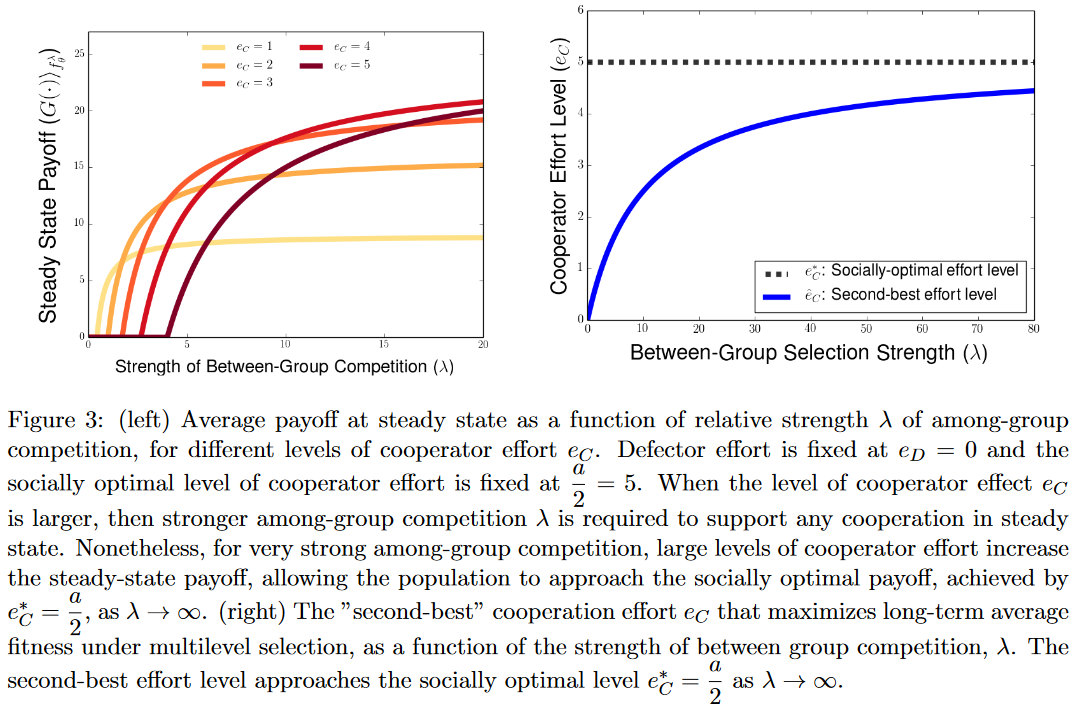
对于$\lambda>\lambda^\ast$,平均损益$\langle G\rangle_{f^\infty}=e_C(a+\frac{\theta}{\lambda}e_D-(1+\frac{\theta}{\lambda})e_C)$,当$\lambda\to\infty$,集体平均损益稳态是$e_C(a-e_C)$,在$e_C=\frac{a}{2}$处取得。但是对于给定的有限$\lambda$,努力水平$\hat{e}_C<\frac{a}{2}$会产生多水平选择下的最大集体损益,这一结果可以被视作动态多水平选择产生的次优解,该点处增加努力水平会同时增加集体合作动机和个体叛逃动机,而次优努力水平提供了二者的最优平衡。
-
D’Souza, R. M., Di Bernardo, M., & Liu, Y.-Y. (2023). Controlling complex networks with complex nodes. Nature Reviews Physics, 5(4), 250–262. https://doi.org/10.1038/s42254-023-00566-3 ↩
-
Cooney, D. B., Levin, S. A., Mori, Y., & Plotkin, J. B. (2023). Evolutionary dynamics within and among competing groups. Proceedings of the National Academy of Sciences, 120(20), e2216186120. https://doi.org/10.1073/pnas.2216186120 ↩
