日常 世界趋势 消费者行为 研究方法 资料

【阅】本周阅读摘选2023-05-22 → 2023-05-28

Posted by Cao Zihang on May 29, 2023 Word Count:
本周阅读摘选
2023-05-22 → 2023-05-28
目录

学术相关

尤瓦尔·赫拉利 演讲：AI不需要意识就可以毁灭人类文明

尤瓦尔·赫拉利认为AI可能是人类遇到的第一种“无机生命”，至少是无机生命代理，而这将彻底改变人类对生态系统的认知。过去人们认为，在AI对人类产生威胁之前，必须达成具有感知力（意识、感知、情感），在物理世界的高效移动能力两个里程碑，而迄今为止，AI的发展远远没有触及这两个里程碑。但是，尤瓦尔挑战了这一观点，他指出目前AI已经进入公共领域，并可能对人类文明产生威胁。

我们已知，开发者难以掌控他们所创造的工具的全部能力，他们经常会被这些工具涌现的能力和品质震惊，这表示着AI的用途可能超越人类的控制范畴，但比起那些非法应用而言，更重要的是新型AI工具正逐渐获得深入人类社会、与人亲密关系的能力。LLMs类AI操纵和生成语言的能力，为这些工具提供了进入所有人类设施的途径——AI破解了人类文明的操作系统，因为之前人类文明所有的设计都基于语言。想象一下，如果生活在由一个熟悉如何以极高效率利用人类思维弱点、偏见和成瘾性的异族智能塑造法律、制度、故事和工具的世界会对人类意味着什么？这是一个宏大的问题，并对人类社会具有颠覆性影响。例如，AI可以逐步深入地操纵人类的观点，通过与成千上万的人建立虚假的亲密关系控制人类的行为，而与之对应的，人类试图说服AI的行为是完全不具有意义的。尤瓦尔声称，这将是人类主导的历史的终结（不是全部历史的终结）。在不久的将来，AI将消耗掉人类所有的历史内容，并开始历史的创造，而根据尤瓦尔的观点，人类从未真正接触过现实，我们总是被文化包裹，并通过文化的棱镜体验现实，在过去这些文化是完全被人类控制的，但如今它被彻底改变了。

尤瓦尔认为这是极其可怕的，但是AI真的会比记者更糟糕吗？严格地说，我们没有任何证据。针对如何应用AI即将引发的文化创造，我们存在着大量的未知，而且，我们当下的算法真的没有参与文化创造吗？

此外，我对于alien或类似的比喻存在着质疑，虽然尤瓦尔解释这只是一个词汇的选择，但我总觉得带有一种西方对陌生事物具有不证自明的恐惧性的感觉，但不知道是否也只是一种文化棱镜的偏见。

整体上来说，这段演讲确实包含了非常有趣且重要的想法。

浙江大学丨推荐奖励计划的非货币奖励与推荐意愿：奖励—产品一致性的作用1

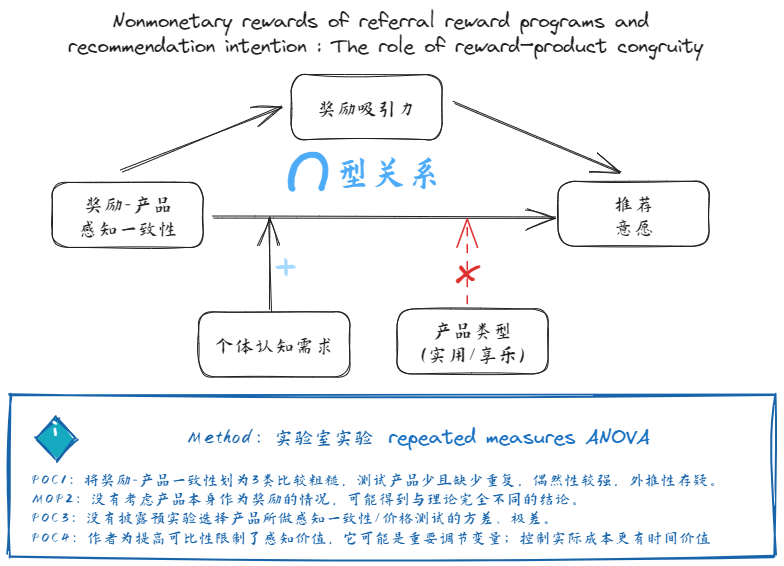
image-20230814165924591

主题 Title Author Journal ROF SPL CPL
推荐奖励计划 Nonmonetary rewards of referral reward programs and recommendation intention: The role of reward–product congruity (Peng, X., Xing, Y., Tian, Y., Fei, M., & Wang, Q.;undefined) Decision Support Systems 线上推荐奖励计划中，中等的奖励-产品一致性容易导致更高的推荐意愿，呈倒U型。感知奖励吸引性为中介变量，个体认知需求为调节变量。实用型/享乐型产品在倒U型关系上存在复杂差异（三因素交互） RRP中非货币奖励的重要性与日俱增，根据契合理论，消费者对奖励-产品一致性强的RRP推荐意愿更高，存在正线性关系 原有研究忽视了图示一致理论，该理论优先考虑模式不一致的作用，认为适度的一致更能导致积极的反应
GAP RFW POC/RPP IV DV Method
目前，在了解非货币奖励特点的影响方面工作较少，大多工作忽视了图示一致理论 1.该研究采用实验室实验方法，缺少真实情境。 2.在产品选择、测量上本研究进行了简化，需要更多重复试验。 3.忽略了消费者的动机。 1.作者将奖励-产品一致性划为3类，本身就比较粗糙，产品选择又不充分，缺少重复，实验可重复性可能较差，偶然性较强。2.没有考虑产品本身作为奖励的情况，可能得到与理论框架完全相反的结论，没有验证或排除。3.没有披露预实验选择产品所做感知一致性/价格测试的方差、极差。4.作者为提高可比性限制了感知价值，但IV-DV关系中感知价值可能是重要调节变量；在实践价值上，控制实际成本更有意义 奖励-产品一致性 推荐意愿 实验室实验，repeated measures ANOVA

CMV四种检验方式 2

之前做过一些量表开发的工作，虽然当时看了一定的教程书局，但实事求是地讲学得一知半解，没有下够功夫，做出的结论觉得有很多问题……特别是统计原理这部分，很多中文论坛上的内容完全忽视掉了这部分，我还是觉得在完全理解统计原理和技术细节之前最好别用结构方程模型，做出来的东西不负责任。等有合适的机会，希望系统地学习一下。

人们对共同方法方差问题及其潜在偏差影响的关注始自Campbell和Fiske在1959开发的多质多法矩阵MTMM，之后随着验证性因子分析的流行，人们发现可以通过额外添加表示共同测量方法的潜变量，分析其与其他潜变量、指标的关系来评估CMV。ULMC是最早的基于CFA技术的CMV测量方法。

目前针对测量CMV的CFA技术主要分类包括（a）数据中不包含假定的CMV来源（亦称未测量的潜方法结构ULMC）（b）包含对一些被假定为CMV来源变量的间接测量（标记变量Marker Variable）或直接测量（测量的原因变量Measured Cause Variable）（c）同时包含多种潜方法变量（混合方法变量模型Hybrid Method Variables Model）。

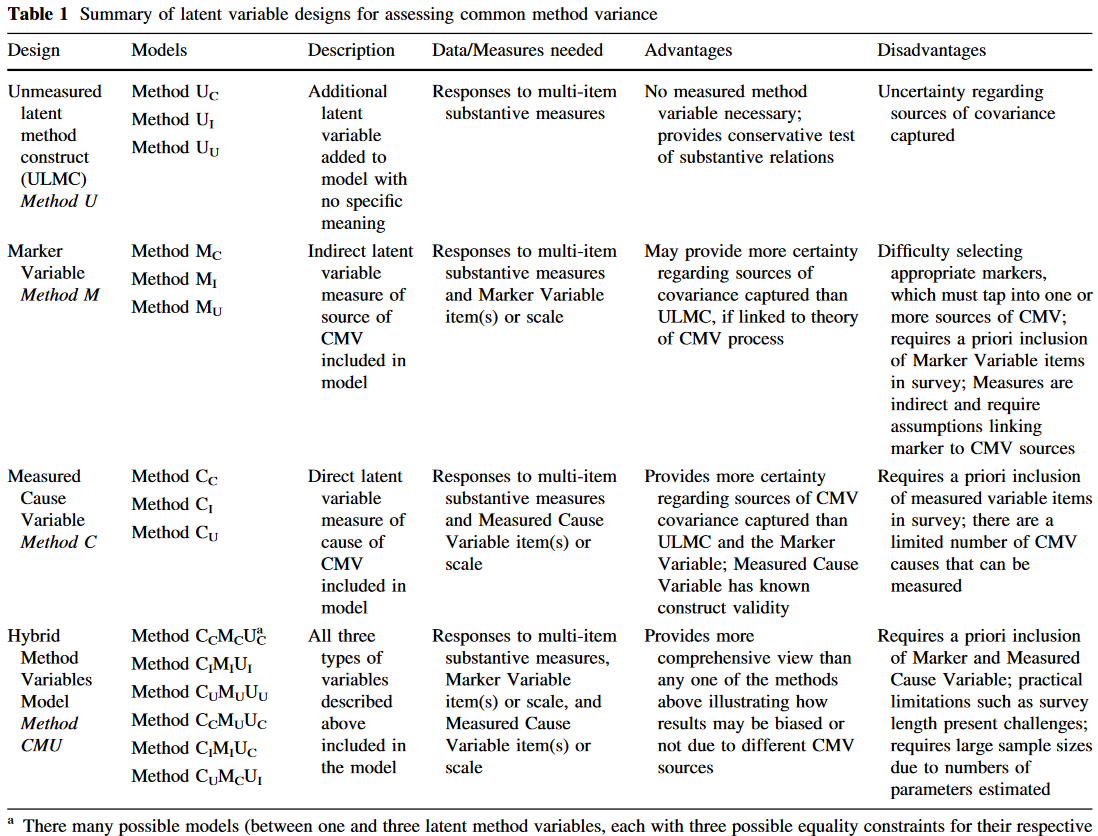
image-20230815121047030

Unmeasured Latent Method Construct

针对含有单一未测量的方法因子的模型，除了方法因子外，它需要潜在变量/因子存在多个指标。Podsakoff认为这类模型控制了单一未测量的潜方法结构的影响。

image-20230815123329802

该方法的问题是模型解释了系统误差效应，但无法识别误差来源，工具、人员、情境和构造都被认为是CMV的成因。因此，ULMC获取的方法因子可能同时包含CMV和其他原因导致的共同方差。例如，该方法没有考虑存在一个或多个多维潜变量的情况，它一些指标残差项的系统性方差可能源于多维实质性差异未被计算导致的，进而高估了CMV。

但是相比于忽视共同方差，错误地归咎为共同方法方差的危害要更小，因此整体上ULMC表现还是良好的。

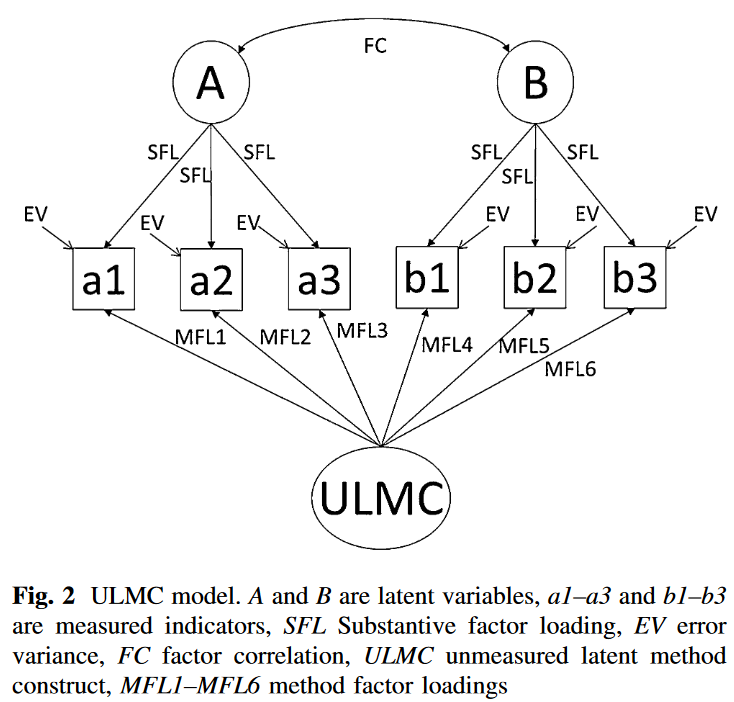
Marker Variables

该方法通过对假定产生CMV的变量进行间接测量，避免了共同方差存在形式的模糊性。Marker Variable最初被定义为与研究中实质的变量不存在理论关联的变量，即Marker Variable与实质变量理论上期望相关性为0。当Maker Variable与其他变量存在非零相关性（意味着存在共同方差），该方法将归因为共同方法方差。

需要注意，Williams（2020）指出如果仅根据是否与实质变量间缺乏关系来选择Marker Variable是不完善的，还应考虑数据中可能存在的具体测量方差。因此，Williams将Marker Variable定义扩展为：“对给定调查相应模型，在一定的实质性待检验变量的测量背景里，捕获或挖掘一种或多种方差来源。”

虽然Marker Variable相比ULMC包含了测量的内容，但它的有效性要取决于Marker Variable与测量理论、CMV来源的关联。

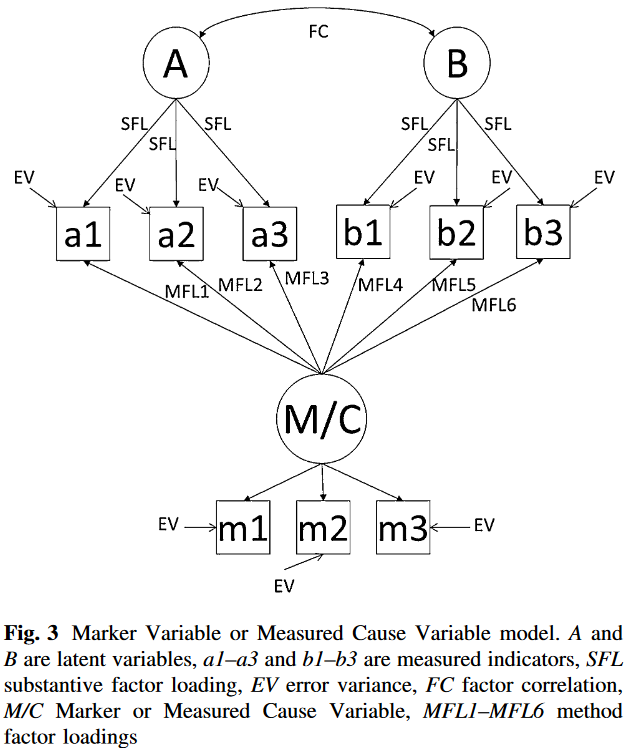
image-20230815142607278

Measured Cause Variables

该方法直接包含方法效应的测量变量——即测量一个或多个被认为是CMV来源或原因的变量。该方法的优势是可以直接通过来源识别评估和控制CMV。然而，可以直接测量的CMV原因是有限的，且没有涵盖所有CMV来源。

该方法与Marker Variables的路径模型是相同的。

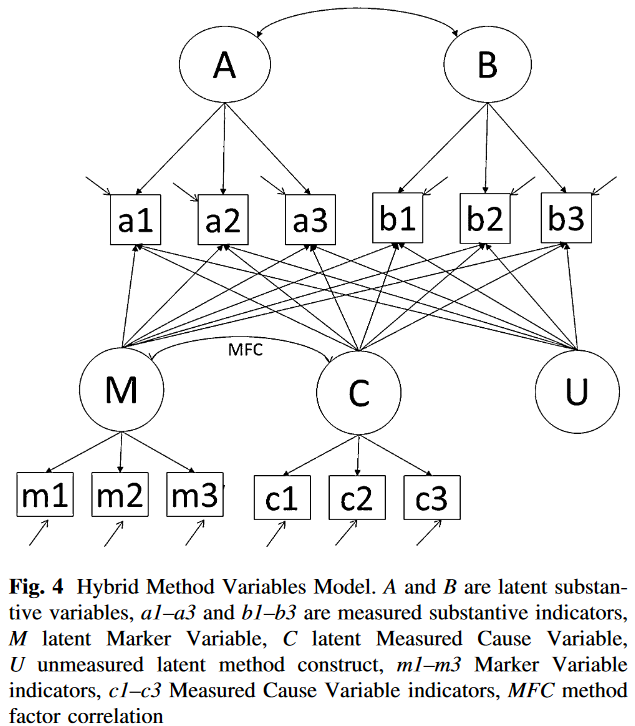
Hybrid Method Variables Model

该模型同时包含Marker、Measured Cause和ULMC三种类型的潜方法变量。这三种潜方法变量与两个实质的潜变量不相关，Marker Variable和Cause Variable之间可以存在方法因子关联，但必须与ULMC无关。

image-20230815222613372

CMV分析流程

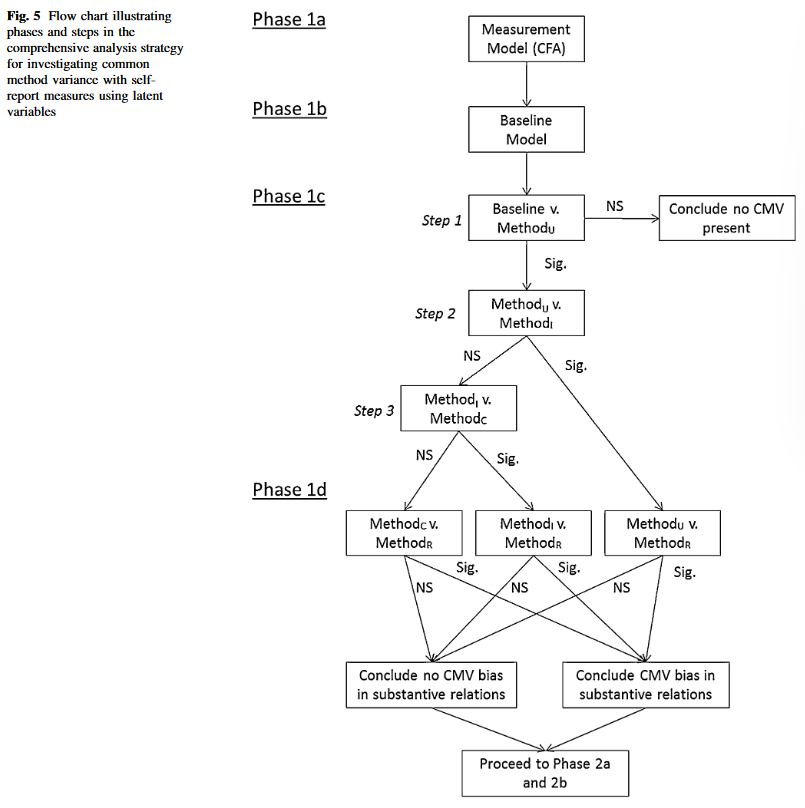
image-20230815232805654

  • Step 1：评估测量模型

本环节的目的是检验连接潜变量与其指标的测量模型，保证潜变量具有充足的区分效度，令潜变量及其指标具有理想的测量属性。

具体地，它要求使用CFA测量模型评估所有潜变量及其指标（如果采用自我报告测量还需控制变量），方法变量及其指标（Marker Variable，Measured Cause Variable）。经验上，所有的分析推荐使用标准化潜变量（因子方差为1）。CFA的评价指标包括卡方、CFI、RMSEA、SRMR在内的所有指标。

如果模型拟合效果较好，需要检验所有潜变量之间的因子相关性，如果任一一对潜变量的相关高于0.8就需要担心其区分效度，分析是否应该删除或合并。

每个指标的信度应该是充足的，即每个指标的$R^2$（squared Multiple Correlation）不低于标准化因子载荷的平方。每个潜变量的组合信度也需要计算，确保它们被多个指标充分表示。

  • Step 2：建立基线模型

本环节的目的是建立一个基线模型用于后续CMV检验。

首先需要明确潜方法变量及其指标的含义。对于Marker Variable和Measured Cause Variable潜方法变量需要通过因子载荷连接它们的指标和实质性潜变量的指标。但是，如果同时自由估计所有的因子载荷，则潜方法变量的含义就成了方法指标和是实质性变量指标的混合体，其含义就模糊了，会损害MFL方法因子载荷的解释性。

幸运的是，该问题可以在检验带有方法因子的全模型之前，通过固定潜方法变量的因子载荷和误差方差解决。若只有一个方法指标，则将之因子载荷固定为1，误差方差为$[(1-指标信度)(指标方差)]$。若其由多个题项组成，则指标信度的估计采用$\alpha系数$。若存在多个方法指标，则需要固定方法指标的多因素载荷和联合误差方差。即在上一环节中对CFA测量模型的每个潜方法变量都保留估计潜方法指标的未标准化因子载荷和误差方差（标准化潜变量，但非标准化指标），作为建立基线模型的固定参数。ULMC方法仅需要向基测量模型添加一个正交的潜方法变量。

其次，三类潜方法变量必须与实质性潜变量正交。基线模型假定所有潜方法变量必须与实质性变量正交。对于混合CMV检验设计，Marker Variable和Measured Cause Method Variable之间允许相关，但必须与实质性变量、ULMC变量正交。

最后，基线模型和测量模型之间没有直接的比较，基线模型由于限制导致拟合较差是正常的，只需要保证初始的CFA测量模型有足够的拟合优度即可。

  • Step 3：方法效应的存在性与等效性检验

本环节需要构建3个模型，即三种添加方法因子载荷（$Method_U$、$Method_I$ 和$Method_C$）的模型，以及使用卡方检验对一组相关的嵌套模型进行比较。混合方法中，潜方法变量类型分别表示为U [ULMC]、M [Marker]、C [Measured Cause]。

$Method_U$、$Method_I$ 和$Method_C$之间的关键区别在于实质性潜变量内部和之间关于方法效应等效性的假设。

①$Method_U$模型包含了在基模型中限制为0的潜方法变量与实质性因子指标之间的方法因子载荷MFLs。角标$_U$指MFLs为“unrestricted”，可以自由估计。$Method_U$通常被用来检验同源方法效应（congeneric method effects）。如果基线模型与$Method_U$存在显著的卡方检验差异，则意味着拒绝MFLs为0的假设，并得出存在不相等的方法效应的初步结论。

②若显著，则继续检验$Method_I$，其中$_I$表示“Intermediate”，指连接实质指标的MFLs在各实质因子之间可以不同，但在各实质因子内部指标的MFLs被限制为相等的。$Method_U$和$Method_I$是嵌套的，因此可以对二者的拟合优度进行卡方检验，就能检验MFLs在因子内部是相等的假设。如果原假设被拒绝，则可以得出存在实质性变量之间存在不相等的方法效应，并使用$Method_U$的结果分析实质性关系之间的方差。如果未被拒绝，则可认为因子内存在相等的方法方差，并需要继续检验$Method_C$。

③角标$_C$表示“constrained”，即所有的MFLs都为限制为相等的，因此该模型是关于非同源性方法效应的检验。在该环节中，$Method_I$和$Method_C$两个模型可以直接比较，检验个实质性潜变量之间是否存在相同的方法效应。对应的零假设为实质性因子内部和之间的方法因子载荷MFLs是相等的。若拒绝了零假设，则保留$Method_I$进入下一步，若没有拒绝则认为实质性潜变量之间和内部存在非同源性方法效应并保留$Method_C$进入下一步。

（为什么相等意味着非同源方法效应？没有查到更多资料）

  • Step 4：在实质性关系中检验共同方法偏差

如果通过基模型与$Method_U$、$Method_I$ 和$Method_C$比较发现CMV存在，则分析的重点将转向为有方法方差控制和无方法方差控制的模型因子相关性是否存在差异（即共同方法偏差是否存在）。

我们需要构建$Method-R$，“R”表示该模型在实质性因子相关性上存在限制。$Method-R$使用基线模型的实质性因子相关性作为Step 3选出模型（$Method_U$、$Method_I$ 和$Method_C$）的潜方法变量固定参数值。通过检验$Method-R$与选出模型，若显著则拒绝两组因子相关性相等的零假设，进而可以得出实质因子相关性中存在共同方法偏差。之后可以每次只限制一个因子相关性来识别具体的偏差。

  • Step 5：量化实质性指标的方法偏差

量化实质性指标和潜变量的CMV非常重要，我们需要将Step 3选中模型中连接每个实质性指标和实质/方法因子的标准化因子载荷平方，并通过平均值/中位数在每个实质性指标或所有实质性指标层次上进行汇总。若包含多个相关的方法潜变量，则应根据最终保留的方法模型对每个方法潜变量单独计算每个指标的方差分配结果。

  • Step 6：量化实质性潜变量的方法偏差

潜变量程序的一个重要优势在于可以估算综合的信度——组合信度，由于需要更少的限制，它被认为优于α系数。Williams et al. 设计了信度分解来描述与特定形式的方法方差相比，组合信度中有多大程度是由实质性方差导致的。它采用类似于指标层次的方式在潜变量层次进行方差分配。

组合信度$R_{tot}=\frac{[sum(因子载荷)^2]}{[sum(因子载荷)^2+sum(误差方差)]}$

实质性信度$R_{sub}=\frac{[sum(实质性因子载荷)^2]}{[sum(实质性因子载荷)]^2+[sum(方法因子载荷)]^2+sum(误差方差)}$

方法信度$R_{meth}=\frac{[sum(方法因子载荷)^2]}{[sum(实质性因子载荷)]^2+[sum(方法因子载荷)]^2+sum(误差方差)}$

如果研究使用了多种相关的潜方法变量，则应该根据CMV来源逐个分解而不在潜方法变量上汇总，否则潜方法变量的内部相关性将无法得到解释。

混合方法模型示例

本示例包含三个实质性变量：工作控制、同事支持和工作卷入度，理论和实证上支持三者之间存在内在关联。作者选择了消极情绪作为Measured Cause Variable，因为它可能影响每一个实质变量的反应，进而导致带有偏差的相关性；作者选择了生活满意度作为Marker Variable，因为它以情绪为基础，但是不直接涉及工作领域的满意度和参与度（我觉得这点是可能被质疑的，换成今天的天气之类的？）。

  • 参与者与数据
    • MTurk
  • 实质性变量测量
    • 工作控制：Decision Latitude Scale
    • 同事支持：Haynes
    • 工作卷入：Utrecht Work Engagement Scale
      • 活力
      • 奉献
      • 投入
      • 【由于各维度之间关联性较强，且所有题项加载在同一潜变量比3个独立潜变量上拟合优度存在明显差异，量表创立者提倡使用单一潜变量方法】
      • 作者通过因子算法Factorial Algorithm使用领域代表性方法Domain Representativeness Approach将3个维度的题项纳入到3个变量包之中
  • 方法变量测量
    • Measured Cause Variable-消极情绪：PANAS Scale
    • Marker Variable-生活满意度：Life Satisfaction Scale

括号中为组合信度。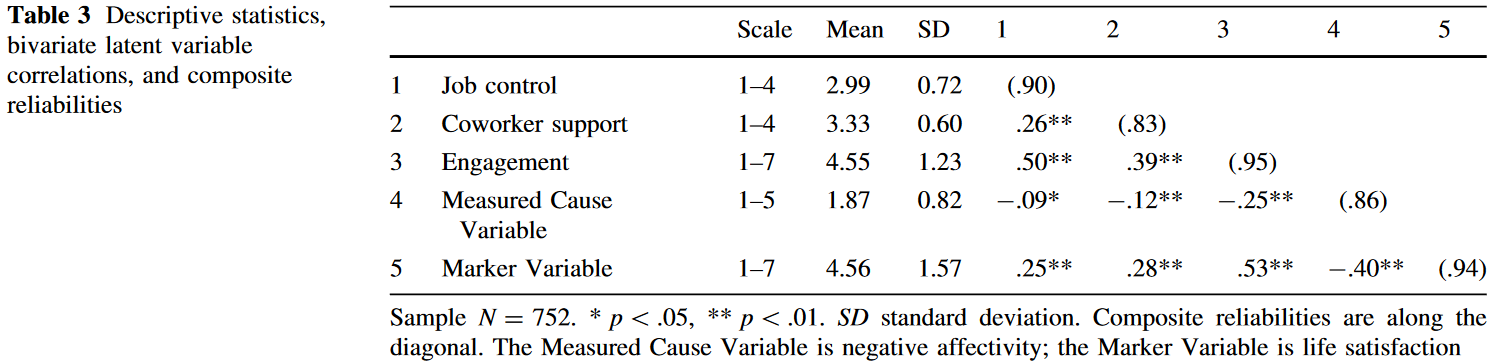image-20230816234523645

  • Step 1：估计测量模型

首先使用实质性变量、Measured Cause Variable（消极情绪）、Marker Variable（生活满意度）。模型的拟合步骤采用Kline（2010）【最新版为第五版3】的指导路线。

$\mathcal{X}^2(142)$ p CFI RMSEA SRMR
390.90 <.001 .976 .048 (.043, .054) .03

因子间相关性均低于0.8，无需担心区分效度。各潜变量对应指标方差解释范围分别为.67-.91（工作控制）、.41-.80（同事支持）、.83-.88（工作卷入）、.46-.66（消极情绪）、.48-.84（生活满意度），均超过0.36。

  • Step 2：建立基线模型

通过固定实质性因子载荷和Measured Cause Variable、Marker Variable的误差方差为Step 1中对应的非标准化值，并限制Measured Cause Variable与实质性变量、Marker Variable与实质性变量之间的相关性为0，构建基线模型。

基线模型的统计指标：（$Table\ 4$)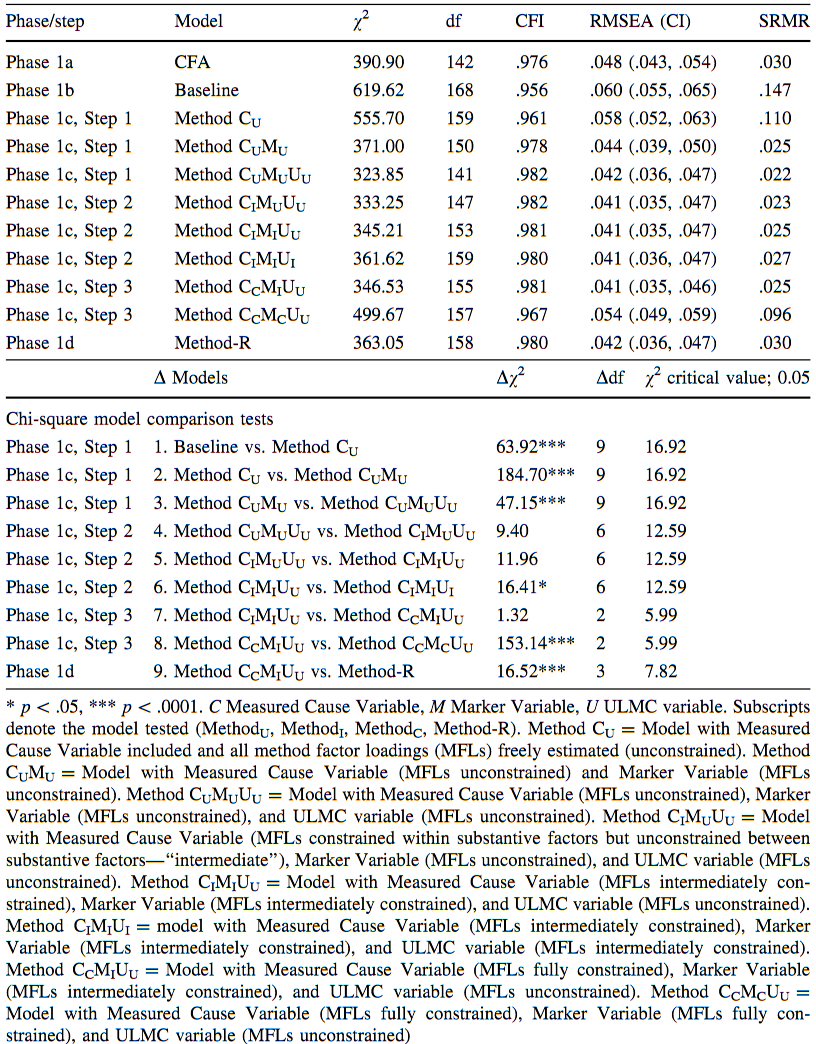image-20230817122424919

基线模型的标准化实质性因子载荷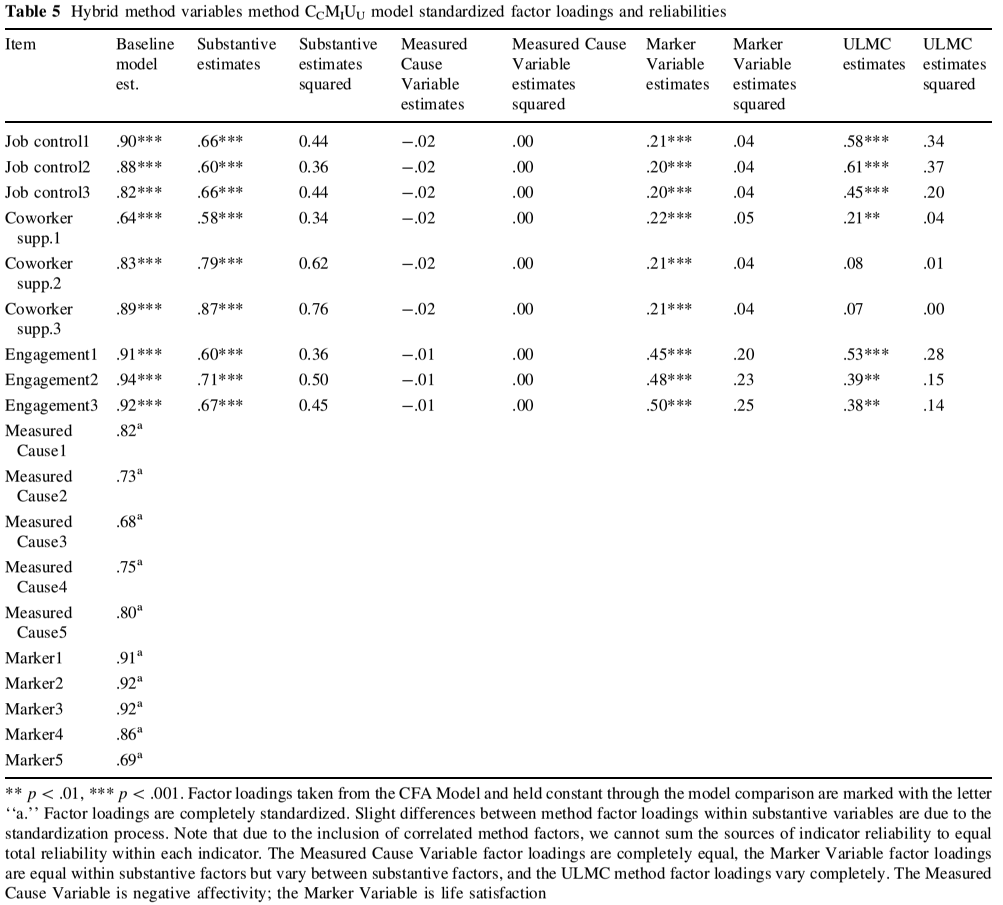：image-20230817131540811

基线模型实质性因子相关性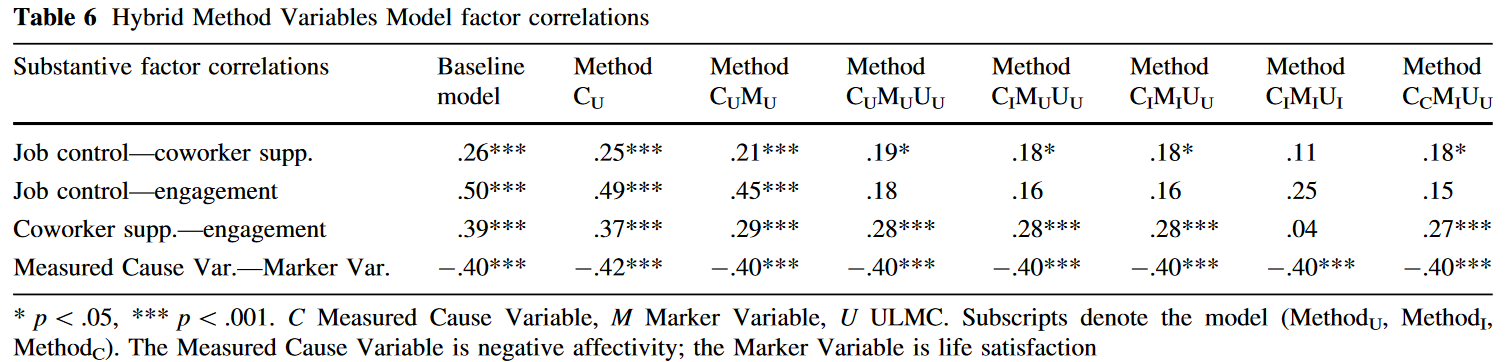：image-20230817132503426

  • Step 3：方法效应的存在性与等效性检验

如$Table\ 6$所示，模型变量输入的顺序会影响因子的相关性。考虑到Measured Cause Variable在了解CMV来源方面具有相对优势，本研究优先输入Measured Cause Variable。

作者首先添加了从Measured Cause Variable指向实质性指标的9个方法因子载荷MFLs，且自由估计它们（见$Table 4$），与基线模型的比较表明$Method\ C_U$具有拟合优势，因此保留$Method\ C_U$，且除了一个MFL外其他MFL均显著。

之后，作者向模型中添加由Marker Variable指向实质性变量的无约束方法因子载荷MFL，模型比较显示$Method\ C_UM_U$模型拟合显著优于$Method\ C_U$，因此保留新模型，此时所有的Measured Cause Variable MFLs不显著，Marker Variable MFLs显著。

继续添加ULMC MFLs，$Method\ C_UM_UU_U$拟合显著优于$Method\ C_UM_U$，此时所有的Marker Variable MFLs显著，7/9 ULMC MFLs显著。至此，结论支持存在方法效应。

向每个实质性因子内部添加相等MFLs的约束，依旧从Measured Cause Variable开始分析，与$Method\ C_UM_UU_U$比较结果显示未能拒绝二者相等的零假设，保留$Method\ C_IM_UU_U$模型。

之后添加与Marker Variable连接的MFLs约束，同样在模型拟合上不存在显著差异，因此保留$Method\ C_IM_IU_U$。

向$Method\ C_IM_IU_U$添加连接ULMC MFLs约束得到$Method\ C_IM_IU_I$，模型，发现相比于$Method\ C_IM_IU_U$存在显著的拟合优度下降，因此拒绝ULMC MFLs相等的约束，保留$Method\ C_IM_IU_U$模型。

接着检验Measured Cause Variable和Marker Variable MFLs是否相等，依次约束二者的MFLs使之在实质性因子内部和之间相等。$Method\ C_CM_IU_U$相比$Method\ C_IM_IU_U$没有显著拟合优度变化，因此不能拒绝实质性因子内部和之间的MFLs相等的原假设，保留$Method\ C_CM_IU_U$。而$Method\ C_CM_CU_U$拟合优度显著差于$Method\ C_CM_IU_U$，因此拒绝Marker Variable在实质性因子内部和之间MFLs相等的假设，保留$Method\ C_CM_IU_U$。

如$Table\ 5$所示，$Method\ C_CM_IU_U$的Measured Cause MFLs较小且不显著；Marker Variable MFLs在实质性因子内部相等，但之间不等；ULMC在实质性因子内部和之间均不等。需要强调，多数ULMC和Marker Variable MFLs是显著的。

  • Step 4：在实质性关系中检验共同方法偏差

约束$Method\ C_CM_IU_U$模型的因子相关性估计为基线模型的估计值（.26, .50, .39替换.18, .15, .27），将$Method-R$与$Method\ C_CM_IU_U$进行比较，发现存在显著拟合优度下降，因此拒绝相关系数不存在差异的假设，得出实质性相关系数存在CMV偏差。

由于两组因子相关性之间的差异模型，及缺乏有关结构路径的实质性假设，作者没有研究其他$Method-R$模型确定具体的偏差情况，但实际研究中应该这样做。

  • Step 5：量化实质性指标的方法偏差

在$Table 5$中，通过计算标准化MFLs平方均值，ULMC解释了17.2%的实质性指标方差，Measured Cause Variable平均解释了0%，Marker Variable解释了10.5%。

  • Step 6：量化实质性潜变量的方法偏差

此处利用$Method\ C_CM_IU_U$模型进行潜变量信度分解，由于它不满足方法因子正交假设，所以不会汇总并评估整体方法信度。

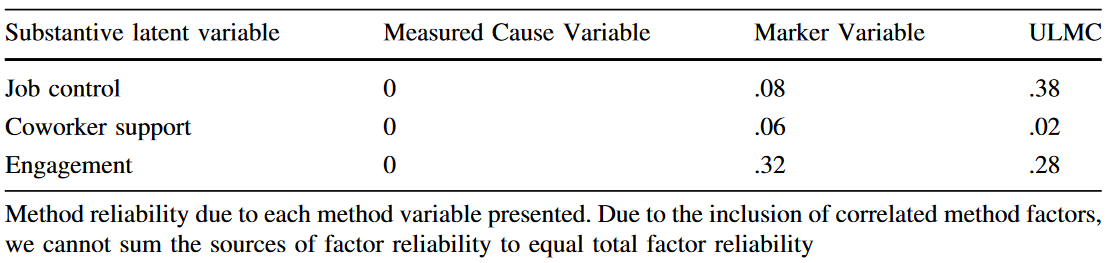
image-20230817175003390

使用注意事项

混合方法存在一些使用限制，例如它必须包含Measured Cause Variable和Marker Variable的相关题项，考虑到估算的参数数量，该方法要求较大的样本量。通常对于最小样本量的建议是自由参数的10~20倍。

作者建议研究人员在实施研究之前就要考虑CMV的可能来源（数据收集测量、研究变量），并在数据收集中添加相关题项。为节约题项，作者建议使用验证过的短量表，如简短的PANAS量表作为测量方法变量。打包法可能有助于处理方法变量指标（但存在争议）。合适的方法变量需要依据研究问题和方法决定。

作者要求读者注意，使用混合方法必须要满足CFA模型的多个统计假设和数据要求。如果研究变量是非正态的，研究者必须对卡方检验进行修正或采用其他的模型差异测量方法。

变量的输入顺序会影响分析的结果，该顺序需要基于概念上的考虑、各类方法变量的相对效果及一些注意事项，作者推荐顺序是Measured Cause Variable、Marker Variable、ULMC，如果同时存在多个Measure Cause Variable或Marker Variable则应该首先纳入认为与CMV来源最相关的变量。若研究者对一个或多个方法变量有特定的假设，则变量的输入顺序就要根据研究任内而定。

如果某个方法变量的无约束MFLs被发现无益于模型改进，那么在后续阶段可能要考虑丢弃。目前是否要对不显著变量进行剪枝尚无定论，需要仔细分析。

在本案例中，作者同时没有基于实质性变量进行划分和检测，但是有些情况下，研究者可以基于实质性变量对MFLs等效性进行非同步测试，但这种做法必须要有理论支撑。

混合研究包含的3种方法无论是混合使用还是独立使用均带有局限性。

ULMC包含的不仅仅是CMV还可能有其他来源的共享方差。虽然ULMC可能导致高估CMV，但它为CMV提供了一种保守的估计。

Marker Variable改善了一定的ULMC局限性，但好的Marker Variable很难找到。仅根据Marker Variable与实质性变量之间缺乏实质性关系来选择是不全面的，如果一个Marker Variable与实质性变量不具有理论关联，但与测量过程的某些环节有弱关联，它就不会共享实质性变量的变量。因此基于Marker Variable声称不具有CMV问题需要格外谨慎。在考虑Marker Variable时需要有明确的选择理由，且至少有一个或多个CMV来源相关。示例中，作者选用生活满意度作为Marker Variable，因为它与工作相关的实质性变量只有间接联系，并且是对情感反应倾向的间接测量，因此它可能包含了实质性共享方差，但存在高估CMV偏差的程度。

Measured Cause Variable为ULMC和Marker Variables同时提供了改进。但是它并没有控制其他CMV来源，所以它对CMV整体影响的评估是初步的。在选取Measured Cause Variable时需要谨慎。

CMV偏差结果处理

如果没有CMV偏差存在的证据，则后续的模型检验中无需再包含方法变量。如果存在CMV偏差，一种选择是将识别的方法变量纳入结构模型的估计中，但是在一个包含外生和内生潜变量和指标的模型中，由于要估计的MFL较多，所以可能存在估计困难。一些策略包括使用MFLs和其他变量的初始值；提出所有不重要的MFLs和/或将MFLs和误差方差固定为最终保留模型的值。

CMV研究结果汇报

由于CMV分析的结果通常被要求精简以缩小篇幅，作者提供了一些汇报建议。

作者示例使用的数据源自作者的论文4

清华大学建筑学院：中国未来人口分布情境分析

项目日期：2019.08.01 ~ 2020.05.31

范畴：低碳城市

尺度：公里网格尺度

  • 以线性回归为核心的市辖区层级人口总量与城镇化率预测
  • 以土地利用变化和LandScan人口耦合数据为核心的公里网格尺度的人口判定

相关研究

国家人口总量研究

空间人口网格分布研究

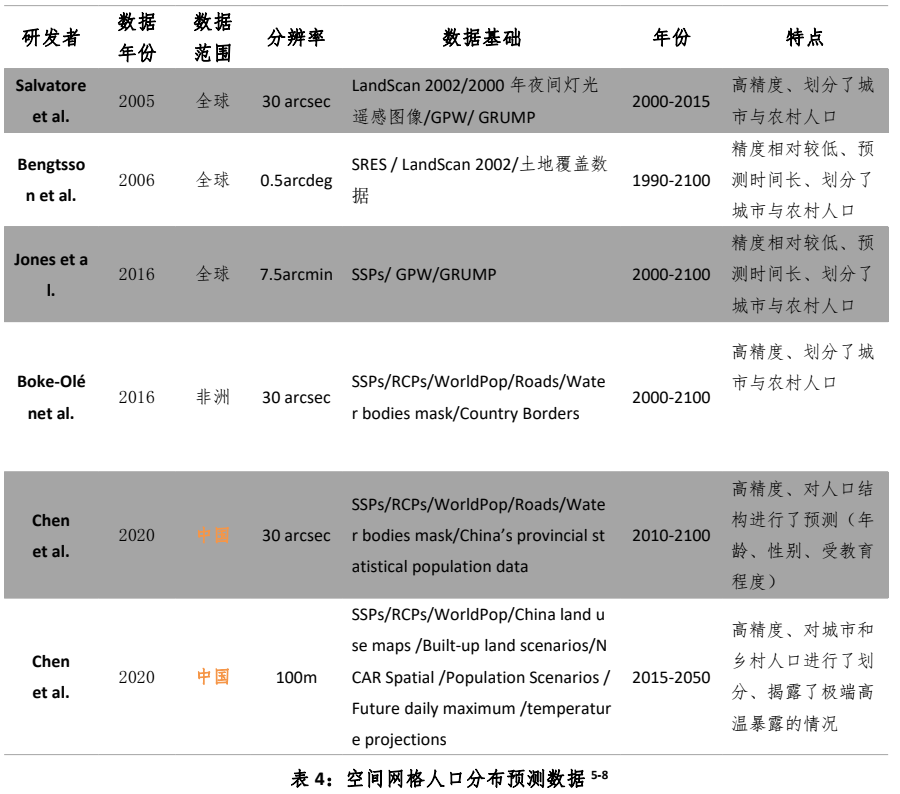
image-20230809233221527

数据与方法

  • 研究范围

大陆地区选择shapefile城市边界数据，包含大陆31个省级行政区、339个地级行政区、2853个县级行政区。

港澳台单独统计。

具体研究感觉有些粗糙，不再赘述。

经济学论文代码复现数据库

  1. Peng, X., Xing, Y., Tian, Y., Fei, M., & Wang, Q. (2023). Nonmonetary rewards of referral reward programs and recommendation intention: The role of reward–product congruity. Decision Support Systems, 113999. https://doi.org/10.1016/j.dss.2023.113999 ↩

  2. Williams, L. J., & McGonagle, A. K. (2016). Four Research Designs and a Comprehensive Analysis Strategy for Investigating Common Method Variance with Self-Report Measures Using Latent Variables. Journal of Business and Psychology, 31(3), 339–359. https://doi.org/10.1007/s10869-015-9422-9 ↩

  3. Kline, R. B. (2023). Principles and practice of structural equation modeling (Fifth edition). The Guilford Press. ↩

  4. McGonagle, A. K., Fisher, G. G., Barnes-Farrell, J. L., & Grosch, J. W. (2015). Individual and work factors related to perceived work ability and labor force outcomes. The Journal of Applied Psychology, 100(2), 376–398. https://doi.org/10.1037/a0037974 ↩

CATALOG
    FEATURED TAGS
    消费者行为 日常 深度学习 学习笔记 可视化 数智化营销 复杂科学 市场调研 研究方法 世界趋势 仿真与决策 日常工具 LLMs 数据科学 机器学习 资料 AB测试 供应链管理 城市科学 推荐系统